关键词:钩端螺旋体病;周期性流行;周期图法
【摘要 】 目的 了解钩端螺旋体病(钩体病)发病周期性规律。方法 采用周期图法分析了宜昌市1960~1997年钩体病疫情资料。结果 宜昌市38年来钩体病年发病率为15.43/10万,流行周期为10年,周期振动有统计学上显著性意义(J=4.179,P<0.05)。结论 这为掌握钩体病流行规律,有效控制疫情提供依据。
Demonstration for periodicity ofleptospirosis in Yichang City of Hubei Province during 1960-1997
CHENG Deming and PAN Huiming.
Yichang City Health and Anti-epidemic Station,Yichang,Hubei Province 443000
【Abstract 】 Objective Tostudy the periodicity of leptospirosis incidence. Methods Data ofleptospirosis epidemics in Yichang City collected during the past 38 years from 1960 to1997 were analyzed with periodic graphics method. Results Cause-specificincidence rate of leptospirosis was 15.43 per 100 000 in average, with an epidemicinterval of 10 years, with statistical significance in periodic vibration (J=4.179,P<0.05).Conclusion The results mentioned above provided scientific basis forthe effective control and prevention of the disease.
【Key words 】 Leptospirosis Periodicity Periodicgraphics
钩端螺旋体病(钩体病)是宜昌市重要的自然疫源性疾病之一,流行近40年。经多年的调查,已基本摸清该病的流行规律,现采用周期图法[1] ,从理论上作进一步论证。
资料与方法
疫情资料由宜昌市卫生防疫站提供(表1)。采用的分析方法是周期图法。
表1 宜昌市38年钩体病发病率
| 时间(年) | 发病率(/10万) | 时间(年) | 发病率(/10万) |
| 1 | 2.15 | 20 | 2.58 |
| 2 | 0.46 | 21 | 1.72 |
| 3 | 7.15 | 22 | 2.30 |
| 4 | 19.67 | 23 | 13.17 |
| 5 | 12.25 | 24 | 101.30 |
| 6 | 10.83 | 25 | 11.57 |
| 7 | 5.07 | 26 | 4.81 |
| 8 | 1.30 | 27 | 3.10 |
| 9 | 0 | 28 | 2.39 |
| 10 | 0.69 | 29 | 1.57 |
| 11 | 7.29 | 30 | 1.02 |
| 12 | 5.78 | 31 | 1.30 |
| 13 | 5.86 | 32 | 1.18 |
| 14 | 198.90 | 33 | 1.18 |
| 15 | 70.72 | 34 | 4.09 |
| 16 | 21.40 | 35 | 2.02 |
| 17 | 8.96 | 36 | 6.99 |
| 18 | 24.92 | 37 | 15.05 |
| 19 | 4.88 | 38 | 5.88 |
设对具有相等时间间隔的周期函数:

把其展开成傅里叶级数,其一阶偕波傅氏系数为:
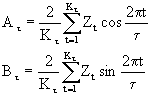
式中K为序列长度n所包含的整数倍,τ为试验周期,Zt 为序列每项数值。为了确定序列的真正周期,令S2 τ =A2 τ +B2 τ ,用不同的τ进行试验,取使S2 τ 达极大值时的τ作为序列周期t,并作显著性检验。
结果
一、隐含周期的计算:由于序列时间长度为38年,因而取试验周期τ=2,3,……,19,S2 τ 计算值见表2。由表2可见τ=10时,S2 10 =709.04达极大值,即隐含周期为10年。
表2 宜昌市38年钩体病隐含周期
| τ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| K | 19 | 12 | 9 | 7 | 6 | 5 | 4 | 4 | 3 |
| Aτ | 12.71 | 3.71 | -4.75 | 8.66 | -1.38 | -3.71 | 8.99 | -15.22 | -24.44 |
| Bτ | 0 | -8.37 | -3.86 | -1.34 | 6.97 | -4.08 | -14.34 | -13.73 | 10.57 |
| Sτ | 161.54 | 70.06 | 51.23 | 76.79 | 50.49 | 30.41 | 286.46 | 420.16 | 709.04 |
| τ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| K | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Aτ | -5.43 | 9.20 | 19.04 | 16.39 | 11.34 | 7.09 | 4.47 | 2.95 | 2.54 |
| Bτ | 22.18 | 15.90 | 9.10 | -1.05 | -5.87 | -7.32 | -7.37 | -7.25 | -7.53 |
| Sτ | 521.44 | 337.45 | 445.33 | 269.73 | 163.05 | 103.85 | 74.30 | 61.27 | 63.15 |
二、检验S2 10 是周期振动的极大值:因钩体病发病率方差σ2 =1272.59,并将有关数据代入假设检验统计量公式计算:

根据表3界值,得J>J0.05 =2.996,故P<0.05,拒绝“无周期振动”的假设,即可认为该发病率序列存在周期性。
表3 周期振动显著性检验界值
| α | 0.01 | 0.05 | 0.10 | 0.20 | 0.50 |
| Jα | 4.605 | 2.996 | 2.303 | 1.609 | 0.693 |
讨论
用周期图法分析宜昌市钩体病发病规律,论证其发病具有周期性,周期为10年,这一结论与国内有关报道一致[2,3] 。据疫情资料,宜昌市自1960年开始有钩体病例报告,从1960~1997年共发病19526例,年平均发病率为15.43/10万,其间共有4次流行高峰,每次高峰间隔大约为10年,由于人为有效措施,从70年代开始,每次流行高峰的峰值呈下降趋势。认清钩体病的周期性流行规律,有利于科学制定相应的预防措施,进而能有效地控制疫情。
参考文献
1 戴胜利,童身以.周期图法在疾病监测中的应用.中国卫生统计,1988,5∶45-46.
2 潘会明.宜昌地区钩端螺旋体病的流行特点.中国公共卫生,1986,5∶33.
3 何浙生,蒋建国,柴曼君.钩端螺旋体病.见:耿贯一,主编.流行病学.北京:人民卫生出版社,1980.317-330.
(收稿:1999-03-15 修回:1999-06-17) , http://www.100md.com