晶状体折射率非均匀性特点消除球差的作用机制
作者:毕会英 贺国珠 孔德兰
单位:毕会英 贺国珠 (新乡医学院 物理教研室);孔德兰 (新乡医学院 三附院,河南 新乡 453003)
关键词:折射;折射率;球差;晶状体
中国医学物理学杂志990209 摘要:本文以光的折射定律为基础,建立了非近轴光线单球面折射成像的精确公式,讨论了非近轴光线经单球面折射、透镜折射成像的球差,分析了晶状体中央区折射率较高这一特点能消除球差的作用机制,给出了平行光线经角膜、晶状体后像的位置和无球差情况对晶状体折射率数值的要求。
中图分类号:R318.52
文献标识码:A
文章编号:1005:202X(1999)02-0086-03
, 百拇医药
The working mechanism of non-evenness of crystal index of
refraction against spherical aberration
BI Hui-ying1, HE Guo-zhu1,KONG De-lan2
(Department of Physics;2.The third Affiliated Hospital,Xinxiang Medical College, Henan 453003,China)
Abstract:Based on the law of refraction of light,An accurate formulate of single-spherical refraction of non-paraxial light ray was established.Discussions were made on non-paraxial light ray through single-spherical refraction and the spherical aberration of the refraction image of lens.Another discussion was about the high index of refraction in the crystal centre which contracts with the spherical aberration.The position of parallel light through corner and crystal back image was given and so were the requirements of non-spherical aberration towards the crystal index of refraction.
, 百拇医药
Key words:refraction;index of refraction;spherical aberration;crystal body
引言:非近轴光线经光学系统后不再聚于一点,即产生了球差。如何减少球差或消除球差是研究、制造摄像机镜头、放映机镜头等光学系统很重要且复杂的工作,通常是采用多个透镜组合的办法达到减少球差的目的。晶状体中央区折射率较高有利于消除球差,这种现象无法利用近轴光线的单球面折射成像公式解释。本文成功解释了引起这种现象的机制,这对研究晶状体变性所引起的视力衰退、人工晶状体的研制具有指导意义。
1 非近轴光线的单球面折射
如图1,两媒质折射率为n1、n2,分界面曲率半径r,入射光线和主光轴夹角为θ、与分界面交于p点,p点距主光轴距离为h,分析物距u、像距v的关系两边同时除以cosθ cosi cos β得
, 百拇医药
由折射定律:n1 sin α=n2 sin Φ (1)
α=θ+i Φ=i-β n1 sin(θ+i)=n2 sin(i-β)
n1 sinθ cosi+n1cosθ sini=n2 sini cosβ-n2 cosi sinβ (2)
(2)
在△OPH、△CPH、△IPH中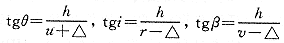
且
, 百拇医药
代入(2)式化简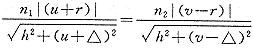 (3)
(3)
式中 (4)
(4)
图1 非近轴光线单球面折射
(3)式即为非近轴光线单球面折射成像的精确公式。
△亦遵循符号规则:入射光线对着凸球面△取正值,入射光线对着凹球面△取负值。h和△共同规定了非近轴光线的具体情况。
2 非近轴光线的球差
由(3)式可以详细分析非近轴光线经光学系统后的球差。
, 百拇医药
2.1 非近轴光线单球面折射球差
如图2,设主光轴上一物点(u=300 mm),发出的两条光线和折射球面(曲率半径r=10 mm,n1=1.336,n2=1.386)交于p、p′两点,两点距主光轴距离h=4 mm、h′=2 mm,分析两折射光线和主光轴的交点I、I′的位置或像距v、v′差别,由(4)式得出: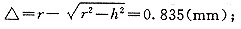

将n1、n2、r、u、h、△、h′、△′分别代入(3)式可得出
v=1350 mm v′=2114 mm
两像点相距764 mm,球差很大。
, 百拇医药
图2 非近轴光线单球面折射的球差
2.2 非近轴光线经折射率均匀透镜后的球差(模拟晶状体折射率均匀情况)
如图3,设透镜前后曲率半径为r1=10 mm、r2=-6 mm,透镜两顶点间厚度l=3.6 mm,透镜的折射率为n2=1.386,媒质的折射率n1=1.336,分析2.1中两入射光线经透镜后折射光线和主光轴的交汇点位置的变化。对于第一折射面,自物点发出的光线(图中虚线)应和2.1的结果一样。所以,v1=1350 mm,v1′=2114 mm。对于第二折射面
u2=-(v1-l)=-(1350-3.6)=-1346.4(mm)
u2′=-(v′1-l)=-(2114-3.6)=-2110.4(mm)
, 百拇医药
在△IPH中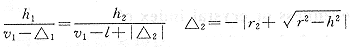
将h1、v1、△、r2代入(4)式得
h2≈4 mm △2≈-1.527 mm
同理 h′2≈2 mm △′2≈-0.343 mm
代入(3)式得v2≈106 mm v′2≈140 mm
图3 非近轴光线经透镜折射后的球差
, http://www.100md.com
经过折射率均匀的模拟晶状体后,来自300 mm处的物点的像相距34 mm,仍有较大的球差。
3 非近轴光线经过晶状体后的球差
3.1 u=300 mm物点经晶状体后的像
为了使问题简化,我们假设晶状体内折射率沿光轴方向相等,由边缘到中央呈线性增长(如图4)。若边缘处h=4 mm时晶状体折射率为n=1.386,中央h=0 mm处n=1.406,可求得h=2 mm时,n′=1.396,晶状体前后曲率半径为r1=10 mm,r2=6 mm[1]。
分析两光线经过晶状体的成像情况。
(1)光线经过晶状体前面
h=4 mm时,和2.1结果一样 v1=1350 mm
, 百拇医药
h′=2 mm时,由(3)式得出v1′=833 mm
(2)光线经过晶状体后面
h=4 mm时,由2.2知 v2=106 mm
h′=2 mm时,由(3)式得出v2′=108 mm
图4 晶状体折射率由边缘向中央线性增大
经过折射率由边缘到中央呈线性增长的晶状体后,两像点相距只有2 mm,h=4 mm、2 mm的两束光线的球差基本被消除。
3.2 平行光线经角膜、房水、晶状体、玻璃体后无球差情况对晶状体折射率的要求
, http://www.100md.com
如图5,眼睛是一较复杂的光学系统,达到晶状体之前首先要经过角膜前面、后面的折射,对于晶状体前面来说,通常情况下相当于-20 mm~30 mm的物点发出的光线[2]。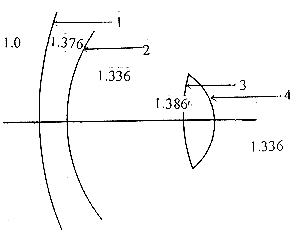
图5 眼睛光学系统折射面
(1)平行光线经过角膜、均匀晶状体后的情况
取角膜的折射率n=1.376,前面曲率半径为7.8 mm,后面曲率半径为6.8 mm;房水的折射率为1.336;晶状体的前、后面曲率半径为10 mm、-6 mm,折射率为1.386 mm,厚度3.6 mm[3]。平行光线进入该系统后经各折射面后的像距如表1。
表1 平行光线经折射率均匀晶状体后的像(mm) h
, 百拇医药
角膜前面
角膜后面
晶状体前面
晶状体后面
4
26.4437
21.5440
17.1852
10.6095
3.5
26.9596
22.0724
17.9261
, http://www.100md.com
11.7178
3.0
27.3942
22.7212
18.5129
12.5247
2.5
27.7536
23.2358
18.9765
13.1332
2.0
, 百拇医药 28.0424
23.6373
18.3372
13.5139
1.5
28.2683
23.9389
19.6076
13.9311
1.0
28.4204
24.1491
, 百拇医药 19.7957
14.1634
表2为 u=250 mm(明视距离)处的物体发出的光线在各折射率面处发生折射后像的情况。 表2 明视距离物体经折射率均匀晶状体后的像(mm) h
角膜前面
角膜后面
晶状体前面
晶状体后面
4
28.3287
20.3569
16.3609
, 百拇医药
9.9772
3.5
29.0059
21.2827
17.2077
11.1612
3.0
29.5815
22.0298
17.8870
12.0352
2.5
, 百拇医药 30.0609
22.6304
18.4306
12.7030
2.0
30.4485
23.1042
18.8579
13.2130
1.5
30.7471
23.4630
, http://www.100md.com 19.1806
13.5910
1.0
30.9590
23.7146
19.4065
13.8525
由表1、表2可清楚看到,外来光线进入眼睛后,若晶状体的折射率均匀,则h=4 mm、1mm的光线在视网膜前成的像有较大的球差,影响术眼视力的提高。
(2)消除球差对晶状体折射率的要求
若只改变晶状体的折射率,其它各部位的光学参数都不变,以平行光线为例,消除球差需晶状体折射率分布如表3所示。 表3 消除平行光线球差对晶状体折射率的要求(mm) h
, 百拇医药
n
v
4
1.386
10.6095
3.5
1.409
10.5843
3.0
1.430
10.5862
2.5
1.448
, 百拇医药
10.6136
2.0
1.468
10.6423
1.5
1.477
10.6091
1.0
1.487
10.5939
根据表3得曲线如图6所示。图6显示,晶状体的折射率由边缘向中央呈线性增长,基本上能消除大量近轴光线在视网膜前的球差。
, 百拇医药
图6 消除平行光线球差对晶状体折射率的要求
4 讨论
(1)公式(4)中,当h r时,△→0;(3)式则转化为人们所熟知的近轴光线的单球面折射公式n1/u+n2/v=n2-n1/r说明(3)式是适用于非近轴光线和近轴光线的单球面折射成像的精确公式。
r时,△→0;(3)式则转化为人们所熟知的近轴光线的单球面折射公式n1/u+n2/v=n2-n1/r说明(3)式是适用于非近轴光线和近轴光线的单球面折射成像的精确公式。
(2)为了简明问题解析过程,没有考虑晶状体改变曲率半径因素的影响。
(3)非近轴光线单球面折射成像公式可以解释晶状体消除球差的机理。其结果为人工晶状体制造提供了依据。
参考文献
[1] 刘普和,等.医学物理学[M].北京:人民卫生出版社,1988.
[2] V.B蒙卡斯尔.医学生理学[M].科学出版社,1988.
[3] 张承芬,徐国祥.激光眼科学[M].广东:广东科技出版社,1994.
收稿日期:1998-07-06, http://www.100md.com
单位:毕会英 贺国珠 (新乡医学院 物理教研室);孔德兰 (新乡医学院 三附院,河南 新乡 453003)
关键词:折射;折射率;球差;晶状体
中国医学物理学杂志990209 摘要:本文以光的折射定律为基础,建立了非近轴光线单球面折射成像的精确公式,讨论了非近轴光线经单球面折射、透镜折射成像的球差,分析了晶状体中央区折射率较高这一特点能消除球差的作用机制,给出了平行光线经角膜、晶状体后像的位置和无球差情况对晶状体折射率数值的要求。
中图分类号:R318.52
文献标识码:A
文章编号:1005:202X(1999)02-0086-03
, 百拇医药
The working mechanism of non-evenness of crystal index of
refraction against spherical aberration
BI Hui-ying1, HE Guo-zhu1,KONG De-lan2
(Department of Physics;2.The third Affiliated Hospital,Xinxiang Medical College, Henan 453003,China)
Abstract:Based on the law of refraction of light,An accurate formulate of single-spherical refraction of non-paraxial light ray was established.Discussions were made on non-paraxial light ray through single-spherical refraction and the spherical aberration of the refraction image of lens.Another discussion was about the high index of refraction in the crystal centre which contracts with the spherical aberration.The position of parallel light through corner and crystal back image was given and so were the requirements of non-spherical aberration towards the crystal index of refraction.
, 百拇医药
Key words:refraction;index of refraction;spherical aberration;crystal body
引言:非近轴光线经光学系统后不再聚于一点,即产生了球差。如何减少球差或消除球差是研究、制造摄像机镜头、放映机镜头等光学系统很重要且复杂的工作,通常是采用多个透镜组合的办法达到减少球差的目的。晶状体中央区折射率较高有利于消除球差,这种现象无法利用近轴光线的单球面折射成像公式解释。本文成功解释了引起这种现象的机制,这对研究晶状体变性所引起的视力衰退、人工晶状体的研制具有指导意义。
1 非近轴光线的单球面折射
如图1,两媒质折射率为n1、n2,分界面曲率半径r,入射光线和主光轴夹角为θ、与分界面交于p点,p点距主光轴距离为h,分析物距u、像距v的关系两边同时除以cosθ cosi cos β得
, 百拇医药
由折射定律:n1 sin α=n2 sin Φ (1)
α=θ+i Φ=i-β n1 sin(θ+i)=n2 sin(i-β)
n1 sinθ cosi+n1cosθ sini=n2 sini cosβ-n2 cosi sinβ
 (2)
(2)在△OPH、△CPH、△IPH中
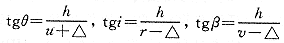
且

, 百拇医药
代入(2)式化简
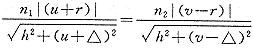 (3)
(3)式中
 (4)
(4)
图1 非近轴光线单球面折射
(3)式即为非近轴光线单球面折射成像的精确公式。
△亦遵循符号规则:入射光线对着凸球面△取正值,入射光线对着凹球面△取负值。h和△共同规定了非近轴光线的具体情况。
2 非近轴光线的球差
由(3)式可以详细分析非近轴光线经光学系统后的球差。
, 百拇医药
2.1 非近轴光线单球面折射球差
如图2,设主光轴上一物点(u=300 mm),发出的两条光线和折射球面(曲率半径r=10 mm,n1=1.336,n2=1.386)交于p、p′两点,两点距主光轴距离h=4 mm、h′=2 mm,分析两折射光线和主光轴的交点I、I′的位置或像距v、v′差别,由(4)式得出:
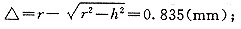

将n1、n2、r、u、h、△、h′、△′分别代入(3)式可得出
v=1350 mm v′=2114 mm
两像点相距764 mm,球差很大。

, 百拇医药
图2 非近轴光线单球面折射的球差
2.2 非近轴光线经折射率均匀透镜后的球差(模拟晶状体折射率均匀情况)
如图3,设透镜前后曲率半径为r1=10 mm、r2=-6 mm,透镜两顶点间厚度l=3.6 mm,透镜的折射率为n2=1.386,媒质的折射率n1=1.336,分析2.1中两入射光线经透镜后折射光线和主光轴的交汇点位置的变化。对于第一折射面,自物点发出的光线(图中虚线)应和2.1的结果一样。所以,v1=1350 mm,v1′=2114 mm。对于第二折射面
u2=-(v1-l)=-(1350-3.6)=-1346.4(mm)
u2′=-(v′1-l)=-(2114-3.6)=-2110.4(mm)
, 百拇医药
在△IPH中
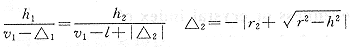
将h1、v1、△、r2代入(4)式得
h2≈4 mm △2≈-1.527 mm
同理 h′2≈2 mm △′2≈-0.343 mm
代入(3)式得v2≈106 mm v′2≈140 mm

图3 非近轴光线经透镜折射后的球差
, http://www.100md.com
经过折射率均匀的模拟晶状体后,来自300 mm处的物点的像相距34 mm,仍有较大的球差。
3 非近轴光线经过晶状体后的球差
3.1 u=300 mm物点经晶状体后的像
为了使问题简化,我们假设晶状体内折射率沿光轴方向相等,由边缘到中央呈线性增长(如图4)。若边缘处h=4 mm时晶状体折射率为n=1.386,中央h=0 mm处n=1.406,可求得h=2 mm时,n′=1.396,晶状体前后曲率半径为r1=10 mm,r2=6 mm[1]。
分析两光线经过晶状体的成像情况。
(1)光线经过晶状体前面
h=4 mm时,和2.1结果一样 v1=1350 mm
, 百拇医药
h′=2 mm时,由(3)式得出v1′=833 mm
(2)光线经过晶状体后面
h=4 mm时,由2.2知 v2=106 mm
h′=2 mm时,由(3)式得出v2′=108 mm

图4 晶状体折射率由边缘向中央线性增大
经过折射率由边缘到中央呈线性增长的晶状体后,两像点相距只有2 mm,h=4 mm、2 mm的两束光线的球差基本被消除。
3.2 平行光线经角膜、房水、晶状体、玻璃体后无球差情况对晶状体折射率的要求
, http://www.100md.com
如图5,眼睛是一较复杂的光学系统,达到晶状体之前首先要经过角膜前面、后面的折射,对于晶状体前面来说,通常情况下相当于-20 mm~30 mm的物点发出的光线[2]。

图5 眼睛光学系统折射面
(1)平行光线经过角膜、均匀晶状体后的情况
取角膜的折射率n=1.376,前面曲率半径为7.8 mm,后面曲率半径为6.8 mm;房水的折射率为1.336;晶状体的前、后面曲率半径为10 mm、-6 mm,折射率为1.386 mm,厚度3.6 mm[3]。平行光线进入该系统后经各折射面后的像距如表1。
表1 平行光线经折射率均匀晶状体后的像(mm) h
, 百拇医药
角膜前面
角膜后面
晶状体前面
晶状体后面
4
26.4437
21.5440
17.1852
10.6095
3.5
26.9596
22.0724
17.9261
, http://www.100md.com
11.7178
3.0
27.3942
22.7212
18.5129
12.5247
2.5
27.7536
23.2358
18.9765
13.1332
2.0
, 百拇医药 28.0424
23.6373
18.3372
13.5139
1.5
28.2683
23.9389
19.6076
13.9311
1.0
28.4204
24.1491
, 百拇医药 19.7957
14.1634
表2为 u=250 mm(明视距离)处的物体发出的光线在各折射率面处发生折射后像的情况。 表2 明视距离物体经折射率均匀晶状体后的像(mm) h
角膜前面
角膜后面
晶状体前面
晶状体后面
4
28.3287
20.3569
16.3609
, 百拇医药
9.9772
3.5
29.0059
21.2827
17.2077
11.1612
3.0
29.5815
22.0298
17.8870
12.0352
2.5
, 百拇医药 30.0609
22.6304
18.4306
12.7030
2.0
30.4485
23.1042
18.8579
13.2130
1.5
30.7471
23.4630
, http://www.100md.com 19.1806
13.5910
1.0
30.9590
23.7146
19.4065
13.8525
由表1、表2可清楚看到,外来光线进入眼睛后,若晶状体的折射率均匀,则h=4 mm、1mm的光线在视网膜前成的像有较大的球差,影响术眼视力的提高。
(2)消除球差对晶状体折射率的要求
若只改变晶状体的折射率,其它各部位的光学参数都不变,以平行光线为例,消除球差需晶状体折射率分布如表3所示。 表3 消除平行光线球差对晶状体折射率的要求(mm) h
, 百拇医药
n
v
4
1.386
10.6095
3.5
1.409
10.5843
3.0
1.430
10.5862
2.5
1.448
, 百拇医药
10.6136
2.0
1.468
10.6423
1.5
1.477
10.6091
1.0
1.487
10.5939
根据表3得曲线如图6所示。图6显示,晶状体的折射率由边缘向中央呈线性增长,基本上能消除大量近轴光线在视网膜前的球差。

, 百拇医药
图6 消除平行光线球差对晶状体折射率的要求
4 讨论
(1)公式(4)中,当h
 r时,△→0;(3)式则转化为人们所熟知的近轴光线的单球面折射公式n1/u+n2/v=n2-n1/r说明(3)式是适用于非近轴光线和近轴光线的单球面折射成像的精确公式。
r时,△→0;(3)式则转化为人们所熟知的近轴光线的单球面折射公式n1/u+n2/v=n2-n1/r说明(3)式是适用于非近轴光线和近轴光线的单球面折射成像的精确公式。(2)为了简明问题解析过程,没有考虑晶状体改变曲率半径因素的影响。
(3)非近轴光线单球面折射成像公式可以解释晶状体消除球差的机理。其结果为人工晶状体制造提供了依据。
参考文献
[1] 刘普和,等.医学物理学[M].北京:人民卫生出版社,1988.
[2] V.B蒙卡斯尔.医学生理学[M].科学出版社,1988.
[3] 张承芬,徐国祥.激光眼科学[M].广东:广东科技出版社,1994.
收稿日期:1998-07-06, http://www.100md.com