日本血吸虫卵在BLAB/C鼠脾脏异位损害
作者：王 维 汪学龙
单位：安徽医科大学寄生虫学教研室， 安徽 合肥 230032
关键词：日本血吸虫卵；BALB/C鼠
疾病控制杂志990332 【文献标识码】 A
【中图分类号】 R195.1； O212
【文章编号】 1008-6013(1999)03-0224-02
Curve linearization and nonlinear regression
LOU Dong-hua
在医学研究的实际问题中，两个变量之间的回归关系大多是非线性的，这时选择恰当类型的曲线比拟合直线更符合实际情况。如：细菌培养中每一时刻的细菌总数y对时间x呈指数曲线，某病发病率y与时间x呈logistic曲线等。此时可以对因变量y和自变量x拟合一曲线，曲线拟合方法可分为两类：一类是传统的曲线直线化方法，是目前国内用的最多的一种方法，这种方法的显著特点是计算简便，模型参数检验有效；另一类方法是非线性回归法。
, 百拇医药
1 方法比较
1.1 曲线直线化 曲线直线化法，即利用变量变换的方法，使变换后的两个变量之间呈直线关系。求出直线回归方程后，再将方程中的变量通过逆变换还原，求得所求的曲线回归方程。例如某防治站重复治疗钩虫病人的次数x与复查阳性率(%)y呈指数曲线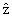
=eα+βx，作变换lny=z得
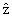=α+βx，利用最小二乘法使L=(z-).(z-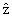)=min，求出α、β的最小二乘估计b=1xz/1xx,a=
-b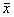
，得到关于z、x的直线回归方程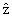=a+bx。再利用逆变换y=ez得到=ea+bx。
, 百拇医药
此法计算简便，但是最小二乘法最小值是变换后的z，换句话说，此时求出的最小二乘估计并不能保证使(y-).(y-)达到最小。
1.2 非线性回归 非线性回归模型y=F(β0，β1，…，βr，x1，…，xn)+ε=F(β)+ε通过极小化L(β)=(y-F(β)).(y-F(β)),求出β的估计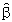
，但似然方程：
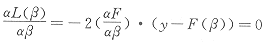没有显式解，所以采用选代法求解。
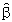, http://www.100md.com
2 实例分析
以文献中的某县1980～1996年月累计麻疹发病率(1/10万)的曲线拟合为例，原始数据1～12月累计(x)的发病率(y)依次为：0.279、0.920、2.078、4.393、8.144、12.174、17.306、18.435、18.728、18.965、19.230、19.328。图1是原始数据的散点图，散点呈“s”形，适宜拟合logistic曲线。
方法一：(曲线直线化)
作logistic变换z=ln〔K/(y-L)-1〕，其中L是下渐近线的坐标，K是上、下两渐近线的距离，从散点图中直观看出L最小值为0,K=19.36，对z、x作线性回归，求出回归方程z=4.913401-0.928010x再经变量转换得：=19.36/〔1+exp(4.913401-0.928010x)〕
, 百拇医药
=19.36/〔1+136.10151exp(-0.928010x)〕
各样本回归值与残差r如表1所示：
拟合优度R2=1-sse/sst=0.99680
图1 月累计麻疹发病率散点图
方法二：作非线性回归=19.36/(1+a.exp(bx))，用牛顿迭代法求出参数估计
a=200.00 b=-1.00即回归方程=19.36/(1+200.00exp(-1.00 x))，各样本回归值与残差r如表1。拟合优度R2=0.99736。
, 百拇医药
表1 两种方法的回归值与残差r 样 本
曲线直线化
非线性回归
x
y
r
r
1
0.279
, 百拇医药
0.35324
-0.07424
0.25960
0.01940
2
0.920
0.86926
0.05074
0.68978
0.23022
3
2.078
, 百拇医药 2.05748
0.02052
1.76684
0.31116
4
4.393
4.47667
-0.08367
4.15172
0.24128
5
8.144
8.36516
, http://www.100md.com
-0.22116
8.24676
-0.10276
6
12.174
12.74003
-0.56603
12.94334
-0.76934
7
17.306
16.06071
, 百拇医药
1.24529
16.37380
0.93550
8
18.435
17.90581
0.52919
18.14276
0.29224
9
18.728
18.75775
, http://www.100md.com
-0.02975
18.89367
-0.16567
10
18.965
19.11734
-0.15234
19.18579
-0.22079
11
19.230
19.26334
, 百拇医药
-0.03334
19.29555
-0.06555
12
19.328
19.32167
0.00633
19.33624
-0.00824
3 讨论
曲线直线化法和非线性回归都可以拟合曲线，但二者的出发点不一样，拟合的曲线方程也略有差异，拟合的效果从拟合优度R2来看，非线性回归优于曲线直线化。但是我们并不能保证非线性回归的参数估计的迭代能收敛，参数初始值的选取对迭代结果也有影响。实例中要拟合logistic曲线，首先得确定L和K的值，L与K的值在曲线直线化中只能凭直观得出，L与K值确定的好坏影响了最终的拟合效果，非线性回归可避免这一点，我们可以直接拟合曲线=L+K/〔1+a.exp(bx)〕将L、K也作为一待估参数，求出参数。
以上所有计算结果均是在统计软件SAS中编程得到。
【作者简介】 娄冬华(1967-)，男，讲师，理学硕士
(收稿日期 1999-04-16), 百拇医药
单位：安徽医科大学寄生虫学教研室， 安徽 合肥 230032
关键词：日本血吸虫卵；BALB/C鼠
疾病控制杂志990332 【文献标识码】 A
【中图分类号】 R195.1； O212
【文章编号】 1008-6013(1999)03-0224-02
Curve linearization and nonlinear regression
LOU Dong-hua
在医学研究的实际问题中，两个变量之间的回归关系大多是非线性的，这时选择恰当类型的曲线比拟合直线更符合实际情况。如：细菌培养中每一时刻的细菌总数y对时间x呈指数曲线，某病发病率y与时间x呈logistic曲线等。此时可以对因变量y和自变量x拟合一曲线，曲线拟合方法可分为两类：一类是传统的曲线直线化方法，是目前国内用的最多的一种方法，这种方法的显著特点是计算简便，模型参数检验有效；另一类方法是非线性回归法。
, 百拇医药
1 方法比较
1.1 曲线直线化 曲线直线化法，即利用变量变换的方法，使变换后的两个变量之间呈直线关系。求出直线回归方程后，再将方程中的变量通过逆变换还原，求得所求的曲线回归方程。例如某防治站重复治疗钩虫病人的次数x与复查阳性率(%)y呈指数曲线
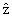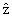=eα+βx，作变换lny=z得=α+βx，利用最小二乘法使L=(z-).(z-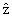)=min，求出α、β的最小二乘估计b=1xz/1xx,a=-b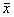，得到关于z、x的直线回归方程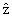=a+bx。再利用逆变换y=ez得到=ea+bx。, 百拇医药
此法计算简便，但是最小二乘法最小值是变换后的z，换句话说，此时求出的最小二乘估计并不能保证使(y-
).(y-)达到最小。1.2 非线性回归 非线性回归模型y=F(β0，β1，…，βr，x1，…，xn)+ε=F(β)+ε通过极小化L(β)=(y-F(β)).(y-F(β)),求出β的估计
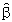，但似然方程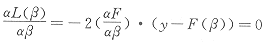：没有显式解，所以采用选代法求解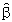。, http://www.100md.com
2 实例分析
以文献中的某县1980～1996年月累计麻疹发病率(1/10万)的曲线拟合为例，原始数据1～12月累计(x)的发病率(y)依次为：0.279、0.920、2.078、4.393、8.144、12.174、17.306、18.435、18.728、18.965、19.230、19.328。图1是原始数据的散点图，散点呈“s”形，适宜拟合logistic曲线。
方法一：(曲线直线化)
作logistic变换z=ln〔K/(y-L)-1〕，其中L是下渐近线的坐标，K是上、下两渐近线的距离，从散点图中直观看出L最小值为0,K=19.36，对z、x作线性回归，求出回归方程z=4.913401-0.928010x再经变量转换得：
=19.36/〔1+exp(4.913401-0.928010x)〕, 百拇医药
=19.36/〔1+136.10151exp(-0.928010x)〕
各样本回归值
与残差r如表1所示：拟合优度R2=1-sse/sst=0.99680
图1 月累计麻疹发病率散点图
方法二：作非线性回归
=19.36/(1+a.exp(bx))，用牛顿迭代法求出参数估计a=200.00 b=-1.00即回归方程
=19.36/(1+200.00exp(-1.00 x))，各样本回归值与残差r如表1。拟合优度R2=0.99736。, 百拇医药
表1 两种方法的回归值
与残差r 样 本曲线直线化
非线性回归
x
y
r
r
1
0.279
, 百拇医药
0.35324
-0.07424
0.25960
0.01940
2
0.920
0.86926
0.05074
0.68978
0.23022
3
2.078
, 百拇医药 2.05748
0.02052
1.76684
0.31116
4
4.393
4.47667
-0.08367
4.15172
0.24128
5
8.144
8.36516
, http://www.100md.com
-0.22116
8.24676
-0.10276
6
12.174
12.74003
-0.56603
12.94334
-0.76934
7
17.306
16.06071
, 百拇医药
1.24529
16.37380
0.93550
8
18.435
17.90581
0.52919
18.14276
0.29224
9
18.728
18.75775
, http://www.100md.com
-0.02975
18.89367
-0.16567
10
18.965
19.11734
-0.15234
19.18579
-0.22079
11
19.230
19.26334
, 百拇医药
-0.03334
19.29555
-0.06555
12
19.328
19.32167
0.00633
19.33624
-0.00824
3 讨论
曲线直线化法和非线性回归都可以拟合曲线，但二者的出发点不一样，拟合的曲线方程也略有差异，拟合的效果从拟合优度R2来看，非线性回归优于曲线直线化。但是我们并不能保证非线性回归的参数估计的迭代能收敛，参数初始值的选取对迭代结果也有影响。实例中要拟合logistic曲线，首先得确定L和K的值，L与K的值在曲线直线化中只能凭直观得出，L与K值确定的好坏影响了最终的拟合效果，非线性回归可避免这一点，我们可以直接拟合曲线
=L+K/〔1+a.exp(bx)〕将L、K也作为一待估参数，求出参数。以上所有计算结果均是在统计软件SAS中编程得到。
【作者简介】 娄冬华(1967-)，男，讲师，理学硕士
(收稿日期 1999-04-16), 百拇医药