用组内相关系数评价一致性的方法及其局限性
作者:蔡雪亚 金丕焕
单位:蔡雪亚 金丕焕 (200032 上海医科大学卫生统计与社会医学教研室)
关键词:
用组内相关系数评价一致性的方法及其局限性 在临床实际应用和调查中经常可以遇到某些观察值是由医生主观评定得出的(如量表评分等),不同医生对同一对象评定比较一致时,该指标比较理想,反之则较差,这就是指标即观察值的一致性(agreement)。一致性的测定是对相同的观察对象,或对不同的观察对象在进行多次测量后数值的接近程度。它所采用的方法因资料数据类型而有所不同[1]:
对于名义分类变量(categorical, nominal)采用的Kappa值及等级分类变量(categorical, ordinal)采用的加权Kappa值,国内很多文献上有报道及说明[2-4]。但对于计量资料,采用组内相关系数ICC[5](intraclass correlation coefficient)的并不多,举例说明。
, http://www.100md.com
为了鉴定某精神量表是否可行,请5位医生给3位病人用同一表在同一时间内评分(表1),究竟各位医生之间评分的一致性如何?
表1 医生评分表
患者序号
医生评分
1
2
3
4
5
1
24
25
, http://www.100md.com
23
25
23
2
8
9
9
8
7
3
10
15
18
17
, http://www.100md.com
15
虽然这是离散型的数据,但由于级别很多(评分为0~50分),不妨当作连续性资料来分析。在这里,要判断医生之间评分的差异性,就要用到组内相关系数ICC。ICC的计算是定义于相应方差(通常是对象之间的方差)相对于总体方差的比,主要用于连续性资料中观察一致性的测量,也可用于多等级资料[1]。
1.Fisher的ICC计算方法:早在1958年,Fisher[6]提出采用该方法来计算组内相关系数:假设共有m名被观察的对象,由2名观察者来评分,i取值1,2,……,m,那么
2. 用方差分析的方法计算ICC:上述方法也可用于观察者大于2的情况,但其组内相关系数ICC的计算却相当复杂,为此,Fisher又提出了下述计算公式: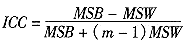
, http://www.100md.com
这就是利用方差分析的组内相关系数ICC计算。其中,m为处理组数(即被观察者的个数),MSB为组间均方(被观察者之间),MSW为组内均方(观察者之间)。用上面的例子计算可得: MSB=314.865 ,MSW=1.6 ,ICC=0.984 9。
结论:医生之间评分的一致性很好。
3. 有缺失值时ICC值的计算方法:Smith的ICC计算方法中,加入了医生评定次数的权重。它的计算方法虽然也是利用方差分析来计算组内相关系数,但是,由于考虑到了每位对象(病人)被观察的次数,其ICC值更为精确。设第i层加权系数υi,它是由每位病人被观察的次数来决定的,N为总的观察次数。定义V=Σivi,Vc=Σi(1-vi/V),V0=(V-Σiv2i/V)/Vc,a=Vc(N-m),b=Vc.V0-1/(N-m),就得到了Smith 的估计值。SXv=Σivi(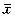 i-
i-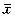 v)2,SEa=ΣaSSi,SEb=ΣbSSi,ICC=(SXv-SEa)/(SXv+SEb)仍以该例说明这种计算方法(表2),但其中部分为缺失值。
v)2,SEa=ΣaSSi,SEb=ΣbSSi,ICC=(SXv-SEa)/(SXv+SEb)仍以该例说明这种计算方法(表2),但其中部分为缺失值。
, 百拇医药
表2 有缺失值时医生评分表
患者
序号
医生评分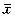
υi
SSi
1
2
3
4
, 百拇医药
5
1
24
25…
25
23
24.25
4
2.75
2
8…
9
8
7
, 百拇医药
8.00
4
2.00
3
14
16
14
15
15
14.80
5
2.80
合计
, http://www.100md.com 15.62
7.55
V=13, Vc=(1-4/13)+(1-4/13)+(1-5/13)=2,V0=[13-(42/13+42/13+52/13)]/2=4.31,a=2/(13-3)=0.2,b=2×(4.31-1)/(13-3)=0.67。ICC值计算:SXv=4×(24.25-15.62)2+4×(8-15.62)2+5×(14.8-15.62)2=533.53,SEa=0.17×7.55=1.28,SEb=0.67×7.55=4.98,ICC=0.988 4。
结论:各位医生评分的一致性很好。
, 百拇医药
在我们的实践中发现,如果不同病人的评分差别较大,即病人病情严重程度差别较大时,ICC容易得出较为准确的值。如果病人之间的评分很接近,即病人的病情基本相似时,ICC的计算值就与事实不符了。比如在上面的例2中,如果3个病人的得分基本一致的话,得出的ICC值就很低。我们将上述资料做一些适当修改(表3)。
表3 适当修改后医生评分表
患者
序号
医生评分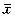
ΣX
ΣX2
, http://www.100md.com
SSi
1
2
3
4
5
1
9
8
8
9
8
8.4
42
, 百拇医药
354
1.2
2
7
8
9
8
8
8.0
40
322
2.0
3
8
, 百拇医药
9
8
9
7
8.2
41
339
2.8
合计
8.2
123
1 015
6.0
再次计算ICC值。Fisher法:MSB=0.2, MSW=1,ICC=-0.36 。Smith法:υi =5, a=0.17, b= 0.67, SXv=0.4, SEa=1.02, SEb=4.02,ICC=-0.140。
, http://www.100md.com
看出,医生评分的一致性很好,但计算的ICC值却非常低,并且出现了负值。所以,对于病人状况较接近,组内相关系数ICC就不能正确地反映医生评分的一致性了。
参考文献
1 Armitage P , Colton T. Encyclopedia of biostatistics . England: John Wiley & Sons Ltd, 1998.1502-1503.
2 赵跃进. 一致性检验方法及应用. 中华预防医学杂志, 1991, 25: 238-240.
3 黄正南. 一致系数的公式及其与相关系数的关系. 中国卫生统计, 1995, 12:1-3.
4 文万青. 重复性和真实性的评价方法. 中华预防医学杂志,1995,29:235-237.
5 颜文伟. 检验一致性的统计方法. 中华神经精神科杂志,1986,19:367-371.
6 Fisher RA. Statistical methods for research workers. 13th ed . Britain: Oliver and Biyd Ltd, 1958. 211-215.
收稿日期:1998-05-29 修回日期:1998-12-23, http://www.100md.com
单位:蔡雪亚 金丕焕 (200032 上海医科大学卫生统计与社会医学教研室)
关键词:
用组内相关系数评价一致性的方法及其局限性 在临床实际应用和调查中经常可以遇到某些观察值是由医生主观评定得出的(如量表评分等),不同医生对同一对象评定比较一致时,该指标比较理想,反之则较差,这就是指标即观察值的一致性(agreement)。一致性的测定是对相同的观察对象,或对不同的观察对象在进行多次测量后数值的接近程度。它所采用的方法因资料数据类型而有所不同[1]:
对于名义分类变量(categorical, nominal)采用的Kappa值及等级分类变量(categorical, ordinal)采用的加权Kappa值,国内很多文献上有报道及说明[2-4]。但对于计量资料,采用组内相关系数ICC[5](intraclass correlation coefficient)的并不多,举例说明。
, http://www.100md.com
为了鉴定某精神量表是否可行,请5位医生给3位病人用同一表在同一时间内评分(表1),究竟各位医生之间评分的一致性如何?
表1 医生评分表
患者序号
医生评分
1
2
3
4
5
1
24
25
, http://www.100md.com
23
25
23
2
8
9
9
8
7
3
10
15
18
17
, http://www.100md.com
15
虽然这是离散型的数据,但由于级别很多(评分为0~50分),不妨当作连续性资料来分析。在这里,要判断医生之间评分的差异性,就要用到组内相关系数ICC。ICC的计算是定义于相应方差(通常是对象之间的方差)相对于总体方差的比,主要用于连续性资料中观察一致性的测量,也可用于多等级资料[1]。
1.Fisher的ICC计算方法:早在1958年,Fisher[6]提出采用该方法来计算组内相关系数:假设共有m名被观察的对象,由2名观察者来评分,i取值1,2,……,m,那么

2. 用方差分析的方法计算ICC:上述方法也可用于观察者大于2的情况,但其组内相关系数ICC的计算却相当复杂,为此,Fisher又提出了下述计算公式:
, http://www.100md.com
这就是利用方差分析的组内相关系数ICC计算。其中,m为处理组数(即被观察者的个数),MSB为组间均方(被观察者之间),MSW为组内均方(观察者之间)。用上面的例子计算可得: MSB=314.865 ,MSW=1.6 ,ICC=0.984 9。
结论:医生之间评分的一致性很好。
3. 有缺失值时ICC值的计算方法:Smith的ICC计算方法中,加入了医生评定次数的权重。它的计算方法虽然也是利用方差分析来计算组内相关系数,但是,由于考虑到了每位对象(病人)被观察的次数,其ICC值更为精确。设第i层加权系数υi,它是由每位病人被观察的次数来决定的,N为总的观察次数。定义V=Σivi,Vc=Σi(1-vi/V),V0=(V-Σiv2i/V)/Vc,a=Vc(N-m),b=Vc.V0-1/(N-m),就得到了Smith 的估计值。SXv=Σivi(
, 百拇医药
表2 有缺失值时医生评分表
患者
序号
医生评分
υi
SSi
1
2
3
4
, 百拇医药
5
1
24
25…
25
23
24.25
4
2.75
2
8…
9
8
7
, 百拇医药
8.00
4
2.00
3
14
16
14
15
15
14.80
5
2.80
合计
, http://www.100md.com 15.62
7.55
V=13, Vc=(1-4/13)+(1-4/13)+(1-5/13)=2,V0=[13-(42/13+42/13+52/13)]/2=4.31,a=2/(13-3)=0.2,b=2×(4.31-1)/(13-3)=0.67。ICC值计算:SXv=4×(24.25-15.62)2+4×(8-15.62)2+5×(14.8-15.62)2=533.53,SEa=0.17×7.55=1.28,SEb=0.67×7.55=4.98,ICC=0.988 4。
结论:各位医生评分的一致性很好。
, 百拇医药
在我们的实践中发现,如果不同病人的评分差别较大,即病人病情严重程度差别较大时,ICC容易得出较为准确的值。如果病人之间的评分很接近,即病人的病情基本相似时,ICC的计算值就与事实不符了。比如在上面的例2中,如果3个病人的得分基本一致的话,得出的ICC值就很低。我们将上述资料做一些适当修改(表3)。
表3 适当修改后医生评分表
患者
序号
医生评分
ΣX
ΣX2
, http://www.100md.com
SSi
1
2
3
4
5
1
9
8
8
9
8
8.4
42
, 百拇医药
354
1.2
2
7
8
9
8
8
8.0
40
322
2.0
3
8
, 百拇医药
9
8
9
7
8.2
41
339
2.8
合计
8.2
123
1 015
6.0
再次计算ICC值。Fisher法:MSB=0.2, MSW=1,ICC=-0.36 。Smith法:υi =5, a=0.17, b= 0.67, SXv=0.4, SEa=1.02, SEb=4.02,ICC=-0.140。
, http://www.100md.com
看出,医生评分的一致性很好,但计算的ICC值却非常低,并且出现了负值。所以,对于病人状况较接近,组内相关系数ICC就不能正确地反映医生评分的一致性了。
参考文献
1 Armitage P , Colton T. Encyclopedia of biostatistics . England: John Wiley & Sons Ltd, 1998.1502-1503.
2 赵跃进. 一致性检验方法及应用. 中华预防医学杂志, 1991, 25: 238-240.
3 黄正南. 一致系数的公式及其与相关系数的关系. 中国卫生统计, 1995, 12:1-3.
4 文万青. 重复性和真实性的评价方法. 中华预防医学杂志,1995,29:235-237.
5 颜文伟. 检验一致性的统计方法. 中华神经精神科杂志,1986,19:367-371.
6 Fisher RA. Statistical methods for research workers. 13th ed . Britain: Oliver and Biyd Ltd, 1958. 211-215.
收稿日期:1998-05-29 修回日期:1998-12-23, http://www.100md.com