Bootstrap方法在评价Cox模型预测能力方面的应用
作者：刘勤 金丕焕 高尔生
单位：刘勤 金丕焕 高尔生 (200032 上海医科大学卫生统计教研室)
关键词：
中华预防医学杂志990317 在多因素生存分析研究中，常用Cox模型来发现预后因素，并对新病人的预后进行预测，预测能力好的模型才能使医务人员对新病例的预后进行准确的估计，进而采取恰当的防治策略。
现在常用的评价指标是一致性指数c[1]，它估计了预测结果与实际观察到的结果相一致的概率。虽然c的应用广泛，也易于解释，但是在比较两个模型的预测准确度时，它对两个模型的较小差异不敏感。为了避免这些不足，我们用Bootstrap方法来评价所拟合的Cox模型对各时点生存率估计的准确程度,从而判断模型的预测能力。
一、原理和方法
, 百拇医药
1.原理：如果所建立的Cox模型对源于同一总体但是不属于训练样本的新样本的生存率的预测与实际情况相符合，说明这一模型预测效果较好。一般把Cox模型预测的生存率与Kaplan-Meier的PL法生存率作比较,两者间差距越小越好。但是,我们所能看到的两者间的差值不是真正的Cox模型预测的总体生存率与实际生存率的差值，而仅仅是用样本估计出的表面上的差值(简记为Dapp)。由于抽样误差的存在，这个表面差值与真实差值(简记为D)之间还可能存在差距(简记为DD)。如果DD=0，则可以直接用Dapp作为D的点估计；如果DD≠0，则D=Dapp-DD。显而易见，D越小，两种生存率一致性越好。可见，考察一个Cox模型对总体生存率进行预测时的偏差大小，关键是要估计出DD的平均大小，本研究用Bootstrap方法来解决上述的估计问题[2-4]。
2.Bootstrap方法评价Cox模型生存率预测能力的步骤：
, http://www.100md.com
(1)令：Sc(t)=用原始样本拟合的Cox模型估计原始样本在时点t的平均生存率， Spl(t) =用Kaplan-Meier的乘积极限法估计的原始样本在时点t的生存率，Dapp=Sc(t)-Spl(t) ；S*c(t)=用自助样本拟合的Cox模型估计的自助样本本身在时点t的平均生存率，S*pl(t)=用Kaplan-Meier的乘积极限法估计自助样本时点t的生存率，D*app(t)=S*c(t)-S*pl(t) ；S*oc(t)=用自助样本拟合的Cox模型估计的原始样本在时点t的平均生存率，D*o(t)=S*oc(t)-Spl(t)，DD(t)=D*app(t)-D*o(t)。
, 百拇医药
(2)确定备选因素、因素选取方式(逐步回归、前进法、后退法、最优子集法等，根据需要选择其一)及因素选取水准α。
(3)用原始样本按照第2步拟合Cox模型，计算Sc(t)、Spl(t)及Dapp(t)。
(4)从原始样本中产生一个自助样本，把第3步得到的Cox模型中的因素作为预后因素(自变量)对自助样本拟合Cox模型，计算S*c(t)、S*pl(t)及D*app(t)。
(5)用第4步自助样本拟合的Cox模型去估计原始样本的生存率，其估计值为S*oc(t)，计算它与原始样本的PL生存率的差值D*o(t)。
, 百拇医药
(6)计算DD(t)。
(7)重复4～6步100次(Efron认为，自助样本一般取50～100个可以得到统计量标准误的较好估计)。
(8)由于每一个自助样本在时点t不一定都有死亡发生，因此完成第7步后得到的DD(t)的个数可能小于或等于100个，以M表示之，计算DD(t)的均值，即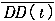
=DD(t)/M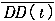，[是通过自助样本估计的源于总体的随机样本拟合的Cox模型预测的生存率与实际生存率的表面偏差与实际偏差的平均差距]。
(9)用D(t)=Dapp(t)-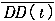来估计实际偏差。
, 百拇医药
(10)计算原始样本PL生存率的95%可信区间，如果Sc(t)在Spl(t)的95%可信区间内，可以认为所拟合的Cox模型在时点t的预测结果具有一定的可信性，在此基础上D(t)的绝对值越小，模型的预测准确度越高。
(11)考察Cox模型对多个生存时点的预测效果，如果都得到较好的结果，说明所拟合的模型较优，预测结果可靠。
二、实例应用
WHO课题(91236)“健康教育对哺乳和避孕行为的影响——上海市产后哺乳和避孕行为的队列研究”的目的之一是探索健康教育能否使产后第1年的意外妊娠率显著下降。研究对象为怀孕满34周左右、即将分娩、在指定的6家妇保院(所)接受产前检查及保健服务的已婚妇女。研究对象被随机分入试验组和对照组。进入试验组的妇女及其丈夫接受一部附加的有关产后哺乳和避孕的健康教育录像节目，对照组妇女仅接受常规的保健服务。观察这些妇女产后1年意外妊娠发生的情况，分析影响产后意外妊娠发生率的因素。产后观察时间小于或等于1年的研究对象有756人，其中教育组372人，对照组384人，在产后1年内发生意外妊娠的总人数为294人。
, 百拇医药
设Cox模型因素选取水准α=0.05。以1年内发生意外妊娠作为事件发生，以组别(x1)、以前是否接受过有关的宣传教育(x2)、夫、妻文化水平(x3、x4) 、夫是否农村户口(x5)、夫是否城市户口(x6)、妻是否农村户口(x7)、妻是否城市户口(x8)等因素作为备选因素拟合Cox模型。
用Bootstrap方法筛选出的预后因素是x1(组别)和x2(进入研究前是否接受过有关卫生宣教)；对原始样本逐步回归拟合的Cox模型包括x1、x2和x6(丈夫是否城市户口)；如果考虑x6和x8(妻子是否城市户口)高度相关，认为如果x6是预后因素，那么x8也应该是预后因素，由此可以构造如下3种Cox模型。
, 百拇医药
以x1和x2为预后因素，拟合的Cox模型生存函数是：
S(t,x)=[S0(t)]exp(-0.212 2x1-0.373 1x2) (1)
逐步回归Cox模型生存函数是：
S(t,x)=[S0(t)]exp(-0.287 05x1-0.422 4x2+0.418 8x6) (2)
用x1、x2、x6和x8作为预后因素拟合的Cox模型生存函数如下：
, 百拇医药
S(t,x)=[S0(t)]exp(-0.288 8x1-0.428 1x2+0.268 1x6+0.169 8x8) (3)
以上3个模型经似然比检验都具有统计学意义。但是其中哪一个模型的预测能力最好，我们按照上述步骤进行计算，结果见表1。
表1 各Cox模型预测的生存率与PL生存率的
实际偏差[D(t)]估计 时点(天)
D(t)模型(1)
D(t)模型(2)
, 百拇医药
D(t)模型(3)
0
30
-0.000 256 8
-0.000 171 9
-0.000 245 9
60
0.000 243 8
0.000 512 6
0.000 305 6
90
0.001 070 0
, http://www.100md.com
0.001 529 2
0.001 212 1
120
150
180
0.000 850 0
0.002 760 0
0.000 895 9
210
0.001 784 8
0.004 047 2
0.001 547 4
, 百拇医药
240
0.001 424 4
0.004 260 2
0.002 825 6
270
0.005 983 2
0.009 471 2
0.005 977 9
300
330
360
0.000 666 8
, 百拇医药
0.003 014 4
-0.004 194 9
从表1可见，除了t=30天，D(t)模型(2)最小，t=210和270天D(t)模型(3)略小于D(t)模型(1)外，其余时点各模型的实际偏差D(t)从小到大排列的次序是：模型(1)<模型(3)<模型(2)，说明模型(1)的预测准确度总的来说高于其他两种模型，用于预测效果最好，也说明模型(1)拟合较优。
3个模型都反映出“试验组”和“进入研究前接受过有关卫生宣教”对降低产后1年内意外妊娠率有促进作用，从实际意义来讲，这是合情合理的；而模型(2)和模型(3)还分别提示“丈夫是城市户口”和“妻子是城市户口”是增加产后1年内意外妊娠率的危险因素，这点从实际意义上看有一定的可能性，比如有人认为城市夫妻文化程度高的居多，在产后避孕方面容易自作主张，导致避孕失败，但是这种解释有些牵强，本资料不能提供充分的证据。因此，从实际意义来看，也是模型(1)较可靠。
, 百拇医药
三、讨论
在实际应用中，预测是建立模型的一个重要目的。因此，对模型预测能力的评价非常重要。Bootstrap方法评价Cox模型的预测能力，不仅可以估计模型在各时点的预测准确度，计算校正的点估计，而且可以综合各时点的预测情况评价模型总的预测能力。本研究估计了Cox模型生存率与实际生存率的表面差值与实际差值的偏差，从而避免了过度估计。据此还可以评价模型拟合的优劣。
参考文献
1 Harrell FE Jr,Califf RM,Pryor DB,et al, Evaluating the yield of medical tests. JAMA, 1982,247:2543-2546.
2 Efron B, Gong G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am Stat, 1983,37:36-48.
3 Altman DG ,Andersen PK. Bootstrap investigation of the stability of a Cox regression model. Stat Med, 1989,8:771-783.
4 刘勤，金丕焕. Bootstrap方法及其在医学统计中的应用. 中华预防医学杂志，1998，32：52-53.
收稿日期：1998-07-02 修回日期：1998-08-04, 百拇医药
单位：刘勤 金丕焕 高尔生 (200032 上海医科大学卫生统计教研室)
关键词：
中华预防医学杂志990317 在多因素生存分析研究中，常用Cox模型来发现预后因素，并对新病人的预后进行预测，预测能力好的模型才能使医务人员对新病例的预后进行准确的估计，进而采取恰当的防治策略。
现在常用的评价指标是一致性指数c[1]，它估计了预测结果与实际观察到的结果相一致的概率。虽然c的应用广泛，也易于解释，但是在比较两个模型的预测准确度时，它对两个模型的较小差异不敏感。为了避免这些不足，我们用Bootstrap方法来评价所拟合的Cox模型对各时点生存率估计的准确程度,从而判断模型的预测能力。
一、原理和方法
, 百拇医药
1.原理：如果所建立的Cox模型对源于同一总体但是不属于训练样本的新样本的生存率的预测与实际情况相符合，说明这一模型预测效果较好。一般把Cox模型预测的生存率与Kaplan-Meier的PL法生存率作比较,两者间差距越小越好。但是,我们所能看到的两者间的差值不是真正的Cox模型预测的总体生存率与实际生存率的差值，而仅仅是用样本估计出的表面上的差值(简记为Dapp)。由于抽样误差的存在，这个表面差值与真实差值(简记为D)之间还可能存在差距(简记为DD)。如果DD=0，则可以直接用Dapp作为D的点估计；如果DD≠0，则D=Dapp-DD。显而易见，D越小，两种生存率一致性越好。可见，考察一个Cox模型对总体生存率进行预测时的偏差大小，关键是要估计出DD的平均大小，本研究用Bootstrap方法来解决上述的估计问题[2-4]。
2.Bootstrap方法评价Cox模型生存率预测能力的步骤：
, http://www.100md.com
(1)令：Sc(t)=用原始样本拟合的Cox模型估计原始样本在时点t的平均生存率， Spl(t) =用Kaplan-Meier的乘积极限法估计的原始样本在时点t的生存率，Dapp=Sc(t)-Spl(t) ；S*c(t)=用自助样本拟合的Cox模型估计的自助样本本身在时点t的平均生存率，S*pl(t)=用Kaplan-Meier的乘积极限法估计自助样本时点t的生存率，D*app(t)=S*c(t)-S*pl(t) ；S*oc(t)=用自助样本拟合的Cox模型估计的原始样本在时点t的平均生存率，D*o(t)=S*oc(t)-Spl(t)，DD(t)=D*app(t)-D*o(t)。
, 百拇医药
(2)确定备选因素、因素选取方式(逐步回归、前进法、后退法、最优子集法等，根据需要选择其一)及因素选取水准α。
(3)用原始样本按照第2步拟合Cox模型，计算Sc(t)、Spl(t)及Dapp(t)。
(4)从原始样本中产生一个自助样本，把第3步得到的Cox模型中的因素作为预后因素(自变量)对自助样本拟合Cox模型，计算S*c(t)、S*pl(t)及D*app(t)。
(5)用第4步自助样本拟合的Cox模型去估计原始样本的生存率，其估计值为S*oc(t)，计算它与原始样本的PL生存率的差值D*o(t)。
, 百拇医药
(6)计算DD(t)。
(7)重复4～6步100次(Efron认为，自助样本一般取50～100个可以得到统计量标准误的较好估计)。
(8)由于每一个自助样本在时点t不一定都有死亡发生，因此完成第7步后得到的DD(t)的个数可能小于或等于100个，以M表示之，计算DD(t)的均值，即
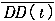=DD(t)/M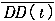，[是通过自助样本估计的源于总体的随机样本拟合的Cox模型预测的生存率与实际生存率的表面偏差与实际偏差的平均差距]。(9)用D(t)=Dapp(t)-
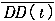来估计实际偏差。, 百拇医药
(10)计算原始样本PL生存率的95%可信区间，如果Sc(t)在Spl(t)的95%可信区间内，可以认为所拟合的Cox模型在时点t的预测结果具有一定的可信性，在此基础上D(t)的绝对值越小，模型的预测准确度越高。
(11)考察Cox模型对多个生存时点的预测效果，如果都得到较好的结果，说明所拟合的模型较优，预测结果可靠。
二、实例应用
WHO课题(91236)“健康教育对哺乳和避孕行为的影响——上海市产后哺乳和避孕行为的队列研究”的目的之一是探索健康教育能否使产后第1年的意外妊娠率显著下降。研究对象为怀孕满34周左右、即将分娩、在指定的6家妇保院(所)接受产前检查及保健服务的已婚妇女。研究对象被随机分入试验组和对照组。进入试验组的妇女及其丈夫接受一部附加的有关产后哺乳和避孕的健康教育录像节目，对照组妇女仅接受常规的保健服务。观察这些妇女产后1年意外妊娠发生的情况，分析影响产后意外妊娠发生率的因素。产后观察时间小于或等于1年的研究对象有756人，其中教育组372人，对照组384人，在产后1年内发生意外妊娠的总人数为294人。
, 百拇医药
设Cox模型因素选取水准α=0.05。以1年内发生意外妊娠作为事件发生，以组别(x1)、以前是否接受过有关的宣传教育(x2)、夫、妻文化水平(x3、x4) 、夫是否农村户口(x5)、夫是否城市户口(x6)、妻是否农村户口(x7)、妻是否城市户口(x8)等因素作为备选因素拟合Cox模型。
用Bootstrap方法筛选出的预后因素是x1(组别)和x2(进入研究前是否接受过有关卫生宣教)；对原始样本逐步回归拟合的Cox模型包括x1、x2和x6(丈夫是否城市户口)；如果考虑x6和x8(妻子是否城市户口)高度相关，认为如果x6是预后因素，那么x8也应该是预后因素，由此可以构造如下3种Cox模型。
, 百拇医药
以x1和x2为预后因素，拟合的Cox模型生存函数是：
S(t,x)=[S0(t)]exp(-0.212 2x1-0.373 1x2) (1)
逐步回归Cox模型生存函数是：
S(t,x)=[S0(t)]exp(-0.287 05x1-0.422 4x2+0.418 8x6) (2)
用x1、x2、x6和x8作为预后因素拟合的Cox模型生存函数如下：
, 百拇医药
S(t,x)=[S0(t)]exp(-0.288 8x1-0.428 1x2+0.268 1x6+0.169 8x8) (3)
以上3个模型经似然比检验都具有统计学意义。但是其中哪一个模型的预测能力最好，我们按照上述步骤进行计算，结果见表1。
表1 各Cox模型预测的生存率与PL生存率的
实际偏差[D(t)]估计 时点(天)
D(t)模型(1)
D(t)模型(2)
, 百拇医药
D(t)模型(3)
0
30
-0.000 256 8
-0.000 171 9
-0.000 245 9
60
0.000 243 8
0.000 512 6
0.000 305 6
90
0.001 070 0
, http://www.100md.com
0.001 529 2
0.001 212 1
120
150
180
0.000 850 0
0.002 760 0
0.000 895 9
210
0.001 784 8
0.004 047 2
0.001 547 4
, 百拇医药
240
0.001 424 4
0.004 260 2
0.002 825 6
270
0.005 983 2
0.009 471 2
0.005 977 9
300
330
360
0.000 666 8
, 百拇医药
0.003 014 4
-0.004 194 9
从表1可见，除了t=30天，D(t)模型(2)最小，t=210和270天D(t)模型(3)略小于D(t)模型(1)外，其余时点各模型的实际偏差D(t)从小到大排列的次序是：模型(1)<模型(3)<模型(2)，说明模型(1)的预测准确度总的来说高于其他两种模型，用于预测效果最好，也说明模型(1)拟合较优。
3个模型都反映出“试验组”和“进入研究前接受过有关卫生宣教”对降低产后1年内意外妊娠率有促进作用，从实际意义来讲，这是合情合理的；而模型(2)和模型(3)还分别提示“丈夫是城市户口”和“妻子是城市户口”是增加产后1年内意外妊娠率的危险因素，这点从实际意义上看有一定的可能性，比如有人认为城市夫妻文化程度高的居多，在产后避孕方面容易自作主张，导致避孕失败，但是这种解释有些牵强，本资料不能提供充分的证据。因此，从实际意义来看，也是模型(1)较可靠。
, 百拇医药
三、讨论
在实际应用中，预测是建立模型的一个重要目的。因此，对模型预测能力的评价非常重要。Bootstrap方法评价Cox模型的预测能力，不仅可以估计模型在各时点的预测准确度，计算校正的点估计，而且可以综合各时点的预测情况评价模型总的预测能力。本研究估计了Cox模型生存率与实际生存率的表面差值与实际差值的偏差，从而避免了过度估计。据此还可以评价模型拟合的优劣。
参考文献
1 Harrell FE Jr,Califf RM,Pryor DB,et al, Evaluating the yield of medical tests. JAMA, 1982,247:2543-2546.
2 Efron B, Gong G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am Stat, 1983,37:36-48.
3 Altman DG ,Andersen PK. Bootstrap investigation of the stability of a Cox regression model. Stat Med, 1989,8:771-783.
4 刘勤，金丕焕. Bootstrap方法及其在医学统计中的应用. 中华预防医学杂志，1998，32：52-53.
收稿日期：1998-07-02 修回日期：1998-08-04, 百拇医药