利用小波级数检测癫痫EEG中的棘波*
作者:宦飞 郑崇勋 黄远桂
单位:宦飞 郑崇勋 西安交通大学生物医学工程研究所,西安 710049;黄远桂 第四军医大学西京医院,西安 710032)
关键词:小波级数;脑电图;癫痫;自动检测
航天医学与医学工程/990312摘要: 目的 研究自动提取癫痫脑电中棘波。 方法 把EEG信号分解成小波级数,在各个尺度上,利用信号细节在两个过零点之间的平均振幅确定瞬态波形的大小,通过选择平均振幅中的局部极值检测棘波。 结果 对6位患者的EEG信号进行处理,检测棘波的正确率为79.66%。 结论 这种方法能够比较准确地检测EEG中的棘波。
中图分类号: R318.03 文献标识码:A 文章编号:1002-0837(1999)03-0200-04
Detection of Spikes in Epileptic EEG by Using Wavelet Series.
, 百拇医药
HUAN Fei
Biomedical Engineering Institute, Xi'an
Jiaotong University, Xi'an 710049,China
ZHENG Chong-xun,HUANG Yuan-Gui.Space
Medicine & Medical Engineering,1999,12(3):200~203
Abstract: Objective To study automatic detection of the spikes in the epileptic EEG signals. Method Based on wavelet series decomposition of EEG signals, the mean amplitude between two cross-zeros of the detail signals at every scale was utilized to obtain quantitative values for the transient waves, and the abnormal spikes were distinguished from normal background EEG activities by the local maximum of the mean amplitudes of the different scales. Result The analysis of 6 patients' EEG data showed that the correctness ratio was 79.66% in detecting the spikes. Conclusion The epileptiform spikes in the abnormal EEG can be accurately detected with this method.
, 百拇医药
Key words: wavelet series;EEG;epilepsy;automatic detection
脑电图(EEG)中的瞬态特征往往具有重要的诊断意义,检测EEG信号中的瞬态特征波形对于诊断癫痫尤为重要。临床上有典型癫痫发作的患者,大部分可以在EEG检查中发现癫痫样特征波形(癫痫波)。癫痫波主要有以下几种:棘波(或尖波)、棘(或尖)慢复合波、以及多棘波群等。因此,癫痫脑电的检测,主要是EEG信号中棘波的检测。从60年代起,棘波的自动检测技术就受到了注意,许多学者在这一领域做了大量的研究,提出了多种方法[1~6]。然而,到目前为止,这一领域仍然没有取得重大进展。近年来,小波变换技术已在生物信号的处理领域得到广泛的应用[7,8]。本文利用小波变换方法的特点,设计了一个使用小波级数检测EEG中癫痫样棘波的方法。
数据采集
EEG数据采自在西京医院神经内科脑电图和脑地形图室作临床检查的患者。使用的脑电放大器是Chocolate 8816型,滤波器的通带为0.15~60 Hz,A/D转换器12位,采样率为200 Hz。使用头皮电极记录脑电,电极安放采用国际标准10-20连接方式,以双耳作为参考电极,前额为地电极,同时记录16导脑电数据。在检验过程中,采用睁眼闭眼、过度换气和美解眠药物注射三种方式诱发癫痫性放电。
, http://www.100md.com
小波级数的计算
信号x[n],n=0,1,…N,在尺度j=1,2,…,J(J≤M)上的小波级数为: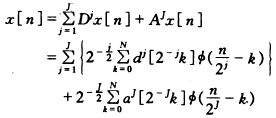 (1)
(1)
其中,Djx[n]和Ajx[n]分别是信号x[n]在尺度j上的逼近和细节。本文使用三次B-样条生成的正交小波基[9]计算EEG信号的小波级数。
棘波检测
下面,分析如何利用小波级数检测EEG中的棘波。一段长度N=1024个样点(5.12s)的EEG信号s中含有两个棘波,分别记为SA和SB,如图1(a)所示。把s分解成4个尺度j=1,2,3,4上的小波级数,在尺度j=1,2,3,4上s的细节分别记为D1、D2、D3和D4,如图1(b)、(c)、(d)和(e)所示。图1(f)是s在尺度上的逼近A4。从图1(b)、(c)、(d)和(e)中可以看出,对应信号s中棘波SA和SB出现的时刻,在细节D1、D2、D3和D4中呈现高幅振荡,在尺度j=2,3,4上尤为明显,见图1(c)、(d)和(e)。
, 百拇医药
图1 (a)原始EEG信号s,(b)~(e)s的细节D1、D2、D3和D4,(f)s的逼近A4
Fig.1 (a) EEG signal s, (b)~(e) detailed D1, D2, D3, and D4 of s, (f) approximation A4 of s
在任一个尺度上,我们使用两个过零点之间的平均振幅,相当于半个周期里的平均振幅,度量信号细节的震荡大小。这样做的好处是,当某个时间间隔里,细节中含有多个高幅震荡时,平均振幅只有一个极值,并且,这个极值对应震荡最大的半个周期,而震荡最大的半周期恰好就是原始EEG信号中棘波峰值所在的时间间隔。
对图1(a)中的s,分别计算尺度j=1,2,3,4上细节的半周期平均振幅,并且记为MD1、MD2、MD3和MD4,见图2(b)~(e)。从图2(c)、(d)和(e)可以看出,对应SA和SB出现的时刻,在MD2、MD3和MD4中出现比较显著的局部极大值。这样,可以根据某一时刻、某些尺度上细节的半周期平均振幅的局部极大值,利用某种算法检测EEG信号中的棘波。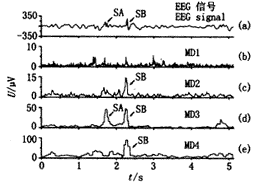
, 百拇医药
图2 (a)原始EEG信号s,(b)~(e)s在尺度j=1,2,3,4上的细节的半周期平均振幅MD1、MD2、MD3和MD4
Fig.2 (a) EEG signal s, (b)~(e) the mean values between two cross-zeros MD1, MD2, MD3, and MD4 of the details at the scales j=1,2,3,4 of s
下面给出具体的检测方法。
(1)计算局部极值
假设{aj0,aj1,…ajN-1}是尺度j上信号细节的半周期平均振幅序列,对于任一个点n,{ajn-l,…,ajn-1,ajn,ajn+l}是以n为中心,长度为2l+1的一个子序列,利用不等式,Ajn=ajn,如果ajn=max{ajn-l,…,ajn-1,ajn,ajn+l} (2a)
, http://www.100md.com
Ajn=0,如果ajn≠max{ajn-l,…,ajn-1,ajn,ajn+l} (2b)
产生一个新序列Ajn(0≤n≤N-1,显然Ajn≠0,如果,则在n点出现局部极值。这里,取l=2j-1/2*8当采样率为200 Hz时,8个样点相当于40 ms)。
(2)计算Ajn中所有不相同的极值{bj0,bj1,…bjM}的均值mbj。
, http://www.100md.com
(3)选择与棘波相关的局部极值
a.如果Ajn>=mbj,Bjn=Ajn,否则Bjn=0。得到Bj0,Bj1,…BjN-1;
b. 在尺度j=1,2,3,4上,给定适当的阀值θj,j=1,2,3,4。如果Bjn≥θj,,则Sjn=Bjn;当时Bjn<θj,如果在至少两个其它尺度上,在区间[n-l,n+l]内包含不为零的Bjn(i≠j),则取Sjn=Bjn;否则取Sjn=0;
, http://www.100md.com
c.如果Sjn>0,原始EEG信号在区间[n-l,n+l]内的幅值的绝对值的最大值的小于某个阀值ε,则取Sjn=0。
经过上述步骤后,以尺度j=2,3,4上的序列{Sjn}作为与棘波相关的局部极值,根据这些局部极值检测EEG信号中的棘波。图3给出了利用小波级数检测信号中sn棘波的结果。检测选用的参数为:θ1=6.25,θ2=12.5,θ3=25.0,θ4=50.0,ε=80.0和l=8。其中,阀值θj(j=1,2,3,4)的是对典型的棘波进行分析后,通过统计确定的;而选择ε=80是因为通常认为有诊断意义的棘波应该大于100μV。从图3可以看出,利用上述方法确定的局部极值能够准确地检测原始EEG信号中的棘波。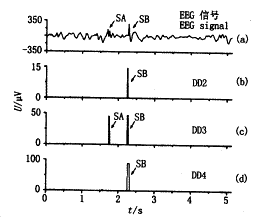
, 百拇医药
图3 (a)原始EEG信号s,(b)~(d)分别为尺度j=2,3,4上,与EEG信号s中棘波相关的细节的关周期平均振幅局部极值
Fig.3 (a) EEG signal S,(b)~(d) the local maximums of mean values between two cross-zeros of the details at the scales j=2,3,4 related to the spikes in EEG signal s
结果和讨论
采集了6位患者的脑电信号,从每一位患者的EEG记录中选出20个EEG信号片段,每段信号长度为5.12s(1024个样点),其中棘波由专家目视确定,然后利用本文提出的方法检测EEG信号中的棘波,检测结果见表1。
检测脑电中的癫痫样棘波,就是从背景EEG信号中检测具有某种特征的瞬态波形。自动检测棘波的主要的困难在于,这种瞬态波形和背景EEG信号的差别几乎是相对的,没有一个公认的、可以依据的检测标准。临床上一般认为,棘波是一种能够从相对变化缓慢的背景EEG中区分的、持续时间(during)在20~80ms之间的尖锐瞬态波形,只根据棘波的持续时间,可能会得到棘波的频率范围在12.5~50Hz之间。但是,对基底宽度在20~80ms之间的几种尖锐波形分析可知,有些波形的带宽还要大于12.5~50Hz。可以认为,相对于脑电的正常节律而言,棘波不仅具有瞬态性,而且还有宽带性。利用一个或几个带通滤波器,能够得到EEG信号在某些频带上的分量,但是,即使这些滤波器的带宽之和完全覆盖了癫痫脑电的频带范围,由于相位的原因,通过这些滤波器也不易观察同一时刻EEG信号在几个子频带或整个频带上的特性。由于棘波的瞬态性、宽带性和多态性,象本文中给出的检测方法那样,检测棘波时,经常需要考虑同一时刻EEG信号在几个子频带上的特性。因此,利用一个或几个彼此不相关的带通滤波器,有时难以判定某一时刻EEG信号中是否出现棘波。虽然,小波变换相当于用一组滤波器(filter bank)对信号进行滤波,但是,从本质上讲,小波变换是一种时频变换方法。与我们习惯的Cohen类时频分布不同的是,小波变换把信号变换到时间-尺度平面上,并且,在小尺度(对应高频)用短时间窗,在大尺度(对应低频)用长时间窗,不同尺度对应不同的频率分辨率,因此,利用小波变换,可以在不同分辨率下观察信号的特征。信号分解成小波级数后,各个尺度的带宽由所选用的小波基和信号的采样频率决定,对于本文所使用的正交小波基来说,当EEG信号的采样率为200Hz时,各尺度信号细节的3dB带宽见表2。进一步提高EEG信号的采样率,同样时间长度的采样信号,可以在更多的尺度上分解,但是,棘波可能占有的频带毕竟是有限的,考虑各个尺度的频带与小波基及信号采样率的关系,提高采样率应该对这种方法的检测结果不会有显著影响,对仿真信号的实验表明也是如此。由第1节(1)式可知,当EEG信号分解成小波级数后,原始信号等于各个尺度上信号分量的迭加,这意味着,某一时刻EEG信号的波形特征完全能够用这一时刻各个尺度上的子波形的集合表示,利用信号在同一时刻多个尺度上细节特征,可以比较全面刻画信号在该时刻的瞬态特征,因此,可以比较有效地检测EEG信号中与周围背景信号有显著差别的瞬态变化,并且,能准确地确定棘波出现的时间。另外,小波级数可以有效地计算,这一点对实际应用也很重要。我们的研究实践表明,利用小波级数自动检测棘波的方法有良好的应用前景。
, 百拇医药
表1 检测结果
Table 1 The results of spikes detection 实际棘波数
(total spikes)
检出棘波数
(detected spikes)
漏检
(undetected)
漏检率
(undetected rate)
误检
(error)
, 百拇医药
误检率
(error rate)
检测正确率
(correct rate)
177
183
15
8.47%
21
11.86%
79.66%
表2 尺度上细节的3dB带宽
, 百拇医药
Table 2 The 3 dB bandwidths of the details at the scales j=1,2,3,4 尺度(scales)(j)
1
2
3
4
3 dB带宽(bandwichs 3 dB)(Hz)
50~100
25~50
12.5~25
6.25~12.5
*基金项目:教育部博士点基金资助(97069837)
, 百拇医药
参考文献
[1] Smith JR. Automatic analysis and detection of EEG spikes[J].IEEE Trans. on BME,1974,21(1): 1~7
[2] Gevins AS.Automated analysis of the electrical activity of the human brain (EEG): a progress report[J]. Proc. of IEEE, 1975, 63(10): 1382~1399
[3] Bodenstein G. Feature extraction from the electroencephalogram by adaptive segmentation[J]. Proc. of IEEE, 1977, 65(5): 643~652
, http://www.100md.com
[4] Gevins AS. Analysis of the electromagnetic signal of the human brain: milestone, obstacle, and goals[J].IEEE Trans. on BME, 1984, 31(12): 833~850
[5] Wahlberg P,Salomonsson G.Feature extraction and clustering of EEG epileptic spike[J]. Computers and Biomedical Research, 1996, 29: 382~394
[6] Dandapat S and Ray GC.Spike detection in biomedical signals using midprediction filter[J]. Medical & Biological Engineering & Computing, 1997,35(4):354~360
, 百拇医药
[7] Morlet D et al. Wavelets analysis of high-resolution ECGs in post-infarction patients: role of the basic wavelet and of the analyzed lead[J]. International Journal of Bio-medical Computing, 1995, 39: 311~325
[8] Unser M. A review of wavelets in biomedical applications[J]. Proc. of IEEE, 1996, 84(4): 626~639.
[9] Mallat SG. A theory for multiresolution signal decomposition: The wavelet representation[J].IEEE Trans. on Pattern Analysis and Machine intelligence,1989, 11(7): 674~693
收稿日期:1998-06-22, 百拇医药
单位:宦飞 郑崇勋 西安交通大学生物医学工程研究所,西安 710049;黄远桂 第四军医大学西京医院,西安 710032)
关键词:小波级数;脑电图;癫痫;自动检测
航天医学与医学工程/990312摘要: 目的 研究自动提取癫痫脑电中棘波。 方法 把EEG信号分解成小波级数,在各个尺度上,利用信号细节在两个过零点之间的平均振幅确定瞬态波形的大小,通过选择平均振幅中的局部极值检测棘波。 结果 对6位患者的EEG信号进行处理,检测棘波的正确率为79.66%。 结论 这种方法能够比较准确地检测EEG中的棘波。
中图分类号: R318.03 文献标识码:A 文章编号:1002-0837(1999)03-0200-04
Detection of Spikes in Epileptic EEG by Using Wavelet Series.
, 百拇医药
HUAN Fei
Biomedical Engineering Institute, Xi'an
Jiaotong University, Xi'an 710049,China
ZHENG Chong-xun,HUANG Yuan-Gui.Space
Medicine & Medical Engineering,1999,12(3):200~203
Abstract: Objective To study automatic detection of the spikes in the epileptic EEG signals. Method Based on wavelet series decomposition of EEG signals, the mean amplitude between two cross-zeros of the detail signals at every scale was utilized to obtain quantitative values for the transient waves, and the abnormal spikes were distinguished from normal background EEG activities by the local maximum of the mean amplitudes of the different scales. Result The analysis of 6 patients' EEG data showed that the correctness ratio was 79.66% in detecting the spikes. Conclusion The epileptiform spikes in the abnormal EEG can be accurately detected with this method.
, 百拇医药
Key words: wavelet series;EEG;epilepsy;automatic detection
脑电图(EEG)中的瞬态特征往往具有重要的诊断意义,检测EEG信号中的瞬态特征波形对于诊断癫痫尤为重要。临床上有典型癫痫发作的患者,大部分可以在EEG检查中发现癫痫样特征波形(癫痫波)。癫痫波主要有以下几种:棘波(或尖波)、棘(或尖)慢复合波、以及多棘波群等。因此,癫痫脑电的检测,主要是EEG信号中棘波的检测。从60年代起,棘波的自动检测技术就受到了注意,许多学者在这一领域做了大量的研究,提出了多种方法[1~6]。然而,到目前为止,这一领域仍然没有取得重大进展。近年来,小波变换技术已在生物信号的处理领域得到广泛的应用[7,8]。本文利用小波变换方法的特点,设计了一个使用小波级数检测EEG中癫痫样棘波的方法。
数据采集
EEG数据采自在西京医院神经内科脑电图和脑地形图室作临床检查的患者。使用的脑电放大器是Chocolate 8816型,滤波器的通带为0.15~60 Hz,A/D转换器12位,采样率为200 Hz。使用头皮电极记录脑电,电极安放采用国际标准10-20连接方式,以双耳作为参考电极,前额为地电极,同时记录16导脑电数据。在检验过程中,采用睁眼闭眼、过度换气和美解眠药物注射三种方式诱发癫痫性放电。
, http://www.100md.com
小波级数的计算
信号x[n],n=0,1,…N,在尺度j=1,2,…,J(J≤M)上的小波级数为:
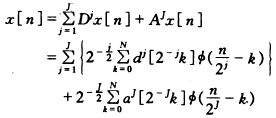 (1)
(1)其中,Djx[n]和Ajx[n]分别是信号x[n]在尺度j上的逼近和细节。本文使用三次B-样条生成的正交小波基[9]计算EEG信号的小波级数。
棘波检测
下面,分析如何利用小波级数检测EEG中的棘波。一段长度N=1024个样点(5.12s)的EEG信号s中含有两个棘波,分别记为SA和SB,如图1(a)所示。把s分解成4个尺度j=1,2,3,4上的小波级数,在尺度j=1,2,3,4上s的细节分别记为D1、D2、D3和D4,如图1(b)、(c)、(d)和(e)所示。图1(f)是s在尺度上的逼近A4。从图1(b)、(c)、(d)和(e)中可以看出,对应信号s中棘波SA和SB出现的时刻,在细节D1、D2、D3和D4中呈现高幅振荡,在尺度j=2,3,4上尤为明显,见图1(c)、(d)和(e)。

, 百拇医药
图1 (a)原始EEG信号s,(b)~(e)s的细节D1、D2、D3和D4,(f)s的逼近A4
Fig.1 (a) EEG signal s, (b)~(e) detailed D1, D2, D3, and D4 of s, (f) approximation A4 of s
在任一个尺度上,我们使用两个过零点之间的平均振幅,相当于半个周期里的平均振幅,度量信号细节的震荡大小。这样做的好处是,当某个时间间隔里,细节中含有多个高幅震荡时,平均振幅只有一个极值,并且,这个极值对应震荡最大的半个周期,而震荡最大的半周期恰好就是原始EEG信号中棘波峰值所在的时间间隔。
对图1(a)中的s,分别计算尺度j=1,2,3,4上细节的半周期平均振幅,并且记为MD1、MD2、MD3和MD4,见图2(b)~(e)。从图2(c)、(d)和(e)可以看出,对应SA和SB出现的时刻,在MD2、MD3和MD4中出现比较显著的局部极大值。这样,可以根据某一时刻、某些尺度上细节的半周期平均振幅的局部极大值,利用某种算法检测EEG信号中的棘波。

, 百拇医药
图2 (a)原始EEG信号s,(b)~(e)s在尺度j=1,2,3,4上的细节的半周期平均振幅MD1、MD2、MD3和MD4
Fig.2 (a) EEG signal s, (b)~(e) the mean values between two cross-zeros MD1, MD2, MD3, and MD4 of the details at the scales j=1,2,3,4 of s
下面给出具体的检测方法。
(1)计算局部极值
假设{aj0,aj1,…ajN-1}是尺度j上信号细节的半周期平均振幅序列,对于任一个点n,{ajn-l,…,ajn-1,ajn,ajn+l}是以n为中心,长度为2l+1的一个子序列,利用不等式,Ajn=ajn,如果ajn=max{ajn-l,…,ajn-1,ajn,ajn+l} (2a)
, http://www.100md.com
Ajn=0,如果ajn≠max{ajn-l,…,ajn-1,ajn,ajn+l} (2b)
产生一个新序列Ajn(0≤n≤N-1,显然Ajn≠0,如果,则在n点出现局部极值。这里,取l=2j-1/2*8当采样率为200 Hz时,8个样点相当于40 ms)。
(2)计算Ajn中所有不相同的极值{bj0,bj1,…bjM}的均值mbj。
, http://www.100md.com
(3)选择与棘波相关的局部极值
a.如果Ajn>=mbj,Bjn=Ajn,否则Bjn=0。得到Bj0,Bj1,…BjN-1;
b. 在尺度j=1,2,3,4上,给定适当的阀值θj,j=1,2,3,4。如果Bjn≥θj,,则Sjn=Bjn;当时Bjn<θj,如果在至少两个其它尺度上,在区间[n-l,n+l]内包含不为零的Bjn(i≠j),则取Sjn=Bjn;否则取Sjn=0;
, http://www.100md.com
c.如果Sjn>0,原始EEG信号在区间[n-l,n+l]内的幅值的绝对值的最大值的小于某个阀值ε,则取Sjn=0。
经过上述步骤后,以尺度j=2,3,4上的序列{Sjn}作为与棘波相关的局部极值,根据这些局部极值检测EEG信号中的棘波。图3给出了利用小波级数检测信号中sn棘波的结果。检测选用的参数为:θ1=6.25,θ2=12.5,θ3=25.0,θ4=50.0,ε=80.0和l=8。其中,阀值θj(j=1,2,3,4)的是对典型的棘波进行分析后,通过统计确定的;而选择ε=80是因为通常认为有诊断意义的棘波应该大于100μV。从图3可以看出,利用上述方法确定的局部极值能够准确地检测原始EEG信号中的棘波。

, 百拇医药
图3 (a)原始EEG信号s,(b)~(d)分别为尺度j=2,3,4上,与EEG信号s中棘波相关的细节的关周期平均振幅局部极值
Fig.3 (a) EEG signal S,(b)~(d) the local maximums of mean values between two cross-zeros of the details at the scales j=2,3,4 related to the spikes in EEG signal s
结果和讨论
采集了6位患者的脑电信号,从每一位患者的EEG记录中选出20个EEG信号片段,每段信号长度为5.12s(1024个样点),其中棘波由专家目视确定,然后利用本文提出的方法检测EEG信号中的棘波,检测结果见表1。
检测脑电中的癫痫样棘波,就是从背景EEG信号中检测具有某种特征的瞬态波形。自动检测棘波的主要的困难在于,这种瞬态波形和背景EEG信号的差别几乎是相对的,没有一个公认的、可以依据的检测标准。临床上一般认为,棘波是一种能够从相对变化缓慢的背景EEG中区分的、持续时间(during)在20~80ms之间的尖锐瞬态波形,只根据棘波的持续时间,可能会得到棘波的频率范围在12.5~50Hz之间。但是,对基底宽度在20~80ms之间的几种尖锐波形分析可知,有些波形的带宽还要大于12.5~50Hz。可以认为,相对于脑电的正常节律而言,棘波不仅具有瞬态性,而且还有宽带性。利用一个或几个带通滤波器,能够得到EEG信号在某些频带上的分量,但是,即使这些滤波器的带宽之和完全覆盖了癫痫脑电的频带范围,由于相位的原因,通过这些滤波器也不易观察同一时刻EEG信号在几个子频带或整个频带上的特性。由于棘波的瞬态性、宽带性和多态性,象本文中给出的检测方法那样,检测棘波时,经常需要考虑同一时刻EEG信号在几个子频带上的特性。因此,利用一个或几个彼此不相关的带通滤波器,有时难以判定某一时刻EEG信号中是否出现棘波。虽然,小波变换相当于用一组滤波器(filter bank)对信号进行滤波,但是,从本质上讲,小波变换是一种时频变换方法。与我们习惯的Cohen类时频分布不同的是,小波变换把信号变换到时间-尺度平面上,并且,在小尺度(对应高频)用短时间窗,在大尺度(对应低频)用长时间窗,不同尺度对应不同的频率分辨率,因此,利用小波变换,可以在不同分辨率下观察信号的特征。信号分解成小波级数后,各个尺度的带宽由所选用的小波基和信号的采样频率决定,对于本文所使用的正交小波基来说,当EEG信号的采样率为200Hz时,各尺度信号细节的3dB带宽见表2。进一步提高EEG信号的采样率,同样时间长度的采样信号,可以在更多的尺度上分解,但是,棘波可能占有的频带毕竟是有限的,考虑各个尺度的频带与小波基及信号采样率的关系,提高采样率应该对这种方法的检测结果不会有显著影响,对仿真信号的实验表明也是如此。由第1节(1)式可知,当EEG信号分解成小波级数后,原始信号等于各个尺度上信号分量的迭加,这意味着,某一时刻EEG信号的波形特征完全能够用这一时刻各个尺度上的子波形的集合表示,利用信号在同一时刻多个尺度上细节特征,可以比较全面刻画信号在该时刻的瞬态特征,因此,可以比较有效地检测EEG信号中与周围背景信号有显著差别的瞬态变化,并且,能准确地确定棘波出现的时间。另外,小波级数可以有效地计算,这一点对实际应用也很重要。我们的研究实践表明,利用小波级数自动检测棘波的方法有良好的应用前景。
, 百拇医药
表1 检测结果
Table 1 The results of spikes detection 实际棘波数
(total spikes)
检出棘波数
(detected spikes)
漏检
(undetected)
漏检率
(undetected rate)
误检
(error)
, 百拇医药
误检率
(error rate)
检测正确率
(correct rate)
177
183
15
8.47%
21
11.86%
79.66%
表2 尺度上细节的3dB带宽
, 百拇医药
Table 2 The 3 dB bandwidths of the details at the scales j=1,2,3,4 尺度(scales)(j)
1
2
3
4
3 dB带宽(bandwichs 3 dB)(Hz)
50~100
25~50
12.5~25
6.25~12.5
*基金项目:教育部博士点基金资助(97069837)
, 百拇医药
参考文献
[1] Smith JR. Automatic analysis and detection of EEG spikes[J].IEEE Trans. on BME,1974,21(1): 1~7
[2] Gevins AS.Automated analysis of the electrical activity of the human brain (EEG): a progress report[J]. Proc. of IEEE, 1975, 63(10): 1382~1399
[3] Bodenstein G. Feature extraction from the electroencephalogram by adaptive segmentation[J]. Proc. of IEEE, 1977, 65(5): 643~652
, http://www.100md.com
[4] Gevins AS. Analysis of the electromagnetic signal of the human brain: milestone, obstacle, and goals[J].IEEE Trans. on BME, 1984, 31(12): 833~850
[5] Wahlberg P,Salomonsson G.Feature extraction and clustering of EEG epileptic spike[J]. Computers and Biomedical Research, 1996, 29: 382~394
[6] Dandapat S and Ray GC.Spike detection in biomedical signals using midprediction filter[J]. Medical & Biological Engineering & Computing, 1997,35(4):354~360
, 百拇医药
[7] Morlet D et al. Wavelets analysis of high-resolution ECGs in post-infarction patients: role of the basic wavelet and of the analyzed lead[J]. International Journal of Bio-medical Computing, 1995, 39: 311~325
[8] Unser M. A review of wavelets in biomedical applications[J]. Proc. of IEEE, 1996, 84(4): 626~639.
[9] Mallat SG. A theory for multiresolution signal decomposition: The wavelet representation[J].IEEE Trans. on Pattern Analysis and Machine intelligence,1989, 11(7): 674~693
收稿日期:1998-06-22, 百拇医药