体液[Ca++]o变化诱发的心脏起搏细胞兴奋节律的分叉与混沌(Chay模型)
作者:古华光 任维 姜世忠
单位:古华光,任维,姜世忠(航天医学工程研究所,北京 100094)
关键词:体液;电解质代谢;心脏;细胞;节律;分叉现象;混沌
航天医学与医学工程/990309摘要: 目的 探讨航天中体液电解质中[Ca++]o变化对心跳节律的影响。方法 应用可兴奋性细胞离子通道最小模型—柴(Chay)模型,以心脏细胞动作电位峰-峰间期(ISI)为研究对象,调节方程中的参数Vc,(与[Ca++]o有关), 观察ISI的变化。 结果 ISI出现周期运动、混沌运动及加周期、倍周期分叉等现象,表明航天中[Ca++]o变化可能会引起心脏起搏细胞兴奋节律的变化,并进而使心跳节律发生相应变化。 结论 除心脏活动的神经、体液调节因素作用以外,航天中体液[Ca++]o的变化是引起心脏起搏细胞兴奋节律改变及其心律失常的不可忽视的因素。
, http://www.100md.com
中图分类号:R852 文献标识码:A 文章编号:1002-0837(1999)03-0188-05
Bifurcation and Chaos of Heart Cell Pacing Rhythm Evoked by Changing
[Ca++]o in Body Fluid.
GU Hua-guang,Institute of Space Medico-Engineering,Beijing 100094,China
REN Wei,JIANG Shi-Zhong.Space Medicine & Medical Engineering,1999,12(3):188~192
Abstract: Objective To study the effect of changes of electrolyte concentration on heart cell pacing rhythm. Method The minimal model of gating mechanism for ionic channels of exciting cells was used in this study.ISI(interspike interval) is regarded as the key parameter. Result ISI appears period, chaos, period adding bifurcation and period doubling bifurcation when Vc, a parameter related to [Ca++]o,was adjusted. Conclusion The results reveal that changes of [Ca++]o may evoke changes of rhythm of heart pacemaker cells. This implies that changes of [Ca++]o of body fluid are a cause influencing pacing rhythm of pacemaker cells and cardiac arrhythmia besides the neuro-humoral regulation,which should not be ignored.
, http://www.100md.com
Key words:body fluids;electrolyte metabolism;heart;cells;rhythm;bifurcation;chaos
航天中,[K+]、[Na+]、[Ca++]浓度都会发生变化,而[Ca++]o(细胞外体液中)的变化更有特殊的原因和意义。骨钙丢失、粪便和尿液中钙排除量的增加,均表明[Ca++]o的变化[1]。[Ca++]o的变化是否会是引起心律失常的因素呢?本文以非线性离子通道最小模型柴(Chay)模型为基础,研究模型中参数vc(与[Ca++]o有关的)变化时心脏细胞动作电位节律(即动作电位峰峰间期—interspike interval ISI)的变化, 探讨航天中[Ca++]o变化对心脏搏动节律的影响。
, http://www.100md.com
模型与分析
柴(Chay)模型 柴模型是柴建立的适合于Ca++起重要作用的可兴奋性细胞(如肌肉细胞和胰岛细胞)的普适模型[2]。在该模型中,主要有三个离子通道,Na+和Ca++通道,K+通道,电导依赖于[Ca++]i(细胞内)的K+通道,方程如下:
dV/dt=gim∞3h∞(vI-V)+gkvn4(vk-V)+gkcC/(1+C)(vk-V)+gL(vl-V) (1)
, http://www.100md.com
dn/dt=(n∞-n)/τ (2)
dC/dt =ρ(m∞3h∞(vc-V)-kcC) (3)
(1) 式右边4项分别为Na+-Ca++通道、K+通道、电导依赖于[Ca++]i的K+通道电流和漏电流,vI, vk, vl,V分别表示Na+-Ca++通道、K+通道、漏电流的电位和平衡电位,gi, gkv, gkc, gL分别代表各通道的最大电导,m∞和h∞为Na+-Ca++通道中两种门打开的概率。(2)式表示K+通道门打开概率的变化规律(n),τ是弛豫时间,n∞是n的稳定值。(3)式表示[Ca++]i变化规律,vc是Ca++可逆电位,式中两项分别表示进、出膜的Ca++流。C表示[Ca++]i除以离解常数。参数全部采用柴给出的数据。
, 百拇医药
柴模型是普适模型,它不涉及细胞的特性离子通道,可以用来模拟多种兴奋细胞的电活力;虽然该模型不针对心脏细胞的离子通道特性,但可以模拟心肌细胞(也可以是其它细胞)的自动兴奋节律。
在本文中,利用柴模型模拟心脏细胞兴奋节律,将vc作为调节参数, 研究对象是动作电位峰峰间期(ISI)。在本文中,除去文献列出的结果,所有数据图表都是本文得出的结果。
ISI的数值积分 调节与[Ca++]o有关参数vc,采用变步长4阶Runge-Kutta积分,对方程进行数值积分求解出动作电位,然后求出动作电位峰峰间期(ISI)。ISI的值为数值积分中的步长的倍数。
ISI的分析方法 本文采用的分析方法有非线性预测、李雅普诺夫指数和回归映象等。
非线性预测 非线性预测是分析数据序列是否混沌态的有效工具之一。混沌运动对初值敏感,长期运动不可预测而短期运动可以预测。针对这一特点,非线性预测计算当前相空间与以后相空间的相关系数;若得出的相关系数接近于1,是可以预测的,接近于0表示不可预测。详细的算法参见Sugihara G.的文献[3]。若数据序列短期可以预测而长期不可预测,可以认为该序列是混沌的。
, 百拇医药
数据替代 本文数据替代算法如下:对原始数据按随机数发生器产生高斯白噪声的顺序排列,新的数据序列即为替代数据。该数据序列傅利叶功率谱幅度分布于原始序列相同,分布规律与高斯白噪声相同[4]。
李雅普诺夫指数 李雅普诺夫指数是混沌运动的判据之一,它反应初始靠近的两个轨道(或点)随时间分离的程度。对于单一的时间序列,也可以求它的李雅普诺夫指数,可参见Wolf的算法[5]。若李雅普诺夫指数 (1)>0,表明是混沌运动;(2)<0,则是定常运动,不动点;(3)=0,周期运动;(4)趋于∞,随机运动。
回归映像 本文回归映像的算法如下:对原始序列X(n)(n=1~N),以(X(i),X(i+1))(i=0~N-1)为坐标在X-Y平面内画点。周期运动序列的映像为有限个孤立的点,而混沌态序列的映像为单峰映像[6]。
结 果
, http://www.100md.com
vc从100降低到0,步长为1的ISI有周期运动、混沌运动和分叉现象(见图1)。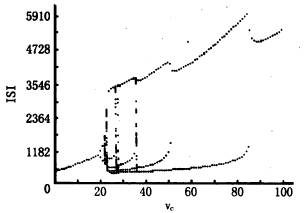
图1 ISI随vc变化全貌图
Fig.1 General figure of the changes of ISI following vc
ISI的加周期分叉现象 如图1所示,vc=86~100、vc=51~86、vc=37~51、vc=29~35、vc=24~26分别为周期1~周期5,呈现出加周期分叉现象。在周期3到周期4(vc=36附近)(如图2中的右图)、周期4到周期5(vc=27~28附近)(如图2中的左图)过程中存在混沌运动,如图2。而混沌中有周期5(vc=28.00~28.30)运动(见图2中的左图)。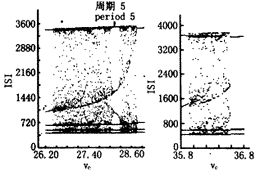
, http://www.100md.com
图2 vc=27和vc=36附近ISI随vc变化图
Fig.2 Periodic adding bifurcation of vc=27 and vc=36
ISI的倍周期分叉现象 vc=0~19为周期一运动,vc=19~24出现倍周期分叉到混沌,如图3所示。表1列出了Chay模型和逻辑方程f(x)=(x(1-x))倍周期分叉中(Tn-Tn-1)/(Tn+1-Tn)(Tn为周期n-1分叉到周期n时自变量的值,本文中自变量为vc)的值,两者差异不大,与费根鲍姆常数4.669也相当接近,因此vc=19~22时为倍周期分叉现象。在vc=23~24时ISI为混沌态时,并不是完全杂乱无章的,有周期三(如图3所示)、周期五运动存在。
, http://www.100md.com
图3 vc=19~24 ISI倍周期分叉到混沌
Fig.3 Periodic doubling bifurcation to chaos vc=19~24
表1 Chay模型和逻辑方程分叉过程中的(Tn-Tn-1)/(Tn+1-Tn)
Table 1 (Tn-Tn-1)/(Tn+1-Tn) of bifurcation of mathematic model proposed by Chay and logistical equations n
Tn(Chay模型)
, 百拇医药
(model)
(Tn-Tn+1)/(Tn+1-Tn)
(Chay模型
model)
逻辑方程
(logistical
equations)
1(1~2)
19.583
2(2~4)
21.168
, 百拇医药
5.266
4.751
3(4~8)
21.469
4.703
4.656
4(8~16)
21.533
4.573
4.668
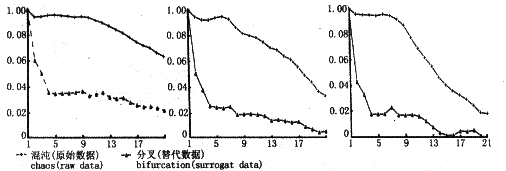
混沌态 如图4所示,vc=23、27和36时洛伦兹回归映像为尖峰形和马蹄形(与图4的第二排自左至右分别对应);vc=23、27和36时替代数据短期、长期预测相关系数都接近于0,不可预测;原始ISI预测的短期、长期相关系数分别接近于1和0,短期运动规律可以预测,长期不可预测(与图4的第二排自左至右分别对应);李雅普诺夫指数分别为0.607±0.065、0.491±0.120和0.340±0.127,都大于0;因此,vc=23、27和36时ISI为混沌态。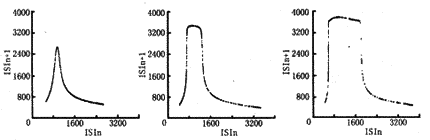
, 百拇医药
图4 vc=23、vc=27和vc=36 时的回归映像、重构吸引子和原始数据、替代数据非线性预测
Fig.4 Return map nonlinear forecasting of raw data and surrogate data, of vc=23,vc=27 and vc=36 周期运动 vc=99,vc=80,vc=40,vc=33和vc=25时分别为周期1、2、3、4及5,如图5所示。从重构吸引子([Ca++]i为纵标V的横标画点)可以看出C-V的运行轨道为闭曲线,并且是随周期重叠的(图5第二排分别对应vc=99、80、40、33和25的吸引子);回归映像为离散的点,点数与周期数相同(图5第一排分别对应vc=80、40、33和25的回归映像)。可见,周期运动与混沌运动明显不同。
, 百拇医药
图5 vc=99,vc=80,vc=40,vc=33和vc=25,vc=80时的重构吸引子vc=40,vc=33和vc=25时的回归映像
Fig.5 Limit circle orbit in Ca-V plane of vc =99, vc= 80,vc=40,vc=33 and vc=25,the return map and of vc= 80,vc=40,vc=33 and vc=25
讨 论
, http://www.100md.com
柴模型中,vc是Ca++依赖性K+通道的可逆电位,与离子通道的活性和[Ca++]o有关。而航天过程中,航天员骨质脱钙、粪便和尿中排出钙离子浓度增加,表明[Ca++]o有变化,进而导致[Ca++]i发生变化,这必定导致vc发生变化。
柴模型表明,ISI随vc的变化呈现出复杂的变化。ISI呈现出周期运动、混沌运动和分叉过程。ISI的变化使得心跳节律相应改变。若航天中[Ca++]o处在使ISI处于周期运动状态的水平上,ISI则会出现周期运动,进而心跳节律也为周期运动;因此,航天中航天员出现的二联律或三联率,可能是[Ca++]o变化引起的。[Ca++]o可在很大范围内(vc=24~100)使得ISI处于周期运动;在ISI的倍周期分叉过程中,ISI也会出现周期运动;而在混沌“带”中,也有周期运动的窗口存在;这完全有可能引起ISI的周期二或周期三运动,使得心脏搏动节律由在地面的混沌状态变化到飞行中的周期二或周期三状态。例如,“阿波罗15”有一名航天员出现多个二联律,当时认为可能与食物中缺钾和疲劳有关。该航天员返回地面后经21个月查出有心脏病并由此认定二联律与此有关[7]。但是,现在看来,二联律的出现可能就是电解质离子(如钙离子、钾离子)浓度的变化或其它因素引起的。前苏联的“联盟TM2-和平号”航天员拉韦金在舱外活动时出现了三联律期前收缩[7],也可能与此有关。
, http://www.100md.com
此外,vc随时间会有一定幅度的涨落。若vc使得ISI在分叉点附近,vc的微小涨落可能会导致ISI在周期运动态和混沌运动态之间转换;若vc使得ISI在混沌带内,vc的微小涨落可能会导致ISI也会出现复杂变化;而混沌运动又具有对初始条件敏感的特性,因此,ISI势必会出现复杂的变化;进而使得心跳节律出现复杂变化,这可能是航天中心律失常的原因之一。
菲茨赫(Fitzhugh)在范德玻尔方程基础上,将心脏作为一个整体进行了非线性模型研究,得出了大体象心电图的振荡;但没有涉及心脏各部位所起的作用不同,没有涉及心脏振荡的实质。毕勒(Beeler)-路特(Reuter)在H-H方程[8]基础上,用非线性离子通道方法研究了心脏细胞动作电位,该模型能较好地描述心室肌细胞动作电位。但都没有对ISI进行分析,没有对心跳节律进行研究[9]。格拉斯(Glass)用周期驱动的非线性振子模型,研究了脉冲电流刺激下离体培养的心肌细胞团的跳动节律,当脉冲电流频率倍周期增加时,发现了心肌细胞搏动节律锁相到脉冲电流的频率上[10]。但格拉斯研究的是电流激励下的心肌细胞,不是正常生理条件下的心肌细胞。格拉斯和本文的结果表明:心跳节律可能在混沌运动与周期运动转换,呈现出复杂的变化,这可能是心律失常的原因之一。
, 百拇医药
柴在该模型的研究中,将gkc作为可调参数,研究膜电位、离子浓度等随时间的变化,得出了周期1、2、4、8、12等,并出现了混沌。任维等[11]将柴模型应用于神经细胞放电节律的研究,计算机模拟结果和实验结果相符和。这表明柴模型应用于可兴奋性细胞的研究是可行的。本文结果对心跳节律的研究具有重要启发意义,尤其是载人航天中或[Ca++]o变化时心率失常的研究。当然,该结果有待于实验的进一步验证,心肌细胞的离体培养,调节培养液[Ca++]o,研究心脏细胞跳动节律可能是较好的实验方法。
航天中有些航天员出现心律失常、二联律或三联律,其可能因素是多方面的:可能是病理方面的,也可能是生理方面的。而本文结果表明电解质浓度的变化也可能是因素之一。目前,关于心脏跳动节律的研究,集中于神经调节方面,如心率变异性分析,但局限于实验数据的分析处理;或采用动态心电图,这些方法不能全面反应影响心脏跳动节律的因素。而关于体液调节、离子通道活性的变化和体液电解质浓度变化对心脏节律的影响的研究很少,柴模型十分简单,不是直接针对心脏细胞的非线性模型,也没有考虑心脏动作电位的具体过程,但得出了有很大启发性的结果。因此,建立非线性模型对心脏跳动节律进行研究势在必行。
, 百拇医药
对于心脏跳动节律的研究,应建立针对心脏细胞特点的、考虑心脏动作电位具体过程的非线性模型,还要考虑噪音的影响;在分析方法上也应有所改进,采用数值解法与微分方程定性解法相结合,或采用解析方法。
参考文献
[1] 庄祥昌,裴静琛.失重生理学[M].北京:人民军医出版社,1989:93~96
[2] Fan yin-shui, Chay TR. Generation of periodic and chaotic bursting in an excitable cell model[J].Biol. Cybern,1994,71(5):417~431
[3] Sugihara G, May RM. Nonlinear forecasting as a way of distinguishing chaos from measure error in time series[J]. Nature, 1990,344(6268):734
, http://www.100md.com
[4] Theiler J ,Eubank S, Longtin A et al. Testing for nonlinearity in time series : the method of surrogate data[J]. Physic D,1992,58:77
[5] Wolf A,Swift JB,Swinney HL et al.Determining lyapunov exponents from a time series[J]. Physic D ,1985,16:285~317
[6] 陈式刚.映象与混沌[M].北京:国防工业出版社,1995:24~35
[7] 刘光远,沈羡云,陈涤明. 重力生理学-理论与实践[M].北京:国防工业出版社,1993:184
[8] Hodgkin AL , Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. J Physiol,1952,117:500~544
, 百拇医药
[9] Beller GW,Reuter H. Reconstruction of the action potential of ventricular myocardial fibres[J].J Physiol, 1977,286(1):177~210
[10] Guevara MR , Glass L, Shrier A. Phase Locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cells[J]. Science, 1981,214(4527):1350~1352
[11] 任 维. 损伤神经自发放电节律变化的离子基础和非线性动力学机制:[博士论文][D].西安:第四军医大学,1996:6
收稿日期:1998-06-23, 百拇医药
单位:古华光,任维,姜世忠(航天医学工程研究所,北京 100094)
关键词:体液;电解质代谢;心脏;细胞;节律;分叉现象;混沌
航天医学与医学工程/990309摘要: 目的 探讨航天中体液电解质中[Ca++]o变化对心跳节律的影响。方法 应用可兴奋性细胞离子通道最小模型—柴(Chay)模型,以心脏细胞动作电位峰-峰间期(ISI)为研究对象,调节方程中的参数Vc,(与[Ca++]o有关), 观察ISI的变化。 结果 ISI出现周期运动、混沌运动及加周期、倍周期分叉等现象,表明航天中[Ca++]o变化可能会引起心脏起搏细胞兴奋节律的变化,并进而使心跳节律发生相应变化。 结论 除心脏活动的神经、体液调节因素作用以外,航天中体液[Ca++]o的变化是引起心脏起搏细胞兴奋节律改变及其心律失常的不可忽视的因素。
, http://www.100md.com
中图分类号:R852 文献标识码:A 文章编号:1002-0837(1999)03-0188-05
Bifurcation and Chaos of Heart Cell Pacing Rhythm Evoked by Changing
[Ca++]o in Body Fluid.
GU Hua-guang,Institute of Space Medico-Engineering,Beijing 100094,China
REN Wei,JIANG Shi-Zhong.Space Medicine & Medical Engineering,1999,12(3):188~192
Abstract: Objective To study the effect of changes of electrolyte concentration on heart cell pacing rhythm. Method The minimal model of gating mechanism for ionic channels of exciting cells was used in this study.ISI(interspike interval) is regarded as the key parameter. Result ISI appears period, chaos, period adding bifurcation and period doubling bifurcation when Vc, a parameter related to [Ca++]o,was adjusted. Conclusion The results reveal that changes of [Ca++]o may evoke changes of rhythm of heart pacemaker cells. This implies that changes of [Ca++]o of body fluid are a cause influencing pacing rhythm of pacemaker cells and cardiac arrhythmia besides the neuro-humoral regulation,which should not be ignored.
, http://www.100md.com
Key words:body fluids;electrolyte metabolism;heart;cells;rhythm;bifurcation;chaos
航天中,[K+]、[Na+]、[Ca++]浓度都会发生变化,而[Ca++]o(细胞外体液中)的变化更有特殊的原因和意义。骨钙丢失、粪便和尿液中钙排除量的增加,均表明[Ca++]o的变化[1]。[Ca++]o的变化是否会是引起心律失常的因素呢?本文以非线性离子通道最小模型柴(Chay)模型为基础,研究模型中参数vc(与[Ca++]o有关的)变化时心脏细胞动作电位节律(即动作电位峰峰间期—interspike interval ISI)的变化, 探讨航天中[Ca++]o变化对心脏搏动节律的影响。
, http://www.100md.com
模型与分析
柴(Chay)模型 柴模型是柴建立的适合于Ca++起重要作用的可兴奋性细胞(如肌肉细胞和胰岛细胞)的普适模型[2]。在该模型中,主要有三个离子通道,Na+和Ca++通道,K+通道,电导依赖于[Ca++]i(细胞内)的K+通道,方程如下:
dV/dt=gim∞3h∞(vI-V)+gkvn4(vk-V)+gkcC/(1+C)(vk-V)+gL(vl-V) (1)
, http://www.100md.com
dn/dt=(n∞-n)/τ (2)
dC/dt =ρ(m∞3h∞(vc-V)-kcC) (3)
(1) 式右边4项分别为Na+-Ca++通道、K+通道、电导依赖于[Ca++]i的K+通道电流和漏电流,vI, vk, vl,V分别表示Na+-Ca++通道、K+通道、漏电流的电位和平衡电位,gi, gkv, gkc, gL分别代表各通道的最大电导,m∞和h∞为Na+-Ca++通道中两种门打开的概率。(2)式表示K+通道门打开概率的变化规律(n),τ是弛豫时间,n∞是n的稳定值。(3)式表示[Ca++]i变化规律,vc是Ca++可逆电位,式中两项分别表示进、出膜的Ca++流。C表示[Ca++]i除以离解常数。参数全部采用柴给出的数据。
, 百拇医药
柴模型是普适模型,它不涉及细胞的特性离子通道,可以用来模拟多种兴奋细胞的电活力;虽然该模型不针对心脏细胞的离子通道特性,但可以模拟心肌细胞(也可以是其它细胞)的自动兴奋节律。
在本文中,利用柴模型模拟心脏细胞兴奋节律,将vc作为调节参数, 研究对象是动作电位峰峰间期(ISI)。在本文中,除去文献列出的结果,所有数据图表都是本文得出的结果。
ISI的数值积分 调节与[Ca++]o有关参数vc,采用变步长4阶Runge-Kutta积分,对方程进行数值积分求解出动作电位,然后求出动作电位峰峰间期(ISI)。ISI的值为数值积分中的步长的倍数。
ISI的分析方法 本文采用的分析方法有非线性预测、李雅普诺夫指数和回归映象等。
非线性预测 非线性预测是分析数据序列是否混沌态的有效工具之一。混沌运动对初值敏感,长期运动不可预测而短期运动可以预测。针对这一特点,非线性预测计算当前相空间与以后相空间的相关系数;若得出的相关系数接近于1,是可以预测的,接近于0表示不可预测。详细的算法参见Sugihara G.的文献[3]。若数据序列短期可以预测而长期不可预测,可以认为该序列是混沌的。
, 百拇医药
数据替代 本文数据替代算法如下:对原始数据按随机数发生器产生高斯白噪声的顺序排列,新的数据序列即为替代数据。该数据序列傅利叶功率谱幅度分布于原始序列相同,分布规律与高斯白噪声相同[4]。
李雅普诺夫指数 李雅普诺夫指数是混沌运动的判据之一,它反应初始靠近的两个轨道(或点)随时间分离的程度。对于单一的时间序列,也可以求它的李雅普诺夫指数,可参见Wolf的算法[5]。若李雅普诺夫指数 (1)>0,表明是混沌运动;(2)<0,则是定常运动,不动点;(3)=0,周期运动;(4)趋于∞,随机运动。
回归映像 本文回归映像的算法如下:对原始序列X(n)(n=1~N),以(X(i),X(i+1))(i=0~N-1)为坐标在X-Y平面内画点。周期运动序列的映像为有限个孤立的点,而混沌态序列的映像为单峰映像[6]。
结 果
, http://www.100md.com
vc从100降低到0,步长为1的ISI有周期运动、混沌运动和分叉现象(见图1)。

图1 ISI随vc变化全貌图
Fig.1 General figure of the changes of ISI following vc
ISI的加周期分叉现象 如图1所示,vc=86~100、vc=51~86、vc=37~51、vc=29~35、vc=24~26分别为周期1~周期5,呈现出加周期分叉现象。在周期3到周期4(vc=36附近)(如图2中的右图)、周期4到周期5(vc=27~28附近)(如图2中的左图)过程中存在混沌运动,如图2。而混沌中有周期5(vc=28.00~28.30)运动(见图2中的左图)。

, http://www.100md.com
图2 vc=27和vc=36附近ISI随vc变化图
Fig.2 Periodic adding bifurcation of vc=27 and vc=36
ISI的倍周期分叉现象 vc=0~19为周期一运动,vc=19~24出现倍周期分叉到混沌,如图3所示。表1列出了Chay模型和逻辑方程f(x)=(x(1-x))倍周期分叉中(Tn-Tn-1)/(Tn+1-Tn)(Tn为周期n-1分叉到周期n时自变量的值,本文中自变量为vc)的值,两者差异不大,与费根鲍姆常数4.669也相当接近,因此vc=19~22时为倍周期分叉现象。在vc=23~24时ISI为混沌态时,并不是完全杂乱无章的,有周期三(如图3所示)、周期五运动存在。

, http://www.100md.com
图3 vc=19~24 ISI倍周期分叉到混沌
Fig.3 Periodic doubling bifurcation to chaos vc=19~24
表1 Chay模型和逻辑方程分叉过程中的(Tn-Tn-1)/(Tn+1-Tn)
Table 1 (Tn-Tn-1)/(Tn+1-Tn) of bifurcation of mathematic model proposed by Chay and logistical equations n
Tn(Chay模型)
, 百拇医药
(model)
(Tn-Tn+1)/(Tn+1-Tn)
(Chay模型
model)
逻辑方程
(logistical
equations)
1(1~2)
19.583
2(2~4)
21.168
, 百拇医药
5.266
4.751
3(4~8)
21.469
4.703
4.656
4(8~16)
21.533
4.573
4.668
混沌态 如图4所示,vc=23、27和36时洛伦兹回归映像为尖峰形和马蹄形(与图4的第二排自左至右分别对应);vc=23、27和36时替代数据短期、长期预测相关系数都接近于0,不可预测;原始ISI预测的短期、长期相关系数分别接近于1和0,短期运动规律可以预测,长期不可预测(与图4的第二排自左至右分别对应);李雅普诺夫指数分别为0.607±0.065、0.491±0.120和0.340±0.127,都大于0;因此,vc=23、27和36时ISI为混沌态。


, 百拇医药
图4 vc=23、vc=27和vc=36 时的回归映像、重构吸引子和原始数据、替代数据非线性预测
Fig.4 Return map nonlinear forecasting of raw data and surrogate data, of vc=23,vc=27 and vc=36 周期运动 vc=99,vc=80,vc=40,vc=33和vc=25时分别为周期1、2、3、4及5,如图5所示。从重构吸引子([Ca++]i为纵标V的横标画点)可以看出C-V的运行轨道为闭曲线,并且是随周期重叠的(图5第二排分别对应vc=99、80、40、33和25的吸引子);回归映像为离散的点,点数与周期数相同(图5第一排分别对应vc=80、40、33和25的回归映像)。可见,周期运动与混沌运动明显不同。

, 百拇医药
图5 vc=99,vc=80,vc=40,vc=33和vc=25,vc=80时的重构吸引子vc=40,vc=33和vc=25时的回归映像
Fig.5 Limit circle orbit in Ca-V plane of vc =99, vc= 80,vc=40,vc=33 and vc=25,the return map and of vc= 80,vc=40,vc=33 and vc=25
讨 论
, http://www.100md.com
柴模型中,vc是Ca++依赖性K+通道的可逆电位,与离子通道的活性和[Ca++]o有关。而航天过程中,航天员骨质脱钙、粪便和尿中排出钙离子浓度增加,表明[Ca++]o有变化,进而导致[Ca++]i发生变化,这必定导致vc发生变化。
柴模型表明,ISI随vc的变化呈现出复杂的变化。ISI呈现出周期运动、混沌运动和分叉过程。ISI的变化使得心跳节律相应改变。若航天中[Ca++]o处在使ISI处于周期运动状态的水平上,ISI则会出现周期运动,进而心跳节律也为周期运动;因此,航天中航天员出现的二联律或三联率,可能是[Ca++]o变化引起的。[Ca++]o可在很大范围内(vc=24~100)使得ISI处于周期运动;在ISI的倍周期分叉过程中,ISI也会出现周期运动;而在混沌“带”中,也有周期运动的窗口存在;这完全有可能引起ISI的周期二或周期三运动,使得心脏搏动节律由在地面的混沌状态变化到飞行中的周期二或周期三状态。例如,“阿波罗15”有一名航天员出现多个二联律,当时认为可能与食物中缺钾和疲劳有关。该航天员返回地面后经21个月查出有心脏病并由此认定二联律与此有关[7]。但是,现在看来,二联律的出现可能就是电解质离子(如钙离子、钾离子)浓度的变化或其它因素引起的。前苏联的“联盟TM2-和平号”航天员拉韦金在舱外活动时出现了三联律期前收缩[7],也可能与此有关。
, http://www.100md.com
此外,vc随时间会有一定幅度的涨落。若vc使得ISI在分叉点附近,vc的微小涨落可能会导致ISI在周期运动态和混沌运动态之间转换;若vc使得ISI在混沌带内,vc的微小涨落可能会导致ISI也会出现复杂变化;而混沌运动又具有对初始条件敏感的特性,因此,ISI势必会出现复杂的变化;进而使得心跳节律出现复杂变化,这可能是航天中心律失常的原因之一。
菲茨赫(Fitzhugh)在范德玻尔方程基础上,将心脏作为一个整体进行了非线性模型研究,得出了大体象心电图的振荡;但没有涉及心脏各部位所起的作用不同,没有涉及心脏振荡的实质。毕勒(Beeler)-路特(Reuter)在H-H方程[8]基础上,用非线性离子通道方法研究了心脏细胞动作电位,该模型能较好地描述心室肌细胞动作电位。但都没有对ISI进行分析,没有对心跳节律进行研究[9]。格拉斯(Glass)用周期驱动的非线性振子模型,研究了脉冲电流刺激下离体培养的心肌细胞团的跳动节律,当脉冲电流频率倍周期增加时,发现了心肌细胞搏动节律锁相到脉冲电流的频率上[10]。但格拉斯研究的是电流激励下的心肌细胞,不是正常生理条件下的心肌细胞。格拉斯和本文的结果表明:心跳节律可能在混沌运动与周期运动转换,呈现出复杂的变化,这可能是心律失常的原因之一。
, 百拇医药
柴在该模型的研究中,将gkc作为可调参数,研究膜电位、离子浓度等随时间的变化,得出了周期1、2、4、8、12等,并出现了混沌。任维等[11]将柴模型应用于神经细胞放电节律的研究,计算机模拟结果和实验结果相符和。这表明柴模型应用于可兴奋性细胞的研究是可行的。本文结果对心跳节律的研究具有重要启发意义,尤其是载人航天中或[Ca++]o变化时心率失常的研究。当然,该结果有待于实验的进一步验证,心肌细胞的离体培养,调节培养液[Ca++]o,研究心脏细胞跳动节律可能是较好的实验方法。
航天中有些航天员出现心律失常、二联律或三联律,其可能因素是多方面的:可能是病理方面的,也可能是生理方面的。而本文结果表明电解质浓度的变化也可能是因素之一。目前,关于心脏跳动节律的研究,集中于神经调节方面,如心率变异性分析,但局限于实验数据的分析处理;或采用动态心电图,这些方法不能全面反应影响心脏跳动节律的因素。而关于体液调节、离子通道活性的变化和体液电解质浓度变化对心脏节律的影响的研究很少,柴模型十分简单,不是直接针对心脏细胞的非线性模型,也没有考虑心脏动作电位的具体过程,但得出了有很大启发性的结果。因此,建立非线性模型对心脏跳动节律进行研究势在必行。
, 百拇医药
对于心脏跳动节律的研究,应建立针对心脏细胞特点的、考虑心脏动作电位具体过程的非线性模型,还要考虑噪音的影响;在分析方法上也应有所改进,采用数值解法与微分方程定性解法相结合,或采用解析方法。
参考文献
[1] 庄祥昌,裴静琛.失重生理学[M].北京:人民军医出版社,1989:93~96
[2] Fan yin-shui, Chay TR. Generation of periodic and chaotic bursting in an excitable cell model[J].Biol. Cybern,1994,71(5):417~431
[3] Sugihara G, May RM. Nonlinear forecasting as a way of distinguishing chaos from measure error in time series[J]. Nature, 1990,344(6268):734
, http://www.100md.com
[4] Theiler J ,Eubank S, Longtin A et al. Testing for nonlinearity in time series : the method of surrogate data[J]. Physic D,1992,58:77
[5] Wolf A,Swift JB,Swinney HL et al.Determining lyapunov exponents from a time series[J]. Physic D ,1985,16:285~317
[6] 陈式刚.映象与混沌[M].北京:国防工业出版社,1995:24~35
[7] 刘光远,沈羡云,陈涤明. 重力生理学-理论与实践[M].北京:国防工业出版社,1993:184
[8] Hodgkin AL , Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. J Physiol,1952,117:500~544
, 百拇医药
[9] Beller GW,Reuter H. Reconstruction of the action potential of ventricular myocardial fibres[J].J Physiol, 1977,286(1):177~210
[10] Guevara MR , Glass L, Shrier A. Phase Locking, period-doubling bifurcations, and irregular dynamics in periodically stimulated cells[J]. Science, 1981,214(4527):1350~1352
[11] 任 维. 损伤神经自发放电节律变化的离子基础和非线性动力学机制:[博士论文][D].西安:第四军医大学,1996:6
收稿日期:1998-06-23, 百拇医药