伽玛刀剂量的Monte Carlo计算
作者:包尚联 郭景新 黄斐增 温琛林
单位:北京大学肿瘤物理诊疗技术研究中心, 北京大学重离子物理研究所, 北京100871
关键词:吸收剂量;Monte Carlo模拟;伽玛刀
中国医学物理学杂志990301 摘要:应用Monte Carlo模拟方法,计算了Leksell型的伽玛刀在人脑体模中的剂量分布曲线, 其中包括单源和多源情况。
中图分类号:R144 文献标识码:A 文章编号:1005-202X(1999)03-0129-03
MC calculation of γ-knife dose
BAO Shang-lian , GUO Jing-xin , WEN Chun-lin , HUANG Fei-zeng
, 百拇医药
(The Center for Radiological Science, The Institute of Heavy Ion Physics, Peking University,Beijing 100871,China)
Abstract: The dose distribution of Leksell type of γ-knife was simulated by Monte Carlo method for single 60Co source and the total 201 sources.
Key words: absorbing dose; monte Carlo simulation; γ-knife
前言:在肿瘤治疗方面,手术治疗、化学药物治疗和放射性治疗并列成为三种主要的治疗手段。放射治疗已经成为肿瘤必不可少的治疗手段之一。到目前为止,癌症的治愈率已经超过50%,其中放射治疗方法参与的病人在世界上,大约是60%,在中国达到70%左右。完全由放射线治愈的癌症病人大约在世界上已经达到25%[1]。为了在尽可能保护正常组织的情况下消灭肿瘤细胞,提高治疗肿瘤时对正常组织的保护,提高在肿瘤组织和正常组织中的剂量比(T/N比)是放疗追求的目标。多源立体定位的伽玛同位素放疗装置(伽玛刀)就是用于达到这个目的而设计的同位素治疗装置,是“钴炮”等这类治疗装置的发展。
, 百拇医药
在进行放射治疗剂量学研究应该包括两个方面和三种手段。两个方面是指宏观剂量和微观剂量的问题;三种手段是指解析方法计算、Monte Carlo (MC) 计算和实验测量。由于计算速度的问题,临床上使用的剂量计算方法是近似的解析计算方法,这种计算方法速度快,但是准确性差,必须加上各种修正,这些修正量是通过MC计算得到的,为了准确起见,MC计算需要尽可能好的实验验证,至少在相对计算的基础上,测量若干个实验值作为绝对定标。
近几年来, 国内伽玛刀技术和临床应用发展得很快,临床上使用的伽玛刀已达13台之多,而且还有增加的趋势。目前世界上伽玛刀的剂量计算大多采用Leksell gamma unit的Kula治疗计划系统[2]中的剂量计算方法。其剂量计算采用单源效果累加的方法实现。在靶点处,该方法把靶物质分成若干个小体积元,小体积元的总数为33×33×33个,其边长根据肿瘤的大小进行调整。其剂量计算是按均匀介质模型进行的。实际上这个方法有改进和进一步研究的必要。 本文介绍了用MCNP3.0a的早期版本进行MC模拟计算的结果。我们计算了在单源情况下和多源情况下的等位剂量分布曲线,及其剂量计算中粒子能量的展宽函数。目前的计算结果用Leksell Gamma Unit在相同条件下提供的数据相同(有意识的比较),以此为基础,进行了别的剂量学方面的模拟计算。这些工作为我们深入开展放疗剂量学研究和微机编程打下了基础。
, http://www.100md.com
1 原理和方法
现有的伽玛刀用的同位素是60Co放射源,其能量比较单一,在Monte Carlo计算时,对源分布的模拟是比较容易的。主要的改进,是要增加一个对治疗系统几何结构模拟的程序, 这个程序是我们自己编写的。在计算中,光子和物质相互作用过程中主要考虑了相干散射、非相干散射、光电效应、电子对效应。实际上,由于伽玛能量比较低,电子对效应基本可以忽略。相干散射发生在低能端,主要是模拟光子在介质中改变方向的飞行,光子在靶物质中没有能量沉积;非相干散射中产生的电子,无论能量多大,都作就地能量沉积处理;发生光电效应时考虑了荧光发射和内转换电子;发生电子对效应时,产生正负电子,其动能就地积沉,正负电子湮灭产生的2个伽玛光子,在模拟中被继续跟踪。通过以上机制计算在脑肿瘤周围的能量沉积,经计算转换成吸收剂量[3]。
2 对单源的模拟
在使用剂量叠加方法时,对单个60Co放射源的模拟是整个剂量计算的核心问题。模拟时,假定伽玛光子从Z轴正方向垂直入射,几何块为长和宽都为16cm有一定厚度的长方体,剂量计算Z方向的步长为1mm,几何块1为靶点位置,点源S到靶点位置的距离为40.1cm,皮肤表面到靶点的距离为5.0cm。几何块51为空气隔层,几何块1~50的靶物质填充为脑组织。
, 百拇医药
在空气隔层的上方为一个带锥形准直器的铅屏蔽体,其准直孔径同Leksell Gamma Unit相同。以靶点为中心,大小为1mm×1mm×1mm的体积元,共40×40个;从皮肤到肿瘤的位置,沿z方向也分成1mm×1mm×1mm的体积元,共40×50个。按此简化模型,我们分别模拟了18mm、14mm、8mm、4mm四种准直孔径的结果。以8mm孔径为例的计算几何结构如图1的单源几何模型所示,其模拟的计算结果示于图2。
图1 单源几何结构示意图。
图2 8mm孔径的等剂量曲线(a: x-y平面;b: x-z平面)
图2a中的等剂量曲线以中心的剂量为最大,由内向外的剂量从90%逐步递减到10%。图2b的等剂量曲线由上向下从90%逐步递减到50%。我们定义伽玛刀的锐度作为剂量在肿瘤和正常组织分界处变化速度快慢的物理量。它表示组织中的吸收剂量从90%降到10%时的空间距离。由上图2a可见,8mm准直器在单源情况下的锐度为1.5mm。
, 百拇医药
3 多源情况下的模拟
由于Leksell伽玛刀共有201个放射源,分布在5个环带上,各个环带上有44、44、40、38、35个准直器,如图3a所示。头部模型采用椭球形,如图3b,三层椭球由外向内填充皮肤、骨胳、脑组织等成份。靶点位置选在距椭球中心4.5cm处,距皮肤表面5cm处。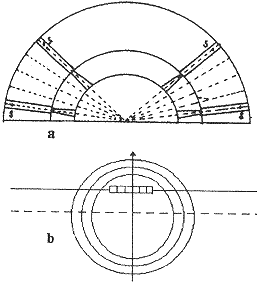
图3 a放射源和准直器模型,b头部模型(注:图3a中只画出了五个环带中两个)
根据上述模型,模拟结果如图4。
图4 8mm孔径的等剂量曲线(a: x-y平面;b: x-z平面)
, http://www.100md.com 图4中等剂量曲线中的等剂量曲线的剂量从中心点开始由内向外从90%降到10%。由上图可知,其锐度比单源情况大,为7.3mm,这是因为各路伽玛光子交叉处形成的半影,使得剂量分布的锐度减低。计算结果还表明,半剂量曲线的宽度在x、y、z三个轴上分别为11.3、11.3、9.3,同文献[1]中给出的实验数据大体相同。我们按照同样方法还计算了4mm,14mm,188mm准直器的剂量分布,其半剂量曲线的宽度分别为6.0mm,19.5mm,25.0mm。相应的锐度分别为3.5mm,12.0mm,和12.1mm。
基金项目:北京自然科学基金和国家教育部黄斐增回国人员基金资助项目
参考文献:
[1] Advances in Hydrotherapy, Edited by Ugo Amaidi et al., Press. Elsevier 1997.
[2] User's manual of Leksell Gamma Unit,Elekta Edition, April 1992.
[3] Kindl, et al. Z. Med. Phys.4(1994)215-219.
[4] 郭景新.伽玛刀剂量的Monte Carlo 模拟[D]. 1998.
收稿日期:1998-12-14, http://www.100md.com
单位:北京大学肿瘤物理诊疗技术研究中心, 北京大学重离子物理研究所, 北京100871
关键词:吸收剂量;Monte Carlo模拟;伽玛刀
中国医学物理学杂志990301 摘要:应用Monte Carlo模拟方法,计算了Leksell型的伽玛刀在人脑体模中的剂量分布曲线, 其中包括单源和多源情况。
中图分类号:R144 文献标识码:A 文章编号:1005-202X(1999)03-0129-03
MC calculation of γ-knife dose
BAO Shang-lian , GUO Jing-xin , WEN Chun-lin , HUANG Fei-zeng
, 百拇医药
(The Center for Radiological Science, The Institute of Heavy Ion Physics, Peking University,Beijing 100871,China)
Abstract: The dose distribution of Leksell type of γ-knife was simulated by Monte Carlo method for single 60Co source and the total 201 sources.
Key words: absorbing dose; monte Carlo simulation; γ-knife
前言:在肿瘤治疗方面,手术治疗、化学药物治疗和放射性治疗并列成为三种主要的治疗手段。放射治疗已经成为肿瘤必不可少的治疗手段之一。到目前为止,癌症的治愈率已经超过50%,其中放射治疗方法参与的病人在世界上,大约是60%,在中国达到70%左右。完全由放射线治愈的癌症病人大约在世界上已经达到25%[1]。为了在尽可能保护正常组织的情况下消灭肿瘤细胞,提高治疗肿瘤时对正常组织的保护,提高在肿瘤组织和正常组织中的剂量比(T/N比)是放疗追求的目标。多源立体定位的伽玛同位素放疗装置(伽玛刀)就是用于达到这个目的而设计的同位素治疗装置,是“钴炮”等这类治疗装置的发展。
, 百拇医药
在进行放射治疗剂量学研究应该包括两个方面和三种手段。两个方面是指宏观剂量和微观剂量的问题;三种手段是指解析方法计算、Monte Carlo (MC) 计算和实验测量。由于计算速度的问题,临床上使用的剂量计算方法是近似的解析计算方法,这种计算方法速度快,但是准确性差,必须加上各种修正,这些修正量是通过MC计算得到的,为了准确起见,MC计算需要尽可能好的实验验证,至少在相对计算的基础上,测量若干个实验值作为绝对定标。
近几年来, 国内伽玛刀技术和临床应用发展得很快,临床上使用的伽玛刀已达13台之多,而且还有增加的趋势。目前世界上伽玛刀的剂量计算大多采用Leksell gamma unit的Kula治疗计划系统[2]中的剂量计算方法。其剂量计算采用单源效果累加的方法实现。在靶点处,该方法把靶物质分成若干个小体积元,小体积元的总数为33×33×33个,其边长根据肿瘤的大小进行调整。其剂量计算是按均匀介质模型进行的。实际上这个方法有改进和进一步研究的必要。 本文介绍了用MCNP3.0a的早期版本进行MC模拟计算的结果。我们计算了在单源情况下和多源情况下的等位剂量分布曲线,及其剂量计算中粒子能量的展宽函数。目前的计算结果用Leksell Gamma Unit在相同条件下提供的数据相同(有意识的比较),以此为基础,进行了别的剂量学方面的模拟计算。这些工作为我们深入开展放疗剂量学研究和微机编程打下了基础。
, http://www.100md.com
1 原理和方法
现有的伽玛刀用的同位素是60Co放射源,其能量比较单一,在Monte Carlo计算时,对源分布的模拟是比较容易的。主要的改进,是要增加一个对治疗系统几何结构模拟的程序, 这个程序是我们自己编写的。在计算中,光子和物质相互作用过程中主要考虑了相干散射、非相干散射、光电效应、电子对效应。实际上,由于伽玛能量比较低,电子对效应基本可以忽略。相干散射发生在低能端,主要是模拟光子在介质中改变方向的飞行,光子在靶物质中没有能量沉积;非相干散射中产生的电子,无论能量多大,都作就地能量沉积处理;发生光电效应时考虑了荧光发射和内转换电子;发生电子对效应时,产生正负电子,其动能就地积沉,正负电子湮灭产生的2个伽玛光子,在模拟中被继续跟踪。通过以上机制计算在脑肿瘤周围的能量沉积,经计算转换成吸收剂量[3]。
2 对单源的模拟
在使用剂量叠加方法时,对单个60Co放射源的模拟是整个剂量计算的核心问题。模拟时,假定伽玛光子从Z轴正方向垂直入射,几何块为长和宽都为16cm有一定厚度的长方体,剂量计算Z方向的步长为1mm,几何块1为靶点位置,点源S到靶点位置的距离为40.1cm,皮肤表面到靶点的距离为5.0cm。几何块51为空气隔层,几何块1~50的靶物质填充为脑组织。
, 百拇医药
在空气隔层的上方为一个带锥形准直器的铅屏蔽体,其准直孔径同Leksell Gamma Unit相同。以靶点为中心,大小为1mm×1mm×1mm的体积元,共40×40个;从皮肤到肿瘤的位置,沿z方向也分成1mm×1mm×1mm的体积元,共40×50个。按此简化模型,我们分别模拟了18mm、14mm、8mm、4mm四种准直孔径的结果。以8mm孔径为例的计算几何结构如图1的单源几何模型所示,其模拟的计算结果示于图2。

图1 单源几何结构示意图。

图2 8mm孔径的等剂量曲线(a: x-y平面;b: x-z平面)
图2a中的等剂量曲线以中心的剂量为最大,由内向外的剂量从90%逐步递减到10%。图2b的等剂量曲线由上向下从90%逐步递减到50%。我们定义伽玛刀的锐度作为剂量在肿瘤和正常组织分界处变化速度快慢的物理量。它表示组织中的吸收剂量从90%降到10%时的空间距离。由上图2a可见,8mm准直器在单源情况下的锐度为1.5mm。
, 百拇医药
3 多源情况下的模拟
由于Leksell伽玛刀共有201个放射源,分布在5个环带上,各个环带上有44、44、40、38、35个准直器,如图3a所示。头部模型采用椭球形,如图3b,三层椭球由外向内填充皮肤、骨胳、脑组织等成份。靶点位置选在距椭球中心4.5cm处,距皮肤表面5cm处。

图3 a放射源和准直器模型,b头部模型(注:图3a中只画出了五个环带中两个)
根据上述模型,模拟结果如图4。

图4 8mm孔径的等剂量曲线(a: x-y平面;b: x-z平面)
, http://www.100md.com 图4中等剂量曲线中的等剂量曲线的剂量从中心点开始由内向外从90%降到10%。由上图可知,其锐度比单源情况大,为7.3mm,这是因为各路伽玛光子交叉处形成的半影,使得剂量分布的锐度减低。计算结果还表明,半剂量曲线的宽度在x、y、z三个轴上分别为11.3、11.3、9.3,同文献[1]中给出的实验数据大体相同。我们按照同样方法还计算了4mm,14mm,188mm准直器的剂量分布,其半剂量曲线的宽度分别为6.0mm,19.5mm,25.0mm。相应的锐度分别为3.5mm,12.0mm,和12.1mm。
基金项目:北京自然科学基金和国家教育部黄斐增回国人员基金资助项目
参考文献:
[1] Advances in Hydrotherapy, Edited by Ugo Amaidi et al., Press. Elsevier 1997.
[2] User's manual of Leksell Gamma Unit,Elekta Edition, April 1992.
[3] Kindl, et al. Z. Med. Phys.4(1994)215-219.
[4] 郭景新.伽玛刀剂量的Monte Carlo 模拟[D]. 1998.
收稿日期:1998-12-14, http://www.100md.com