下体负压暴露时心血管系统反应的计算机模拟研究
作者:郝卫亚 吴兴裕 张立藩 冯林华 孙喜庆 姚永杰
单位:第四军医大学空军医学系,西安 710032
关键词:数学模型;心血管系统;下体负压;计算机模拟
航天医学与医学工程990407摘要:目的 仿真研究心血管系统对下体负压(LBNP)的反应。方法 建立了一个数学模型,模型包括7部分:血液重分配控制、左室灌注、左室、外周循环、心率调节控制、外周阻力调节控制、静脉紧张程度控制。其中,心率和静脉紧张度受动脉压力感受器反射控制,而外周阻力则同时受动脉压力感受器和心肺压力感受器的反射控制。结果 利用所建模型,模拟了0~-10.64 kPa(-80 mmHg)范围内LBNP暴露时心血管系统的反应,模拟LBNP暴露时收缩压、平均压、心率和心输出量的变化以及血压反应过程,仿真结果均与人体实验结果吻合。结论 所建模型是有效的,可以模拟LBNP下血液动力学的短期反应。
中图分类号:R852.22,TP391.9 文献标识码:A 文章编号:1002-0837(1999)04-0262-05
Computer Simulation of Cardiovascular Response to Lower Body Negative Pressure
HAO Wei-ya, WU Xing-yu, ZHANG Li-fan, FENG Lin-hua,SUN Xi-qing, YAO Yong-jie
Abstract: Objective To simulate the cardiovascular response to lower body negative pressure (LBNP). Method A computer model was developed.It had 7 subparts: the redistribution of blood, the filling of left ventricle, left ventricle, peripheral circulation, control of heart rate, control of peripheral resistance and control of venous tone. The heart rate and venous tone were controlled by high-pressure receptor baroreflex, while the peripheral resistance was controlled by high- and low-pressure receptor baroreflexes. Result With the help of the model,cardiovascular response to LBNP up to -10.64 kPa(-80 mmHg)were simulated, including the changes of systolic blood pressure, mean blood pressure, heart rate and cardiac output.The time-dependent response to a LBNP profile was also simulated. The simulation results coincided well with human experiments. Conclusion The model is valid and can accurately reproduce the short-term hemodynamic response to LBNP.
Key words:mathematical model;cardiovascular system;lower body negative pressure;computerized simulation
Address reprint requests:HAO Wei-ya.Department of Aerospace Medicine,The Fourth Military Medical University,Xi'an 710032,China
在航空航天医学中,下体负压(LBNP)是评价人体在卧床和失重后心血管脱锻炼程度和对抗立位耐力下降的常用技术手段[1,2],它不受重力因素和下肢肌肉收缩的限制。LBNP的生理反应是:提高心率(HR)和下体血液的积聚量,降低系统血压(BP)和平均血压(MAP);同时,脉压差和心输出量(CO)也降低。心血管系统对LBNP反应十分复杂,涉及很多的生理机制,包括不同部位血管床的静脉顺应性,心脏的Starling定律和压力反射等。目前认为,这些机制中一些小的变化都会引起立位耐力的降低[1]。很难通过人体或动物实验估计这些因素在立位耐力降低中的单独作用。一种变通的办法是建立一个可以模拟人体立位应激反应的数学模型。适当地改变模型中的相应参数,分析结果,就可以帮助我们了解各个生理因素的变化在立位反应中的作用。因此,建立可以模拟LBNP时心血管系统反应的数学模型显得十分重要。
本工作以Melchior模型[3]为基础,建立了一个用来模拟人体LBNP时心血管系统反应的数学模型,并以一定的人体试验加以验证。
方 法
模型的建立
生理学基础 心血管系统对立位应激的反应遵循一系列生理过程:血液的再分配—下体血管外负压增加了血管跨壁压,导致血液的重新分配,进而中心静脉压(CVP)降低;左室灌注—CVP的降低使得左室的灌注降低,导致左室舒张期末的容积降低;心脏与外周循环的耦合—左室舒张期末容积的降低导致每搏输出量(SV)和动脉压的降低;压力反射的代偿—动脉和心肺压力反射通过提高心率,增加系统阻力(SVR)和降低静脉顺应性代偿血压的降低。
模型简介 基于以上四个生理机制,并以Melchior模型[3]为基础,我们建立了适于模拟立位应激反应的心血管系统数学模型。模型包括以下7部分:血液重分配控制、左室灌注、左室、外周循环、心率调节控制、外周阻力调节控制、静脉紧张程度控制(图1)。与Melchior模型相比,本模型在以下几个方面有所改进。
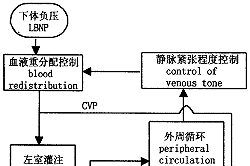
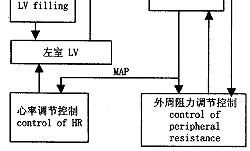
图1 人体心血管系统模型框图
Fig.1 Block diagram of human cardiovascular simulation model
细化人体静脉系统 在血液重新分布系统中,按照人体解剖特点,把人体静脉系统适当地细化,并考虑了静脉在跨壁压为负值时可能发生塌陷的生理现象。静脉系统的顺应性大约是动脉系统的24倍[4],在立位应激时,动脉系统在血液重新分布中的作用微不足道。在微循环中,管内压力变化时几乎看不到管径随之变化,象是刚性管[5]。再加上血液主要分布在静脉系统中,因此,在人体受到立位应激时,血液的转移主要发生在静脉系统中。我们假设血液的重新分布仅限于静脉之中,把静脉系统按照解剖结构划分为7个组分,分别代表头部和上肢部(HUL)、胸部(THO)、腹部(ABD)、臀部和骨盆部(PB)、大腿(THI)、小腿(CAL)及足部(FT)(图2)。LBNP暴露时,臀部和骨盆、大腿、小腿及足部处于负压之中。由于LBNP只部分地传递到静脉的周围组织[3],则静脉周围组织的负压为Ktrans.LBNP,其中Ktrans为传递系数。假设LBNP暴露时,静脉内血压各处相同,均为CVP,则在LBNP暴露时,臀部和骨盆、大腿、小腿及足部静脉的跨壁压为:
Ptrans=CVP-Ktrans×LBNP(1)
而头部和上肢、胸部、腹部静脉的跨壁压为:
Ptrans=CVP(2)
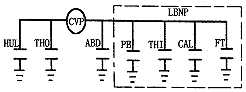
图2 血液重新分配模型
Fig.2 Model of blood redistribution
LBNP暴露时血液重新分布不仅与血管跨壁压有关,而且与各组分的顺应性有关。由于LBNP变化较大,有必要考虑血管顺应性的非线性。我们用公式(3-1、3-2)拟合各组分的血容量变化量ΔV与跨壁压ΔPtrans之间的非线性关系。其中:ΔVm+是该组分静脉的最大血容量增量,ΔVm-表示静脉在ΔPtrans为负值时最大血容量减少量。式(3-2)表示静脉在跨壁压为负值时的塌陷过程。根据方程(1~3)并假设血液的总量不变,可求出LBNP暴露时的ΔCVP。
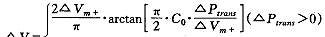 (3-1)
(3-1)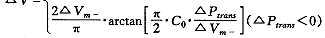 (3-2)
(3-2)引入静脉紧张度变化的反射机制 LBNP暴露致血压降低后,静脉紧张度提高,促进外周静脉系统中的血液回流,使CVP有所回升。采用Green和Miller的血管弹性控制模型[6]:
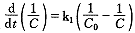 -k2[p(t-λ)-p0](4)
-k2[p(t-λ)-p0](4)控制不同部位静脉紧张度变化。式中C0和p0分别是稳态时的顺应性和MAP,λ为一时间延迟常数,k1和k2为变化率系数。
提出一个新的压力反射模型并应用于模型之中 系统阻力和心率受到动脉压力和心肺压力感受器引起的反射调节作用。在LBNP暴露时,感受器受到的压力刺激发生变化,它们把这些变化以电信号形式传入CNS,CNS综合调制这些信号,并调节血管阻力和心率来维持系统血压的稳定。这个过程需要一定的时间d,因此压力反射活动存在着时间延迟。不仅如此,它还有记忆效应。如果忽略其它因素的影响,某一时刻t的阻力或心率不仅与(t-d)时刻的血压P(t-d)有关,而且与(t-d)时刻以前的所有血压有关。基于这个观点,我们用带有时间延迟的遗传积分来计算某一时刻的血压变化的刺激水平,它是所有以前时间刺激的总和,具体用积分关系式表示:
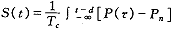 .e-(t-d-τ)/Tcdτ(5)
.e-(t-d-τ)/Tcdτ(5)式中τ是时间积分变量,P(τ)是感受器受到的血压随时间变化函数[对于动脉压力感受器,P(τ)为MAP,对于心肺压力感受器则为CVP],Pn是正常压力值(即人体安静仰卧时MAP或CVP),Tc是常数。心率受动脉压力感受器控制,心率的控制方程(6)中,HRmin和HRmax分别是心率的阈值和饱和值,S0是常数。
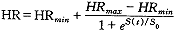 (6)
(6)外周阻力有5部分:心脑阻力,由于自动调节作用,其阻力随血压变化,使心脑血流量保持不变;腹部阻力;肾阻力;下肢阻力;上肢阻力。腹部、肾和下肢阻力受到动脉压力感受器反射的调节作用,而上肢阻力受到心肺压力反射的调节作用,其控制函数与心率控制函数类似。
经上述改进,模拟LBNP的暴露范围由Melchior模型的0~-5.32kPa扩展到-10.64kPa;而且,由于反射控制模型中引入了时间延迟和新的压力反射控制函数,模型成为时间依赖性模型,可以仿真下体负压时心血管系统在中枢系统控制下的代偿作用过程。
系统的正常状态 血压为15.54/10.13kPa,心率为72次/min,左室舒张期末容积为145ml,每搏输出量约为82ml,中心静脉压约为0.798kPa。
人体LBNP试验
步骤 被试者为6名健康青年男性,年龄23.8±6.1岁,身高165.8±7.5cm,体重54.3±7.88kg。试验采用仰卧位LBNP。步骤为:被试者仰卧休息5min,记录其基础血压和心率;然后,在10s内负压裤降低到暴露值,持续3min。记录1min、2min和3min时的血压和心率。暴露3min后解除负压,休息5min后再进行下一负压值的试验,依次为-4.00kPa、-6.67kPa及-9.33kPa。
数据处理 1名在-6.67kPa、2min时出现晕厥前症状,停止了实验,未统计其数据。每名被试者在不同LBNP值暴露下,心率、收缩压和平均压(舒张压+脉压/3)的变化量由其负压暴露时三次测量结果的平均值与负压暴露前的基础值相减而得。再平均5名被试者在不同LBNP值暴露下心率、收缩压和平均压的变化量。计算结果以
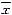 ±s表示。
±s表示。模拟LBNP试验 系统启动以后,对其作用一定的LBNP值,由血液重新分配控制系统计算出中心静脉压的变化(CVP),继而计算出LBNP后的左室收缩期末容积(LVEDV),然后,左室与外周循环发生耦合作用,计算出每个心动周期的BP随时间变化,同时也可计算出其它主要的血液动力学变量,包括:SBP,MAP,HR,CVP,SV,CO,LVEDV和SVR。一个心动周期完成后,根据新的动静脉血压,通过压力反射控制调节下一周期的HR、SVR、静脉紧张程度,并在下个周期开始前,根据调节后的静脉紧张程度的变化,重新调节血液的分布,计算CVP,再开始下个周期的运行。这样循环往复,直至系统达到新的稳定状态(平均动脉压与上一周期的差值小于0.133kPa)后,解除LBNP。
结 果
人体试验与模拟LBNP实验结果
表1是我们的人体试验和模型模拟试验的结果。可以看出,模拟结果与实验结果符合较好。图3是模型模拟下体负压时心血管系统主要血液动力学变量的变化,其中,SBP,MAP和HR分别用LBNP暴露时与基础值的差值表示,而CO则用LBNP暴露时它们相对于基础值的百分比表示。图中还显示了我们的以及文献报道的人体试验结果以作对照[2,7,8]。其中,Blomqvist的数据是综合大量人体试验数据的结果。可以看出,本研究模拟实验所得的血流动力学变量无论从定性还是定量来看,均与人体试验结果吻合较好。
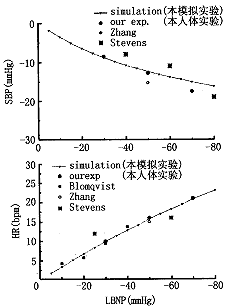

图3 不同LBNP暴露时收缩压、平均压、心率和心输出量的变化
Fig.3 Changes of systolic pressure,mean arterial blood pressure,heart rate,and cardiac output during LBNP
表1 人体试验及计算机模拟下体负压实验心率和血压的结果对照
Table 1 Changes of heart rate and blood pressure by computer simulation vs human-test during LBNP LBNP
(kPa)
心率变化(HR change)(bpm)
收缩压变化(SBP change)(kPa)
平均压变化(MAP change)(kPa)
人体试验
(human-test)
模拟试验
(simulation)
人体试验
(human-test)
模拟试验
(simulation)
人体试验
(human-test)
模拟试验
(simulation)
-4.00
8.27±3.55**
10
-1.14±0.97*
-1.07
-0.54±0.42*
-0.41
-6.67
15.19±4.15**
16
-1.70±0.75**
-1.65
-0.67±0.53*
-0.63
-9.33
26.67±10.16**
21
-2.33±0.23**
-2.01
-0.75±0.41**
-0.81
注:*P<0.05,**P<0.01,与LBNP前相比,人体实验的基础值(n=5):HR,68.87±10.93 bpm;SBP,15.97±1.48 kPa;MAP,11.46±0.87 kPa.模拟实验的基础值:HR,74 bpm;SBP, 15.56 kPa;MAP, 12.64 kPa
Note:*P<0.05,**P<0.01,as compared wtih pre-LBNP,basic values in human test (n=5):HR,68.87±10.93 bpm;SBP,15.97±1.48 kPa;MAP,11.46±0.87 kPa,basic values in simulation study:HR,74 bpm;SBP, 15.56 kPa;MAP, 12.64 kPa 模拟LBNP暴露时系统反应过程
图4是模拟LBNP为-6.67kPa暴露时系统血压随时间的变化。可以看出,血压随着LBNP暴露值的增加逐渐降低,在达到-6.67kPa时,血压处于最低点;之后,由于生理代偿作用(HR、SVR和静脉紧张程度的增加),使得血压有所提高,并于LBNP暴露约15s时达峰值;但是,系统不能维持这种状态,血压很快降到一个新的稳定的“理想值”;在LBNP暴露解除时,由于这时的HR,SVR和静脉紧张程度都处于较高的应激状态,血压有一过性的增高现象,之后,血压迅速调节到正常水平。整个LBNP暴露过程中血压的变化与文献报道相同[7,8]。LBNP暴露时,SBP降低较多,而DBP较暴露前略有升高;脉压差在LBNP暴露时降低,与有关报道相符[7]。
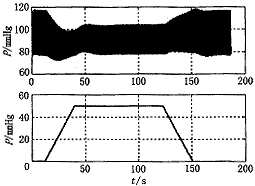
图4 -6 .65 kPa(-50 mmHg)LBNP暴露时血压变化的模拟结果
Fig.4 Simulated changes of blood pressure during -6.65 kPa(-50 mmHg) LBNP
讨 论
我们建立的模型虽是以Melchior[3]模型为基础,但在分段、压力反射机制等方面作了较大的改进,所建立的模型既不象多组分(或多节段)那么繁琐,又不至于过分简单而无法获得重要的血流动力学变量;模型中对系统的分段比较简化,而对人体系统在LBNP下的调节反应考虑比较详细且符合生理特点。Stevens等[5]指出,LBNP解除后,所有的生理量在3min后即回到基础值,在解除后的前10~15 s内收缩压和脉压超过正常值,之后又迅速降低到正常值,这与本工作计算机模拟实验结果十分吻合。本工作中人体LBNP实验是暴露3min,然后休息5min,可以认为LBNP暴露下的系统反应是一种短期反应,即系统调节反应中没有内分泌系统参与,系统内的体液保持不变;因此,在模型中没有考虑人体在LBNP时体液调节作用。
一个数学模型,不可能只采用一套参数而其模拟结果符合所有的人体实验结果,因为这些结果是从不同研究中获得的,它们除了个别实验条件可能相同(如卧位休息状态)外,其他因素可能都不相同(如被试者从不同的人群而来)。但是,如果数学模型的结构正确,也就是说模型中植入了被研究现象的基本机制,那么模拟结果总是朝正确的方向发展。基于这些观点,我们认为,本模型采用的LBNP作用机制符合实际,故对LBNP暴露时心血管系统反应机理的研究具有一定的意义。
参考文献
[1]Watenpaugh DE,Hargens AR. The cardiovascular system in microgravity[M]. In: Fregly MJ and Blatteis.CM eds.Handbook of Physiology: Environmental Physiology. Ⅲ: The Gravitational Environment,1: Microgravity. New York: Oxford University Press, 1996: 631~674
[2]Blomqvist CG,and Stone HL. Cardiovascular adjustment to gravitation stress[M]. In: Handbook of Physiology. The Cardiovascular System Peripheral circulation and Organ Blood Flow. sect.2,vol.Ⅲ ,pt. 2 ,Bethesda.MD:Am Physiol Soc,1983:1025~1063
[3]Melchior FM,Srinivasan RS, Thullier PH et al. Simulation of cardiovascular response to lower body negative pressure from 0 to -40 mmHg[J]. J Appl Physiol,1994,77(2):630~640
[4]Guyton AC, Arstrong GG, Chipley PL. Pressure~volume curves of the arterial and venous systems in the living dogs[J]. Am J Physiol,1956,184:253~258
[5]陈君楷.心血管血流动力学[M].成都:四川教育出版社,1990:397~402
[6]Green JF, Miller NC. A model describing the response of the circulatory system to acceleration stress[J].Annals of Biomedical Engineering, 1973,1(3):455~467
[7]张立藩,郑军,王兴邦,等.六个月有氧锻炼对立位耐力及循环反应的影响[J].中华航空航天医学杂志,1997,8(4):203~207
[8]Stevens PM, and Lamb LE. Effects of lower body negative pressure on the cardiovascular system[J].Am J Cardiol, 1965,16:506~515
收稿日期:1998-08-11
|
微信文章
关注百拇
评论几句
搜索更多
|

