人耳内声音传递的统计规律
作者：陈洪财
单位：佳木斯大学，佳木斯154007
关键词：打击脉冲；功率传递函数；传递因子
黑龙江医药科学000303 提要 从物理学的基本原理出发，结合耳膜的特殊结构和振动模式，得出打击脉冲，并比较麦克斯-玻尔兹曼的统计理论，得出声音在人耳内部出现传递因子S(w )；在超声区，S(w )出现截止频率w c，在次声区，打击脉冲不连续，出现临界频率fc(fc=20Hz)[1]。
Statistical rule of sound transmission in man's ear
Cheng Hongcai
, http://www.100md.com
Abstract Based on the principle of physics, and combining with the special structure and vibration of the ear-drum, we get a impact pulse. By comparing with " Theory of Maxwell-Boltzmann", we get a transmission factor S(w ).Which within ultrasonic rauge presents cutoff frequency w o, and in the infrasonics, the impact pulse discontinues and the critical frequency fc appears.(fc=20Hz).These results also agree with the boundations of "Fletcher-Muuson" and "Robinson-Dadson" equal loudness curves.
, 百拇医药
Key words impact pulse; power transmission function; transmission factor
耳听到各种声音实际上是各种音频以空气为媒质的机械振动引起鼓膜振动的结果。当一束声波进入人耳；在中耳内部，有些人用匹配高低阻抗变压器的耦合方法，以说明声音在人耳内的传递问题。实际上，人的耳膜是一个边缘固定的振动薄膜，由于耳膜振动，没有静止驻定的稳态，入射声波在耳膜上所引起的反射波，不可能存在稳态，因此由干涉而产生的驻波不可能出现。入射声波由耳膜的振动形式直接传入内耳，用不严密的高低阻抗匹配变压器模型来说明声的传递，这种模型，不可能得出传递模式与贝塞尔函数有关，从而需要作以相关的修补更正。
1 人耳的特殊结构与声振动理论分析
1.1 人耳的仿真模型
人耳的内部结构如图1所示。人的耳膜实际上形如一椭圆(长轴≈10mm，短轴≈8.5mm)位于外耳道的尾端，它的功能是封闭和保护内耳，外听道的声振动引起耳膜振动，形成声讯息(图2)，这声讯息通过耳膜的附件-锤骨M(23mg)→砧骨I(27mg)→镫骨S(2.5mg)，
, 百拇医药
图1耳剖面的示意图
图2锤骨M的打击脉冲作用
最后传到听觉神经，在耳膜上有许多相同弹性的浮肋，呈现轴向的、同心圆分布，当微小刺激作用在耳膜上，将出现一些圆圈，可以认为圆圈的出现，随弹性张力T而变，与耳膜片的质量无关，耳膜的边缘固定在耳壳骨上。耳膜的厚度很小(≈100μm)，这意味着耳膜是一绷紧的和带有附加质量锤骨的圆膜，锤骨像锤头一样运动，打击砧骨，使锤骨的振动动能传递到内耳。耳膜两侧的空气，在声压突然变化时起着自控和缓冲作用，它不影响振动频率。
1.2 耳膜物理模型的建立
当耳膜受到外界声压P=PAejωt时，它形成受迫振动。在图3中选取中心O为极坐标原点，附加质量位于b点，中间距离ob是d，当耳膜片振动时，附加质量在惯性力作用下，随膜片振动，最终这惯性力集中作用在耳膜片上，由膜片的固定边界承受。令S为耳膜片的周界长，h b为附加质量的位移，T为弹性张力，从动力学出发可得一个二维偏微方程
(1)
, 百拇医药
式中采用的是常用的符号。
图3人耳膜的振动模型
因为耳膜的尺寸很小，声压在耳膜上可以认为是均匀分布的，它在极角间的差异很小，即
方程(1)可简化为一维微分方程
(2)
这是对膜片任意一点都适用的方程。如选取附加质量的落点b为研究点，得出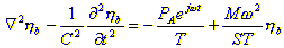
(3)
这是附加质量位移的一维偏微方程。
, http://www.100md.com
1.3 附加质量在耳膜上的受迫振动分析
方程(3)中，如附加质量M=0，且膜的边缘固定，可得出方程组
其解是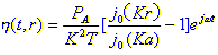
(4)
式中，
是对应于无载膜的参数，C是膜在半径方向振动的传速，在均匀膜中C是一恒量，J0(Kr),J0(Ka)是零级贝塞尔函数。带有附加质量时，重新研究方程(2)，可将其变成
(5)
, 百拇医药 式中，ηb仍是(t,r)的函数。把h b(t,r)=R(r)ejwt代入式(5)，得当边缘固定时，式(5)的解为
(6)
以及
(7)
当M=0时，可以得出K’=K，与无附加质量时的情形符合，也证明了K’是另一恒量，从式(7)可以得出附加质量M的振动速度
(8)
1.4 人耳膜的能量模型
当耳膜受外来的声压时，一部分声波能量使耳膜片作受迫振动，另一部分传递至附加质量，引起它随膜片一起振动，膜片振动是处在绷紧的张力中，它有平均动能和平均势能，膜片的总能是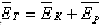
，我们可称它是保守能，不能直接传递。
, http://www.100md.com
附加质量锤骨随膜片振动，但它不受膜片绷紧的力的作用，因此它的平均能量是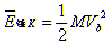
(M是附加锤骨的质量)，为了计算附加质量的平均动能，用
的实数部分表示可以得
(9)
人耳膜的能量：包括膜片的总能和附加质量的平均动能
，称为
，膜片的总能贮蓄在系统内部，附加质量的动能可由锤骨打击砧骨直接传至内耳。
2 人耳内的声传递函数
, 百拇医药 2.1 功率传递的实效函数
耳膜振动一次，传递能量
而1秒内附加质量振动打击f次，所以功率传递是
(10)
将方程(9)代入(10)得
(11)
式中a 1是一参量方程
(11)称为声功率传递函数，并指出
成正比例，如果人耳按同一比例响应，它将出现同"热辐射"一样引起高频灾难，因此必须有一修正因子。参考麦克斯韦(Maxwell)-玻尔兹曼(Boltzmann)的统计分配率[2]，修正后的实效功率函数为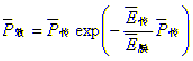
(12)
, http://www.100md.com
修正因子与人耳的结构
和功率传递函数
有关。
2.2 人耳内部的声音传递规律
方程(12)可写成
(13)
方程(13)称作为耳的实效功率传递函数的数学表达式，它是声音在人耳内部传递的统计规律，令
(14)
S(ω)称为人耳内部的传递因子，它随w 3的幂指数而衰减，这就可避免"高频灾难"的出现[3]。
, 百拇医药
3 时效功率传递函数的结论
令
(14)式可变为
当
,
这些频率是可闻的。
在超声区，没有任何讯息记录下来
因S(ω)可以展开成无穷级数
(15)
该级数是收敛的，对式(15)取近似值
, http://www.100md.com
式中，S(ω)后面的诸余项之和的影响小于最小耳闻声的功率，w c为截止频率，所以人耳接收不到高于截止频率的超声。在可闻声区，频率较高，声音振动的传播是连续的。根据哈斯(Hass)效应[4]，人耳对声音断或续的分辩本领的临界时间50ms。如果两次锤击声的中间间隔短于50ms，人耳听到锤击声是连续的；如果两个单音的中间间隔时间超过50ms人们听到孤立的打击脉冲，不是连续的声振动，对应于临界频率，得出
临界频率f临=1/t临，式中，临界时间t临≤50ms，即f≥20Hz。
参考文献
1.杜功焕.声学基础(上册).上海:上海科学出版社,1986.
2.肖尼斯基.声音.林大悃,译.北京:中国建筑工业出版社,1985
3.李世光.建筑物理.第2版,北京:中国建筑出版社,1986
4.白瑞纳克.声学.马大猷等译.北京:高等教育出版社,1959, 百拇医药
单位：佳木斯大学，佳木斯154007
关键词：打击脉冲；功率传递函数；传递因子
黑龙江医药科学000303 提要 从物理学的基本原理出发，结合耳膜的特殊结构和振动模式，得出打击脉冲，并比较麦克斯-玻尔兹曼的统计理论，得出声音在人耳内部出现传递因子S(w )；在超声区，S(w )出现截止频率w c，在次声区，打击脉冲不连续，出现临界频率fc(fc=20Hz)[1]。
Statistical rule of sound transmission in man's ear
Cheng Hongcai
, http://www.100md.com
Abstract Based on the principle of physics, and combining with the special structure and vibration of the ear-drum, we get a impact pulse. By comparing with " Theory of Maxwell-Boltzmann", we get a transmission factor S(w ).Which within ultrasonic rauge presents cutoff frequency w o, and in the infrasonics, the impact pulse discontinues and the critical frequency fc appears.(fc=20Hz).These results also agree with the boundations of "Fletcher-Muuson" and "Robinson-Dadson" equal loudness curves.
, 百拇医药
Key words impact pulse; power transmission function; transmission factor
耳听到各种声音实际上是各种音频以空气为媒质的机械振动引起鼓膜振动的结果。当一束声波进入人耳；在中耳内部，有些人用匹配高低阻抗变压器的耦合方法，以说明声音在人耳内的传递问题。实际上，人的耳膜是一个边缘固定的振动薄膜，由于耳膜振动，没有静止驻定的稳态，入射声波在耳膜上所引起的反射波，不可能存在稳态，因此由干涉而产生的驻波不可能出现。入射声波由耳膜的振动形式直接传入内耳，用不严密的高低阻抗匹配变压器模型来说明声的传递，这种模型，不可能得出传递模式与贝塞尔函数有关，从而需要作以相关的修补更正。
1 人耳的特殊结构与声振动理论分析
1.1 人耳的仿真模型
人耳的内部结构如图1所示。人的耳膜实际上形如一椭圆(长轴≈10mm，短轴≈8.5mm)位于外耳道的尾端，它的功能是封闭和保护内耳，外听道的声振动引起耳膜振动，形成声讯息(图2)，这声讯息通过耳膜的附件-锤骨M(23mg)→砧骨I(27mg)→镫骨S(2.5mg)，
, 百拇医药
图1耳剖面的示意图
图2锤骨M的打击脉冲作用
最后传到听觉神经，在耳膜上有许多相同弹性的浮肋，呈现轴向的、同心圆分布，当微小刺激作用在耳膜上，将出现一些圆圈，可以认为圆圈的出现，随弹性张力T而变，与耳膜片的质量无关，耳膜的边缘固定在耳壳骨上。耳膜的厚度很小(≈100μm)，这意味着耳膜是一绷紧的和带有附加质量锤骨的圆膜，锤骨像锤头一样运动，打击砧骨，使锤骨的振动动能传递到内耳。耳膜两侧的空气，在声压突然变化时起着自控和缓冲作用，它不影响振动频率。
1.2 耳膜物理模型的建立
当耳膜受到外界声压P=PAejωt时，它形成受迫振动。在图3中选取中心O为极坐标原点，附加质量位于b点，中间距离ob是d，当耳膜片振动时，附加质量在惯性力作用下，随膜片振动，最终这惯性力集中作用在耳膜片上，由膜片的固定边界承受。令S为耳膜片的周界长，h b为附加质量的位移，T为弹性张力，从动力学出发可得一个二维偏微方程
(1), 百拇医药
式中采用的是常用的符号。
图3人耳膜的振动模型
因为耳膜的尺寸很小，声压在耳膜上可以认为是均匀分布的，它在极角间的差异很小，即
方程(1)可简化为一维微分方程
(2)这是对膜片任意一点都适用的方程。如选取附加质量的落点b为研究点，得出
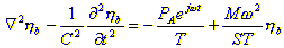(3)这是附加质量位移的一维偏微方程。
, http://www.100md.com
1.3 附加质量在耳膜上的受迫振动分析
方程(3)中，如附加质量M=0，且膜的边缘固定，可得出方程组
其解是
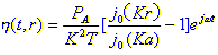(4)式中，
是对应于无载膜的参数，C是膜在半径方向振动的传速，在均匀膜中C是一恒量，J0(Kr),J0(Ka)是零级贝塞尔函数。带有附加质量时，重新研究方程(2)，可将其变成 (5), 百拇医药 式中，ηb仍是(t,r)的函数。把h b(t,r)=R(r)ejwt代入式(5)，得当边缘固定时，式(5)的解为
(6)以及
(7)当M=0时，可以得出K’=K，与无附加质量时的情形符合，也证明了K’是另一恒量，从式(7)可以得出附加质量M的振动速度
(8)1.4 人耳膜的能量模型
当耳膜受外来的声压时，一部分声波能量使耳膜片作受迫振动，另一部分传递至附加质量，引起它随膜片一起振动，膜片振动是处在绷紧的张力中，它有平均动能和平均势能，膜片的总能是
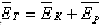，我们可称它是保守能，不能直接传递。, http://www.100md.com
附加质量锤骨随膜片振动，但它不受膜片绷紧的力的作用，因此它的平均能量是
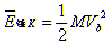(M是附加锤骨的质量)，为了计算附加质量的平均动能，用的实数部分表示可以得 (9)人耳膜的能量：包括膜片的总能和附加质量的平均动能
，称为，膜片的总能贮蓄在系统内部，附加质量的动能可由锤骨打击砧骨直接传至内耳。2 人耳内的声传递函数
, 百拇医药 2.1 功率传递的实效函数
耳膜振动一次，传递能量
而1秒内附加质量振动打击f次，所以功率传递是 (10)将方程(9)代入(10)得
(11)式中a 1是一参量方程
(11)称为声功率传递函数，并指出
成正比例，如果人耳按同一比例响应，它将出现同"热辐射"一样引起高频灾难，因此必须有一修正因子。参考麦克斯韦(Maxwell)-玻尔兹曼(Boltzmann)的统计分配率[2]，修正后的实效功率函数为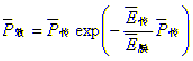 (12), http://www.100md.com
修正因子与人耳的结构
和功率传递函数有关。2.2 人耳内部的声音传递规律
方程(12)可写成
(13)方程(13)称作为耳的实效功率传递函数的数学表达式，它是声音在人耳内部传递的统计规律，令
(14)S(ω)称为人耳内部的传递因子，它随w 3的幂指数而衰减，这就可避免"高频灾难"的出现[3]。
, 百拇医药
3 时效功率传递函数的结论
令
(14)式可变为当
,这些频率是可闻的。在超声区，没有任何讯息记录下来
因S(ω)可以展开成无穷级数
(15)该级数是收敛的，对式(15)取近似值
, http://www.100md.com
式中，S(ω)后面的诸余项之和的影响小于最小耳闻声的功率，w c为截止频率，所以人耳接收不到高于截止频率的超声。在可闻声区，频率较高，声音振动的传播是连续的。根据哈斯(Hass)效应[4]，人耳对声音断或续的分辩本领的临界时间50ms。如果两次锤击声的中间间隔短于50ms，人耳听到锤击声是连续的；如果两个单音的中间间隔时间超过50ms人们听到孤立的打击脉冲，不是连续的声振动，对应于临界频率，得出
临界频率f临=1/t临，式中，临界时间t临≤50ms，即f≥20Hz。
参考文献
1.杜功焕.声学基础(上册).上海:上海科学出版社,1986.
2.肖尼斯基.声音.林大悃,译.北京:中国建筑工业出版社,1985
3.李世光.建筑物理.第2版,北京:中国建筑出版社,1986
4.白瑞纳克.声学.马大猷等译.北京:高等教育出版社,1959, 百拇医药