一种抑制心电信号50 Hz工频干扰的改进Levkov方法
作者:孙京霞 白延强 杨玉星
单位:孙京霞 白延强(航天医学工程研究所,北京 100094);杨玉星(华中理工大学,湖北 430074)
关键词:心电信号;模板;工频干扰;滤波
航天医学与医学工程000310摘要: 目的 探讨一种用于抑制心电信号中50 Hz工频干扰的新方法。 方法 在Levkov滤波法的基础上加入QRS开关函数,并用此法与几种常用的滤波方法进行比较。 结果 该方法算法简单,处理速度快,对强、弱噪声滤波效果都较好。 结论 该方法对于抑制心电信号中50 Hz工频干扰有很好的应用前景。
中图分类号:R540.41 文献标识码:A
文章编号:1002-0837(2000)03-0196-04
, http://www.100md.com
An Improved Levkov Method for Filtering 50 Hz Interference in ECG Signals
SUN Jing-xia,BAI Yan-qiang,YANG Yu-xing
Abstract: Objective To find a new method for repressing the 50 Hz power-line interference in ECG signals. Method An improved method based on Levkov filtering method and inserted QRS switch function, several ordinary methods were compared with it. Result This method had a simple algorithm, fast processing speed and good result of filtering both strong and weak interference. Conclusion This method provides a good base for further disposing.
, 百拇医药
Key words:ECG signals;templet;power-line interference;filtration
在采集ECG信号过程中,常常受到各种干扰,其中50 Hz工频干扰是最主要的一种。如何有效抑制50 Hz工频干扰,是处理心电信号的首要任务。目前比较常用的方法有:平滑滤波,中心频率固定的带阻滤波,自适应滤波,Levkov滤波等。
1984年,Levkov首先提出对ECG信号的线性段和非线性段采用不同处理方式的数字滤波法[1]。1988年Christov改进该算法[2],引入ECG信号的线性段判据M来加快滤波的速度。在线性段判断过程中,M的选择非常关键,M取值较小,滤波效果差,M取值较大,滤波效果好,但削峰严重。对此,我们引入QRS波开关控制的方法,即在Levkov基础上,加入QRS识别的开关函数法。此法既比较好地实现滤波,又保持波形不失真。经实际检验,该方法滤波效果好,对于抑制心电信号中50 Hz工频干扰有很好的应用前景。
, http://www.100md.com
几种常用的滤波法
下面介绍的几种滤波都是在采样频率为200 Hz,工频干扰为50 Hz的条件下实现的。
平滑滤波 平滑滤波是数字滤波方法中较早被人们采用的方法[3],该方法算法简单,处理速度快,滤波效果较好,但也存在明显不足,通频带较窄,影响有用信号的分析。滤波效果如图1所示。
图1 平滑滤波示意图
Fig.1 Smooth filtering method
A:first ECG signal;B:after filtering ECG signal;C:elimination interference
, 百拇医药
其传递函数为:
差分方程为: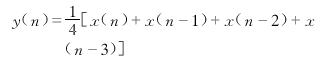
NOTCH滤波 NOTCH滤波器,又称简单整系数带阻滤波器,其原理为用一个全通网络减去一个具有相同传输延迟和增益的窄带线形相位FIR滤波器的输出,得到一个具有尖锐陷波特性的陷波滤波器[4,5]。
NOTCH滤波器传递函数为:
H(z)=z-148-(1+z-100-z-200-z-300)/[100。(1-z-4)]
, http://www.100md.com
差分方程为:y(n)=y1(n)-y2(n)/100
其中:y1(n)=x(n-148)
y2(n)=x(n)+x(n-100)-x(n-
200)-x(n-300)+y(n-4)
y1(n)为全通网络输出,y2(n)为窄带带通滤波器输出,y(n)为NOTCH滤波器输出。滤波效果如图2所示。
图2 NOTCH滤波法
Fig.2 Notch filtering method
, http://www.100md.com
自适应滤波 设原始输入x(n)为信号与噪声w(n)之和:x(n)=s(n)+w(n)
滤波后输出为y(n)。
其中e(n)为误差,d(n)为预期信号,h(n)为FIR各阶系数,N为FIR的阶数,M为数据长度。d应该随着信号变化不断调整,使E[e2]最小[6,7]。滤波效果如图3所示。
图3 自适应滤波法
Fig.3 Self-adapting filtering method
新的Levkov滤波
, http://www.100md.com
1984年,Levkov首先提出对ECG信号的线性段和非线性段采用不同处理方式的数字滤波方法。1988年Christov对该算法改进,引入ECG信号的线性段判据M来加快滤波的速度。用该方法滤波,它要求原始ECG信号满足以下两个条件:(1)采样频率fs应是工频干扰的整数倍;(2)在一个工频干扰周期T内,工频干扰采样点的幅值的代数和为0。在滤波过程中首先要识别出一个线性段,该线性段滤波后的值为这个线性段原始数据的平均值。同时求出工频干扰的值作为非线性段的工频干扰的模板。而在非线性段,其真值是用原始数据减去在临近线性段求得的干扰模板值。
Levkov滤波原理 设原始信号为Si,干扰信号为Ni,包含噪声的信号为Xi=Si+Ni, i=0,1,2,…, S0,S1,S2,S3为线性段信号,对于200 Hz采样率,相邻间距为5 ms,故:
S4-S3=S3-S2=S2-S1=S1-S0=d;
, 百拇医药
N0+N1+N2+N3=0;N0=N4;d为线性段上相邻点间的差值。
X0+X1+X2+X3
=S0+S1+S2+S3+N0+N1+N2+N3
=S1-d+S1+S1+d+S1+2d=4S1+2d
X4-X0=S4+N4-S0-N0=4d;
, http://www.100md.com
所以,T1时刻,信号和噪声分别是:
S1=[(X0+X1+X2+X3)-(X4-X0)/2]/4;
N1=X1-S1;
对于线性段可按上述模式处理。当出现非线性段时,考虑到工频干扰的相位在短时间内不会有过大的变化,可用最近计算出的与当前点同相位处的噪声作为当前噪声的预测值,则当前的信号值为: S1=X1-N1; 我们用上述改进的Levkov法(即Christov法)进行滤波,实验中发现,对于有些心电波形,滤波效果不好。分析其原因是:在该算法中引入M用来判定线性段和非线性段的指标,是滤波方法中的关键因素。Christov在fs= 400 Hz,工频干扰f=50 Hz情况下经过大量(大于200次)实验,认为M=12.0 是较为理想的值。而我们发现对于噪声较大的ECG波形,该方法滤波效果不好,这与M取值有关。M值越小,滤波效果越差。M>12.0,(实验中取M=18.0),工频干扰滤除较干净,但出现QRS波严重削峰,如图4所示。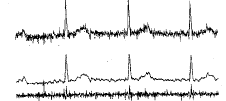
, 百拇医药
图4 Levkov法滤波产生削峰的ECG波形
Fig.4 Levkov filtering method brings reducing strength
方法改进
我们认为,仅仅依靠M值的调整,并不能完全解决问题,应该加入另一个限制条件来解决。既要使M取值大一些,较好的实现滤波,又要保持不失真。我们引入QRS波开关控制的方法,即在Levkov滤波基础上,加入QRS识别的开关函数法。其具体实现过程如下:首先对ECG信号微分,并设定阈值进行识别,若满足一定条件,认为是QRS 波,滤波是单独处理,否则按照Levkov法[此时,M可取值较大,M=18(0)]进行滤波。算法中,我们采用自适应调整阈值法判别QRS波,阈值能很好地跟随信号变化,而又不会把干扰当作QRS误检。当检测到一QRS 波后,求出其最大值,调整阈值,并置一标志,作为Levkov法中单独处理QRS波的依据。程序流程图如图5所示 ,图6,图7分别是在噪声较弱和噪声较强时的滤波效果图,由图可见,新的Levkov滤波法对于抑制强、弱噪声效果都很好,并且对信号几乎没有削峰。
, http://www.100md.com
图5 程序波程图
Fig.5 Flow diagram of progam
图6 噪声较弱时新的Levkov滤波
Fig.6 Levkov method at weak noise
图7 噪声较强时新的Levkov滤波
Fig.7 Levkov method at powerful noise
结 论
比较上述几种滤波法,可得出如下结论:平滑滤波算法简单,易于快速时实处理,但是伴有严重的削峰现象。NOTCH滤波效果较好,但不能实现时实滤波,并且当干扰频率有漂移时,滤波效果较差。自适应滤波效果较好,并且能够跟随干扰频率的变化,但自适应滤波计算量大,并且需要一段学习时间。
, 百拇医药
这种新的Levkov滤波法在滤除ECG信号中的50Hz工频干扰时,克服了前几种滤波法的缺点,同时又兼有各法的优点。如算法简单,易于实时处理,能够跟随噪声频率的变化,并且对QRS波没有削峰。通过几十例的实验表明,滤波效果令人满意,具有广阔的应用前景。
Address reprint requests to:SUN Jing-xia. Institute of Space Medico-Engineering, Beijing 100094,China
[参考文献]
[1] Xue Q,Hu YH,Tompkins W. Neural-network-based adaptive matched filtering for detection[J]. IEEE Trans on BME,1992,39:317~318
, 百拇医药 [2] Barbaro V,Bartolinia P, Fierli M. New algorithm for the detection of the ECG fiducial point in the averaging technique[J]. IEEE MBEC,1991,21:129~131
[3] Willis JT.C Language Examples and Laboratory Experiments for the IBM PC[M],1993:132
[4] ZHAO Jie,HUA Mei.A simple algorithm for removal of base-line wander and power-line interference from ECG[J].Chinese Journal of Medical Instrumentation,1991,15:262~263
, 百拇医药
赵 捷,华 玫.一种滤除ECG基线漂移和交流干扰的简单算法[J].中国医疗器械,1991,15:262~263
[5] TANG Yu.Simple integral coefficient recursive digital filter and its application in biomedicine (2)[J].Chinese Journal of Medical Instrumentation,1989,13:226~228
唐 渝.简单整系数递归数字滤波器及其在生物医学中的应用(二)[J].中国医疗器械杂志,1989,13:226~228
[6] 段新昱,林家瑞,司海芹.ECG监视过程中的削噪问题[J].国外医学生物医学工程分册,1992,15(3):131~135
收稿日期:1999-09-06, 百拇医药
单位:孙京霞 白延强(航天医学工程研究所,北京 100094);杨玉星(华中理工大学,湖北 430074)
关键词:心电信号;模板;工频干扰;滤波
航天医学与医学工程000310摘要: 目的 探讨一种用于抑制心电信号中50 Hz工频干扰的新方法。 方法 在Levkov滤波法的基础上加入QRS开关函数,并用此法与几种常用的滤波方法进行比较。 结果 该方法算法简单,处理速度快,对强、弱噪声滤波效果都较好。 结论 该方法对于抑制心电信号中50 Hz工频干扰有很好的应用前景。
中图分类号:R540.41 文献标识码:A
文章编号:1002-0837(2000)03-0196-04
, http://www.100md.com
An Improved Levkov Method for Filtering 50 Hz Interference in ECG Signals
SUN Jing-xia,BAI Yan-qiang,YANG Yu-xing
Abstract: Objective To find a new method for repressing the 50 Hz power-line interference in ECG signals. Method An improved method based on Levkov filtering method and inserted QRS switch function, several ordinary methods were compared with it. Result This method had a simple algorithm, fast processing speed and good result of filtering both strong and weak interference. Conclusion This method provides a good base for further disposing.
, 百拇医药
Key words:ECG signals;templet;power-line interference;filtration
在采集ECG信号过程中,常常受到各种干扰,其中50 Hz工频干扰是最主要的一种。如何有效抑制50 Hz工频干扰,是处理心电信号的首要任务。目前比较常用的方法有:平滑滤波,中心频率固定的带阻滤波,自适应滤波,Levkov滤波等。
1984年,Levkov首先提出对ECG信号的线性段和非线性段采用不同处理方式的数字滤波法[1]。1988年Christov改进该算法[2],引入ECG信号的线性段判据M来加快滤波的速度。在线性段判断过程中,M的选择非常关键,M取值较小,滤波效果差,M取值较大,滤波效果好,但削峰严重。对此,我们引入QRS波开关控制的方法,即在Levkov基础上,加入QRS识别的开关函数法。此法既比较好地实现滤波,又保持波形不失真。经实际检验,该方法滤波效果好,对于抑制心电信号中50 Hz工频干扰有很好的应用前景。
, http://www.100md.com
几种常用的滤波法
下面介绍的几种滤波都是在采样频率为200 Hz,工频干扰为50 Hz的条件下实现的。
平滑滤波 平滑滤波是数字滤波方法中较早被人们采用的方法[3],该方法算法简单,处理速度快,滤波效果较好,但也存在明显不足,通频带较窄,影响有用信号的分析。滤波效果如图1所示。

图1 平滑滤波示意图
Fig.1 Smooth filtering method
A:first ECG signal;B:after filtering ECG signal;C:elimination interference
, 百拇医药
其传递函数为:

差分方程为:
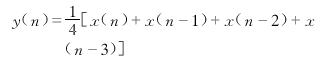
NOTCH滤波 NOTCH滤波器,又称简单整系数带阻滤波器,其原理为用一个全通网络减去一个具有相同传输延迟和增益的窄带线形相位FIR滤波器的输出,得到一个具有尖锐陷波特性的陷波滤波器[4,5]。
NOTCH滤波器传递函数为:
H(z)=z-148-(1+z-100-z-200-z-300)/[100。(1-z-4)]
, http://www.100md.com
差分方程为:y(n)=y1(n)-y2(n)/100
其中:y1(n)=x(n-148)
y2(n)=x(n)+x(n-100)-x(n-
200)-x(n-300)+y(n-4)
y1(n)为全通网络输出,y2(n)为窄带带通滤波器输出,y(n)为NOTCH滤波器输出。滤波效果如图2所示。

图2 NOTCH滤波法
Fig.2 Notch filtering method
, http://www.100md.com
自适应滤波 设原始输入x(n)为信号与噪声w(n)之和:x(n)=s(n)+w(n)

滤波后输出为y(n)。
其中e(n)为误差,d(n)为预期信号,h(n)为FIR各阶系数,N为FIR的阶数,M为数据长度。d应该随着信号变化不断调整,使E[e2]最小[6,7]。滤波效果如图3所示。

图3 自适应滤波法
Fig.3 Self-adapting filtering method
新的Levkov滤波
, http://www.100md.com
1984年,Levkov首先提出对ECG信号的线性段和非线性段采用不同处理方式的数字滤波方法。1988年Christov对该算法改进,引入ECG信号的线性段判据M来加快滤波的速度。用该方法滤波,它要求原始ECG信号满足以下两个条件:(1)采样频率fs应是工频干扰的整数倍;(2)在一个工频干扰周期T内,工频干扰采样点的幅值的代数和为0。在滤波过程中首先要识别出一个线性段,该线性段滤波后的值为这个线性段原始数据的平均值。同时求出工频干扰的值作为非线性段的工频干扰的模板。而在非线性段,其真值是用原始数据减去在临近线性段求得的干扰模板值。
Levkov滤波原理 设原始信号为Si,干扰信号为Ni,包含噪声的信号为Xi=Si+Ni, i=0,1,2,…, S0,S1,S2,S3为线性段信号,对于200 Hz采样率,相邻间距为5 ms,故:
S4-S3=S3-S2=S2-S1=S1-S0=d;
, 百拇医药
N0+N1+N2+N3=0;N0=N4;d为线性段上相邻点间的差值。
X0+X1+X2+X3
=S0+S1+S2+S3+N0+N1+N2+N3
=S1-d+S1+S1+d+S1+2d=4S1+2d
X4-X0=S4+N4-S0-N0=4d;
, http://www.100md.com
所以,T1时刻,信号和噪声分别是:
S1=[(X0+X1+X2+X3)-(X4-X0)/2]/4;
N1=X1-S1;
对于线性段可按上述模式处理。当出现非线性段时,考虑到工频干扰的相位在短时间内不会有过大的变化,可用最近计算出的与当前点同相位处的噪声作为当前噪声的预测值,则当前的信号值为: S1=X1-N1; 我们用上述改进的Levkov法(即Christov法)进行滤波,实验中发现,对于有些心电波形,滤波效果不好。分析其原因是:在该算法中引入M用来判定线性段和非线性段的指标,是滤波方法中的关键因素。Christov在fs= 400 Hz,工频干扰f=50 Hz情况下经过大量(大于200次)实验,认为M=12.0 是较为理想的值。而我们发现对于噪声较大的ECG波形,该方法滤波效果不好,这与M取值有关。M值越小,滤波效果越差。M>12.0,(实验中取M=18.0),工频干扰滤除较干净,但出现QRS波严重削峰,如图4所示。

, 百拇医药
图4 Levkov法滤波产生削峰的ECG波形
Fig.4 Levkov filtering method brings reducing strength
方法改进
我们认为,仅仅依靠M值的调整,并不能完全解决问题,应该加入另一个限制条件来解决。既要使M取值大一些,较好的实现滤波,又要保持不失真。我们引入QRS波开关控制的方法,即在Levkov滤波基础上,加入QRS识别的开关函数法。其具体实现过程如下:首先对ECG信号微分,并设定阈值进行识别,若满足一定条件,认为是QRS 波,滤波是单独处理,否则按照Levkov法[此时,M可取值较大,M=18(0)]进行滤波。算法中,我们采用自适应调整阈值法判别QRS波,阈值能很好地跟随信号变化,而又不会把干扰当作QRS误检。当检测到一QRS 波后,求出其最大值,调整阈值,并置一标志,作为Levkov法中单独处理QRS波的依据。程序流程图如图5所示 ,图6,图7分别是在噪声较弱和噪声较强时的滤波效果图,由图可见,新的Levkov滤波法对于抑制强、弱噪声效果都很好,并且对信号几乎没有削峰。

, http://www.100md.com
图5 程序波程图
Fig.5 Flow diagram of progam

图6 噪声较弱时新的Levkov滤波
Fig.6 Levkov method at weak noise

图7 噪声较强时新的Levkov滤波
Fig.7 Levkov method at powerful noise
结 论
比较上述几种滤波法,可得出如下结论:平滑滤波算法简单,易于快速时实处理,但是伴有严重的削峰现象。NOTCH滤波效果较好,但不能实现时实滤波,并且当干扰频率有漂移时,滤波效果较差。自适应滤波效果较好,并且能够跟随干扰频率的变化,但自适应滤波计算量大,并且需要一段学习时间。
, 百拇医药
这种新的Levkov滤波法在滤除ECG信号中的50Hz工频干扰时,克服了前几种滤波法的缺点,同时又兼有各法的优点。如算法简单,易于实时处理,能够跟随噪声频率的变化,并且对QRS波没有削峰。通过几十例的实验表明,滤波效果令人满意,具有广阔的应用前景。
Address reprint requests to:SUN Jing-xia. Institute of Space Medico-Engineering, Beijing 100094,China
[参考文献]
[1] Xue Q,Hu YH,Tompkins W. Neural-network-based adaptive matched filtering for detection[J]. IEEE Trans on BME,1992,39:317~318
, 百拇医药 [2] Barbaro V,Bartolinia P, Fierli M. New algorithm for the detection of the ECG fiducial point in the averaging technique[J]. IEEE MBEC,1991,21:129~131
[3] Willis JT.C Language Examples and Laboratory Experiments for the IBM PC[M],1993:132
[4] ZHAO Jie,HUA Mei.A simple algorithm for removal of base-line wander and power-line interference from ECG[J].Chinese Journal of Medical Instrumentation,1991,15:262~263
, 百拇医药
赵 捷,华 玫.一种滤除ECG基线漂移和交流干扰的简单算法[J].中国医疗器械,1991,15:262~263
[5] TANG Yu.Simple integral coefficient recursive digital filter and its application in biomedicine (2)[J].Chinese Journal of Medical Instrumentation,1989,13:226~228
唐 渝.简单整系数递归数字滤波器及其在生物医学中的应用(二)[J].中国医疗器械杂志,1989,13:226~228
[6] 段新昱,林家瑞,司海芹.ECG监视过程中的削噪问题[J].国外医学生物医学工程分册,1992,15(3):131~135
收稿日期:1999-09-06, 百拇医药