对Polya分布的两点注释断奶仔猪肠道菌群的研究
作者：孙高 丁雁 郭海强 刘延龄
单位：中国医科大学(110001)
关键词：
中国卫生统计990127 Polya分布是研究弱传播现象的离散分布，但与之有关的问题中有两点分别值得商榷和补充，本文的目的就在这里。
一、Polya分布产生的背景
这个分布产生于以下概型：在一个罐中装有N个白球和黑球，二者之比为p∶q，p+q=1，从中任取一个球后，便添加与之同色球d个放回罐中再取，如此取n次得到的白球数x,在Np=m,Nd=δ固定，n→∞,p→0,d→0的条件下，所服从的分布就称Polya分布〔1〕。其中m是白球总体均数，δ称传播系数。这里值得商榷的地方是Np=m，Nd=δ，n→∞,p→0,d→0。我们认为应改成np=m,nd=δ,n→∞。因为在后面的条件下，很自然地有d→0，代表这是一种弱传播，而且也只有在这种条件下，才能证明：取n次得到的x个白球的概率：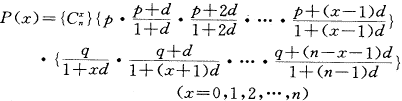
, http://www.100md.com
(1)
的极限是Polya分布的概率函数：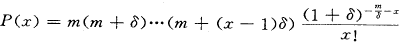
(2)
事实上，把式(1)右边前两个{}内各因子分别除以和乘以n，取极限就可以得到式(2)右边除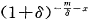
各部分。把(1)式右边最后的{}各因子取对数，将其和同时除以和乘以d并把乘d后的总和用积分代替，最后在前述条件下应用洛必大法则便可得到(-
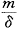-x)ln(1+δ)，取此式的指数函数便得到剩下的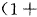
。
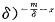, 百拇医药
二、Polya分布和负二项分布的关系
这个分布和Poisson分布的关系已有报道，事实上，Polya分布在δ→0时的极限就是总体均数为m的Poisson分布，这既容易理解(因为后者是代表独立小概率事件发生的规律)，也容易证明(这只需要利用
。但它和负二项分布有什么关系却未见报道，下面想就此作些补充。
负二项分布是一种离散型分布，可用于寄生虫学、医学昆虫学、微生物学以及流行病学等的研究〔2〕，其概率函数：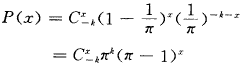
(3)
, 百拇医药 式中k>0，0<π<1，x=0，1，2，…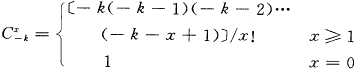
从负二项分布的概率函数表达式看，它们刚好是二项式〔
+(1-)〕-k形式上展开的各项，因此从数学上容易理解，但其产生的背景是什么?k、x的实际意义及应用于所提到学科哪类现象研究却没有说明，因此研究它和Polya分布的关系也许有助于这些问题的解决。
其实，负二项分布和Polya分布是同一分布，这只要令
，并将之代入负二项分布概率函数(3)马上会得到Polya分布的概率函数(2)。事实上，此时的负二项分布概率函数(3)为:
, 百拇医药
三、两个注释的应用
负二项分布和Polya分布的这种联系及后者产生的背景不仅使负二项产生的背景及其中的参数实际意义获得了解释，而且使负二项分布所研究的实际现象更加具体，即弱传播现象。应当指出，这种弱传播现象不仅包括同一家族患结核这种有传染性现象的疾病，还包括龋齿、工厂事故、同一夫妇子女的死亡、特定区内肠伤寒及一年内感冒罹患等。一旦在某处有某些事件发生，受其影响，在其周围易有相同事件发生这类情况。
参考文献
1.丁道芳，刘延龄编译.临床统计学.北京：人民卫生出版社，1986：26
2.杨树勤主编.中国医学百科全书*医学统计学.上海：上海科技出版社，1982：25
中国微生态学杂志 2000年第2期第12卷 论 著
断奶仔猪肠道菌群的研究
作者：禹慧明 廖玲 陈平洁 陈庄 刘敬顺 谢明权
单位：禹慧明 廖玲 陈平洁(广东省农业科学院畜牧研究所，广东 广州 510640)；陈庄 刘敬顺 谢明权(广东省农业科学院，广东 广州 510640)
关键词：断奶仔猪；肠道菌群., 百拇医药
单位：中国医科大学(110001)
关键词：
中国卫生统计990127 Polya分布是研究弱传播现象的离散分布，但与之有关的问题中有两点分别值得商榷和补充，本文的目的就在这里。
一、Polya分布产生的背景
这个分布产生于以下概型：在一个罐中装有N个白球和黑球，二者之比为p∶q，p+q=1，从中任取一个球后，便添加与之同色球d个放回罐中再取，如此取n次得到的白球数x,在Np=m,Nd=δ固定，n→∞,p→0,d→0的条件下，所服从的分布就称Polya分布〔1〕。其中m是白球总体均数，δ称传播系数。这里值得商榷的地方是Np=m，Nd=δ，n→∞,p→0,d→0。我们认为应改成np=m,nd=δ,n→∞。因为在后面的条件下，很自然地有d→0，代表这是一种弱传播，而且也只有在这种条件下，才能证明：取n次得到的x个白球的概率：
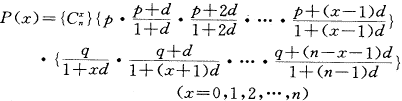
, http://www.100md.com
(1)
的极限是Polya分布的概率函数：
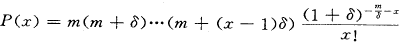
(2)
事实上，把式(1)右边前两个{}内各因子分别除以和乘以n，取极限就可以得到式(2)右边除
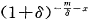各部分。把(1)式右边最后的{}各因子取对数，将其和同时除以和乘以d并把乘d后的总和用积分代替，最后在前述条件下应用洛必大法则便可得到(-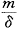-x)ln(1+δ)，取此式的指数函数便得到剩下的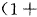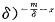。, 百拇医药
二、Polya分布和负二项分布的关系
这个分布和Poisson分布的关系已有报道，事实上，Polya分布在δ→0时的极限就是总体均数为m的Poisson分布，这既容易理解(因为后者是代表独立小概率事件发生的规律)，也容易证明(这只需要利用
。但它和负二项分布有什么关系却未见报道，下面想就此作些补充。负二项分布是一种离散型分布，可用于寄生虫学、医学昆虫学、微生物学以及流行病学等的研究〔2〕，其概率函数：
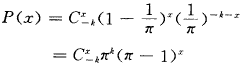
(3)
, 百拇医药 式中k>0，0<π<1，x=0，1，2，…
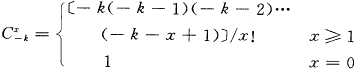
从负二项分布的概率函数表达式看，它们刚好是二项式〔
+(1-)〕-k形式上展开的各项，因此从数学上容易理解，但其产生的背景是什么?k、x的实际意义及应用于所提到学科哪类现象研究却没有说明，因此研究它和Polya分布的关系也许有助于这些问题的解决。其实，负二项分布和Polya分布是同一分布，这只要令
，并将之代入负二项分布概率函数(3)马上会得到Polya分布的概率函数(2)。事实上，此时的负二项分布概率函数(3)为:, 百拇医药
三、两个注释的应用
负二项分布和Polya分布的这种联系及后者产生的背景不仅使负二项产生的背景及其中的参数实际意义获得了解释，而且使负二项分布所研究的实际现象更加具体，即弱传播现象。应当指出，这种弱传播现象不仅包括同一家族患结核这种有传染性现象的疾病，还包括龋齿、工厂事故、同一夫妇子女的死亡、特定区内肠伤寒及一年内感冒罹患等。一旦在某处有某些事件发生，受其影响，在其周围易有相同事件发生这类情况。
参考文献
1.丁道芳，刘延龄编译.临床统计学.北京：人民卫生出版社，1986：26
2.杨树勤主编.中国医学百科全书*医学统计学.上海：上海科技出版社，1982：25
中国微生态学杂志 2000年第2期第12卷 论 著
断奶仔猪肠道菌群的研究
作者：禹慧明 廖玲 陈平洁 陈庄 刘敬顺 谢明权
单位：禹慧明 廖玲 陈平洁(广东省农业科学院畜牧研究所，广东 广州 510640)；陈庄 刘敬顺 谢明权(广东省农业科学院，广东 广州 510640)
关键词：断奶仔猪；肠道菌群., 百拇医药