应用灰色模型预测病毒性肝炎发病率
作者：解西伦 张陆仁 杨桂启
单位：兖州市卫生防疫站(272000)
关键词：
中国卫生统计990110 本文试用GM(1,1)模型对兖州市1990～1995年病毒性肝炎进行建模拟合，并对1996年发病率进行预测。
灰色预测模型建立
本文依据文献〔1〕提供的方法建立预测模型。
一、数据处理
设原始数据序列为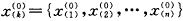
k=1,2，…，n
, 百拇医药
经一次累加生成数据
二、建立模型
GM(1，1)模型是按累加生成数据建立的微分方程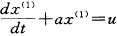
，其中a和u为待定系数。
按微分方程的求解方法得a和u满足下列方程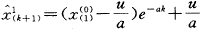
，式中u是内生变量和待辩识参数，则有辩识参数列
。
由于GM(1，1)模型的微分方程仅是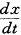
与x的线性组合，即有通式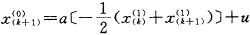
, 百拇医药
当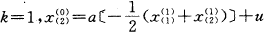
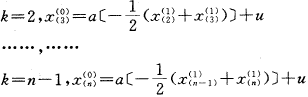
再用最小二乘法原理对
求解得=(BTB)-1BTYN
其中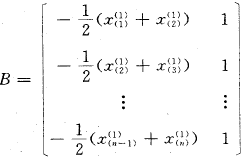
T表示矩阵转置，-1表示逆矩阵。
, http://www.100md.com
计算结果
兖州市1990～1995年病毒性肝炎发病率见表1。
表1 兖州市1990～1995年病毒性肝炎发病率(1/10万) 年份
1990
1991
1992
1993
1994
1995
时序k+1
1
2
, http://www.100md.com
3
4
5
6
x(0)
53.58
43.98
36.10
29.45
15.44
11.16
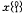
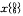
, http://www.100md.com
一、一次累加生成数据
按公式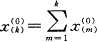
得累加生成数据(表2)。
表2 原始数据一次累加生成数据
1
2
3
4
5
6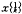
53.58
, 百拇医药
97.56
133.66
163.11
178.55
189.71
二、确定数据矩阵B和YN
三、计算(BTB)-1
四、求参数列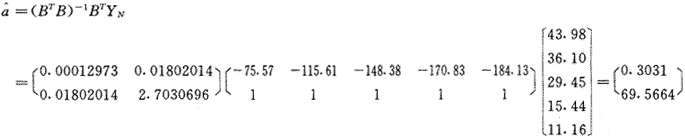
, 百拇医药
五、确定模型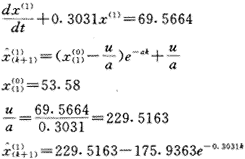
六、精度检验
为确保模型的预测精度，需进行残差检验。
生成模型计算数据 实际值
表3 残差的计算 时序k+1
估计的原始数据
实际数据
残差
2
46.66
, http://www.100md.com
43.98
2.68
3
34.53
36.10
-1.57
4
24.59
29.45
-4.86
5
17.79
15.44
, http://www.100md.com
2.35
6
13.76
11.16
2.60
七、外推预测
应用所得模型，预测k+1=7,8,即预测1996年，1997年发病率。
讨 论
GM(1，1)模型根据传染病历年发病率，将无规律的原始数据经一次累加变为较有规律的生成数据后再建立模型方程，并对未来的发展趋势进行预测。它不受一般统计模型对原始数据种种要求的约束〔2〕，且考虑影响因素较少，比较适用于流行因素较稳定的疾病〔3〕，因而具有较强的实用性。
, 百拇医药
本文运用该模型对兖州市1990～1995年病毒性肝炎发病率进行了拟合与外推预测，从最后的检验结果看，残差较小，拟合效果较为满意。外推预测1996年发病率为10.18，实际值为9.74，相差0.44，其相对误差为4.56%，说明预测效果良好。这对掌握病毒性肝炎的流行规律，制订相应地防治措施具有重要意义。
参考文献
1.章杨熙编著.医学统计预测.第1版.北京：中国科学技术出版社，1995：90.
2.王万平.灰色数列预测模型在防痨工作中的应用.中国卫生统计 1990，7(3)：56.
3.钱俊英，等.灰色预测方法——对野鼠型出血热预测的探讨.中国公共卫生，1992，8(4)：160., http://www.100md.com
单位：兖州市卫生防疫站(272000)
关键词：
中国卫生统计990110 本文试用GM(1,1)模型对兖州市1990～1995年病毒性肝炎进行建模拟合，并对1996年发病率进行预测。
灰色预测模型建立
本文依据文献〔1〕提供的方法建立预测模型。
一、数据处理
设原始数据序列为
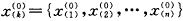
k=1,2，…，n
, 百拇医药
经一次累加生成数据
二、建立模型
GM(1，1)模型是按累加生成数据建立的微分方程
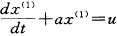，其中a和u为待定系数。按微分方程的求解方法得a和u满足下列方程
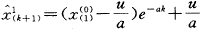，式中u是内生变量和待辩识参数，则有辩识参数列。由于GM(1，1)模型的微分方程仅是
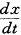与x的线性组合，即有通式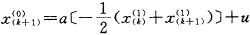, 百拇医药
当
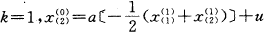
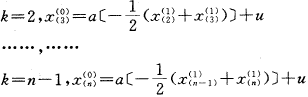
再用最小二乘法原理对
求解得=(BTB)-1BTYN其中
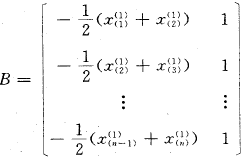
T表示矩阵转置，-1表示逆矩阵。
, http://www.100md.com
计算结果
兖州市1990～1995年病毒性肝炎发病率见表1。
表1 兖州市1990～1995年病毒性肝炎发病率(1/10万) 年份
1990
1991
1992
1993
1994
1995
时序k+1
1
2
, http://www.100md.com
3
4
5
6
x(0)
53.58
43.98
36.10
29.45
15.44
11.16
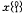
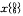
, http://www.100md.com
一、一次累加生成数据
按公式
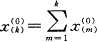得累加生成数据(表2)。表2 原始数据一次累加生成数据
1
2
3
4
5
6
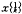
53.58
, 百拇医药
97.56
133.66
163.11
178.55
189.71
二、确定数据矩阵B和YN
三、计算(BTB)-1
四、求参数列
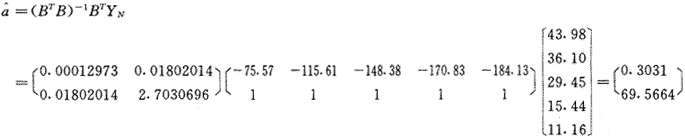
, 百拇医药
五、确定模型
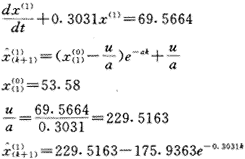
六、精度检验
为确保模型的预测精度，需进行残差检验。
生成模型计算数据 实际值
表3 残差的计算 时序k+1
估计的原始数据
实际数据
残差
2
46.66
, http://www.100md.com
43.98
2.68
3
34.53
36.10
-1.57
4
24.59
29.45
-4.86
5
17.79
15.44
, http://www.100md.com
2.35
6
13.76
11.16
2.60
七、外推预测
应用所得模型，预测k+1=7,8,即预测1996年，1997年发病率。
讨 论
GM(1，1)模型根据传染病历年发病率，将无规律的原始数据经一次累加变为较有规律的生成数据后再建立模型方程，并对未来的发展趋势进行预测。它不受一般统计模型对原始数据种种要求的约束〔2〕，且考虑影响因素较少，比较适用于流行因素较稳定的疾病〔3〕，因而具有较强的实用性。
, 百拇医药
本文运用该模型对兖州市1990～1995年病毒性肝炎发病率进行了拟合与外推预测，从最后的检验结果看，残差较小，拟合效果较为满意。外推预测1996年发病率为10.18，实际值为9.74，相差0.44，其相对误差为4.56%，说明预测效果良好。这对掌握病毒性肝炎的流行规律，制订相应地防治措施具有重要意义。
参考文献
1.章杨熙编著.医学统计预测.第1版.北京：中国科学技术出版社，1995：90.
2.王万平.灰色数列预测模型在防痨工作中的应用.中国卫生统计 1990，7(3)：56.
3.钱俊英，等.灰色预测方法——对野鼠型出血热预测的探讨.中国公共卫生，1992，8(4)：160., http://www.100md.com