两水平方差成分模型与线性回归模型关系的探讨利用食品厂的废料发酵生产饲用微生物添加剂联合应用回春生、促菌生治疗小儿迁延性肠炎疗效观察
作者:李晓松 倪宗瓒
单位:华西医科大学卫生统计学教研室(成都 610041)
关键词:层次结构数据;方差成分模型;线性回归模型;单位内相关系数
中国卫生统计990105 【提 要】 目的 探讨对于具有两个水平层次结构的数据拟合方差成份模型与线性回归模型的关系。方法 通过三类传统线性回归模型与两水平方差成份模型参数估计的对比,分析其内在联系。结果 线性回归模型参数估计以及估计的稳定性与自变量在水平2单位间和水平2单位内的变异大小有关,线性因归模型与方差成分模型参数估计及其稳定性的关系与水平2残差方差或单位内相关系数大小有关。结论 当数据具有层次结构特征时,三类线性回归模型均存在问题,方差成分模型可将线性回归模型的单一随机误差项分解到与数据层次结构相对应的各水平上,并估计水平2单位的随机效应。
Research into the relationship between the 2 level variance component model and the linear regression models.
, http://www.100md.com
Li Xiaosong,Ni Zongzan.
Department of Health Statistics,West China Universith of Medical Sciences(Chengdu 610041)
【Abstract】 Objective to explore the relationship between the variance component model and the linear regression models in fitting 2 level hierarchically-structured data.Methods by comparative analysis for the parameter estimates between three linear regression mdels and 2 level variance component moddel.Results the parameter estimates and it's stability of linear regression models is associated with the variation of explanatory variable between and within level 2units,and the relationship of parameter estimates and it's stability between linear regression models and variance component model is associated with level 2 residual variance or intatra-unit correlation.Conclusion the three linear regression models are inappropriate whten data are hierarchically structured,and both the single random error term of linear regression model can be decomposed into corresponding levels of hierarchical structure,and the randowm effects of level 2 units can be estimated by variance component model.
, 百拇医药
Key words hierachically-structured data variance component model linear regression models intra-unit correlation
多水平统计模型(multilevel statistical models)是英、美等发达国家教育学界80年代中后期发展起来的一门多元统计分析新技术,可有效处理传统多元统计方法难以分析的具有层次结构特征的数据(hierarchically structured data),是目前国际上统计学研究中一个新兴而重要的领域〔1〕。在临床医学,预防医学以及其它学科领域存在大量层次结构数据,因而多水平模型在这些领域具有广阔的应用前景。两水平方差成分模型是多水平模型中最基本的模型,而传统的线性回归模型仍是处理不具层次结构特征数据的有力工具。对两水平方差成分模型与各类传统线性回归模型之间内在联系的探讨,有助于对数据结构和多水平模型的认识和正确应用。
, http://www.100md.com
基本模型
现假定一具有两水平层次结构特征的数据,水平2单位为相应总体的随机样本。模型中有一个解释变量,yij、xij均为水平1变量,且β1在水平2单位间不存在变异。以符号Txx、Tyy、Txy分别表示x、y以及x与y的总的离均差平方和、积和;Axx、Ayy、Axy分别表示x、y以及x与y的水平2单位间离均差平方和、积和;Wxx、Wyy、Wxy分别表示x、y以及x与y的水平2单位内离均差平方和、积和。
对于上述数据,我们可建立以下四类模型:水平1的合并模型、水平2的聚集模型、水平2单位的固定效应模型以及两水平方差成份模型。
, 百拇医药 1.水平1的合并模型
以水平1单位为分析的基本单位,即将水平1单位合并在一起,忽略水平2单位对反应变量的效应。模型可表达为: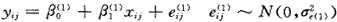
j=1,2,…,m示水平2单位,i=1,2,…,nj示水平1单位。括弧中的数字示模型编号,这里示模型1,以下同此。
根据最小二乘法原理,可得到模型参数及其方差的估计: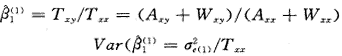
2.水平2的聚集模型
将水平1单位的特征包括反应变量和解释变量聚集为相应的水平2单位的特征,即计算各水平2单位所属的所有水平1单位的某种统计量如均数,以水平2单位为分析的基本单位。模型及其参数估计为: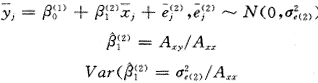
, http://www.100md.com
3.水平2单位的固定效应模型
对每个水平2单位拟合固定参数βoj,并假定一个普通的水平2单位内残差方差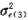 ,该模型拟合m条平行的回归线。模型及其参数估计为:
,该模型拟合m条平行的回归线。模型及其参数估计为: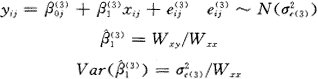
4.两水平方差成分模型
基本的模型结构与模型假设为:
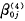 为随机变量,假定:
为随机变量,假定: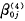 =
=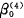 +u0j
+u0j
, 百拇医药
代入式(4)有:yij=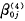 +
+ xij+u0j+eij
xij+u0j+eij
这里,u0j亦为随机变量:
u0j~N(0, )
)
水平1残差eij即线性回归模型中通常的残差项,eij~N(0,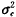 )。
)。
, 百拇医药
与传统线性回归模型不同的是,两水平方差成分模型具有两个残差项,它属模型随机部分的结构。
固定参数的估计为: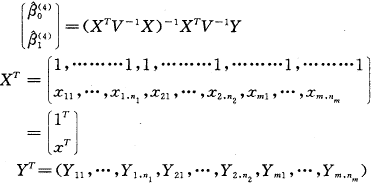
V为向量Y的协方差阵,这为分块对角阵,每个块对应于一个水平2单位:
根据线性代数原理,可得到V的逆阵为: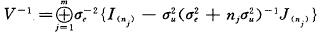
因此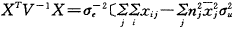
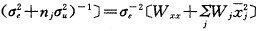
, 百拇医药
式中: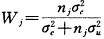
相似地:
因此:
式中,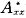 和
和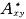 为加权的离均差平方和与积和,权重即为Wj。
为加权的离均差平方和与积和,权重即为Wj。
讨 论
1.线性回归模型参数估计间的联系
, 百拇医药
现定义一指标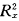 反映x在水平2单位间变异占总变异的比例,则
反映x在水平2单位间变异占总变异的比例,则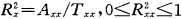 。进一步可导出:
。进一步可导出: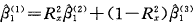 。可见。
。可见。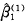 的估计介于
的估计介于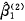 和
和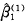 之间:如果Axx→0,那么
之间:如果Axx→0,那么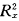 →0,
→0,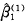 →
→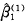 ,因Var(
,因Var(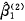 )=
)=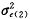 /Axx,故
/Axx,故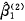 的估计不稳定;如果Wxx→0,那么
的估计不稳定;如果Wxx→0,那么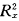 →1,
→1,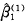 →
→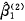 ,因Var(
,因Var(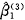 )=
)=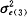 /Wxx,故
/Wxx,故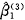 的估计不稳定。
的估计不稳定。
, 百拇医药
2.两水平方差成分模型与线性回归模型参数估计的联系
由上述推导可见,两水平方差成分模型与传统线性回归模型参数估计的联系与区别关键在于权重Wj。
①如果 =0,则Wj=nj,
=0,则Wj=nj,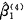 =
=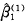 =Txy/Txx,Var(
=Txy/Txx,Var(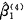 )=
)=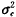 /Txx=Var(
/Txx=Var(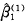 ),在这种情形下,水平2单位对反应变量无效应或效应相同,方差成分模型等价于水平1合并模型;如果
),在这种情形下,水平2单位对反应变量无效应或效应相同,方差成分模型等价于水平1合并模型;如果 相对于
相对于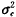 增加,则Wj趋近于0,
增加,则Wj趋近于0,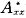 和
和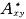 亦趋近于0,
亦趋近于0,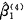 →
→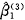 =WxyWxx,Var(
=WxyWxx,Var(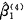 )→(
)→( +
+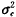 )/Wxx,在这种情形下,参数估计不依赖于水平2单位的间信息,方差成份模型的参数估计趋近于水平2单位固定效应模型;此外,从前面参数估计的表达式还可看出,水平2单位内的信息Wxx和Wxy对于模型固定参数的估计总是重要的。因此,未用到水平1单位信息的方法如水平2聚集模型在统计上是无效的(inefficient)〔1〕。
)/Wxx,在这种情形下,参数估计不依赖于水平2单位的间信息,方差成份模型的参数估计趋近于水平2单位固定效应模型;此外,从前面参数估计的表达式还可看出,水平2单位内的信息Wxx和Wxy对于模型固定参数的估计总是重要的。因此,未用到水平1单位信息的方法如水平2聚集模型在统计上是无效的(inefficient)〔1〕。
, 百拇医药
②我们从另一个角度进一步考察这一问题。两水平方差成分模型反应变量的方差为:
Var(yij|β0,β1,xij)=Var(uoj+eij)= +
+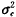
同一水平2单位所属的两个水平1单位(用i1,i2表示)间的协方差为:
Cov(u0j+ei1j,u0j+ei2j)=Cov(u0j,u0j)=
, 百拇医药
相关则为: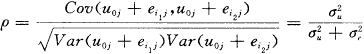
ρ即“单位内相关系数”(intra-unit correlation),反映了同一水平2单位内水平1单位的相似性或聚集性,测量了水平2单位间变异在总变异中所占的比例〔2〕。可以发现,Wj与ρ具有一定联系: =0,ρ=0,意味着数据不存在层次结构特征,此时Wj=nj;
=0,ρ=0,意味着数据不存在层次结构特征,此时Wj=nj; 相对于
相对于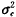 增加,ρ趋近于1,意味着数据层次结构特征明显,则Wj趋近于0,这与前面推论的情形是一致的。此外,一种极端的情形是,每个水平2单位中只有一个水平1单位即nj=1,此时仍可估计水平2残差方差
增加,ρ趋近于1,意味着数据层次结构特征明显,则Wj趋近于0,这与前面推论的情形是一致的。此外,一种极端的情形是,每个水平2单位中只有一个水平1单位即nj=1,此时仍可估计水平2残差方差 ,且ρ与Wj满足下式:ρ=(
,且ρ与Wj满足下式:ρ=( /σ2e)Wj,
/σ2e)Wj, /
/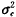 即方差成分比。
即方差成分比。
, 百拇医药
如果数据具有层次结构特征,那么,除非x完全解释了y在水平2单位内的相似性或聚集性,否则y的残差相关,此时,三类线性回归模型都是不适宜的,且当残差存在复杂变异时,线性回归模型更难以探讨与之相关的因素。实际上,线性回归模型中单一的随机误差项包含了数据层次结构中高水平单位(如水平2单位)的随机效应与误差,多水平统计模型则将这种随机效应与误差分解到与数据层次结构相对的各水平上,并提供了拟合各水平复杂误差结构的可能性。
(致谢伦敦大学多水平模型课题组杨珉研究员提供的帮助)
参考文献
1.Goldstein,H.Multilevel Statistical Models.London:Edward Arnold.1995
2.杨珉.多元分析的发展——多水平模型简介.中国卫生统计.1994;11(5):32
, http://www.100md.com
中国微生态学杂志 2000年第5期第12卷 论 著
利用食品厂的废料发酵生产饲用微生物添加剂
作者:莫美华 林创华 冼毅和 邓宏益 谢秀菊
单位:莫美华 林创华 冼毅和 邓宏益(华南农业大学 食品系微生物教研室,广东广州510642);谢秀菊(广州市农科所,广东广州510308)
关键词:饲用微生物添加剂;发酵;啤酒糟.
中国微生态学杂志 2000年第5期第12卷 临床研究
联合应用回春生、促菌生治疗小儿迁延性肠炎疗效观察
作者:李凌媛 殷铮
单位:昆明市儿童医院, 云南 昆明650032
关键词:回春生;促菌生;迁延性肠炎., http://www.100md.com
单位:华西医科大学卫生统计学教研室(成都 610041)
关键词:层次结构数据;方差成分模型;线性回归模型;单位内相关系数
中国卫生统计990105 【提 要】 目的 探讨对于具有两个水平层次结构的数据拟合方差成份模型与线性回归模型的关系。方法 通过三类传统线性回归模型与两水平方差成份模型参数估计的对比,分析其内在联系。结果 线性回归模型参数估计以及估计的稳定性与自变量在水平2单位间和水平2单位内的变异大小有关,线性因归模型与方差成分模型参数估计及其稳定性的关系与水平2残差方差或单位内相关系数大小有关。结论 当数据具有层次结构特征时,三类线性回归模型均存在问题,方差成分模型可将线性回归模型的单一随机误差项分解到与数据层次结构相对应的各水平上,并估计水平2单位的随机效应。
Research into the relationship between the 2 level variance component model and the linear regression models.
, http://www.100md.com
Li Xiaosong,Ni Zongzan.
Department of Health Statistics,West China Universith of Medical Sciences(Chengdu 610041)
【Abstract】 Objective to explore the relationship between the variance component model and the linear regression models in fitting 2 level hierarchically-structured data.Methods by comparative analysis for the parameter estimates between three linear regression mdels and 2 level variance component moddel.Results the parameter estimates and it's stability of linear regression models is associated with the variation of explanatory variable between and within level 2units,and the relationship of parameter estimates and it's stability between linear regression models and variance component model is associated with level 2 residual variance or intatra-unit correlation.Conclusion the three linear regression models are inappropriate whten data are hierarchically structured,and both the single random error term of linear regression model can be decomposed into corresponding levels of hierarchical structure,and the randowm effects of level 2 units can be estimated by variance component model.
, 百拇医药
Key words hierachically-structured data variance component model linear regression models intra-unit correlation
多水平统计模型(multilevel statistical models)是英、美等发达国家教育学界80年代中后期发展起来的一门多元统计分析新技术,可有效处理传统多元统计方法难以分析的具有层次结构特征的数据(hierarchically structured data),是目前国际上统计学研究中一个新兴而重要的领域〔1〕。在临床医学,预防医学以及其它学科领域存在大量层次结构数据,因而多水平模型在这些领域具有广阔的应用前景。两水平方差成分模型是多水平模型中最基本的模型,而传统的线性回归模型仍是处理不具层次结构特征数据的有力工具。对两水平方差成分模型与各类传统线性回归模型之间内在联系的探讨,有助于对数据结构和多水平模型的认识和正确应用。
, http://www.100md.com
基本模型
现假定一具有两水平层次结构特征的数据,水平2单位为相应总体的随机样本。模型中有一个解释变量,yij、xij均为水平1变量,且β1在水平2单位间不存在变异。以符号Txx、Tyy、Txy分别表示x、y以及x与y的总的离均差平方和、积和;Axx、Ayy、Axy分别表示x、y以及x与y的水平2单位间离均差平方和、积和;Wxx、Wyy、Wxy分别表示x、y以及x与y的水平2单位内离均差平方和、积和。
对于上述数据,我们可建立以下四类模型:水平1的合并模型、水平2的聚集模型、水平2单位的固定效应模型以及两水平方差成份模型。
, 百拇医药 1.水平1的合并模型
以水平1单位为分析的基本单位,即将水平1单位合并在一起,忽略水平2单位对反应变量的效应。模型可表达为:
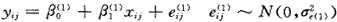
j=1,2,…,m示水平2单位,i=1,2,…,nj示水平1单位。括弧中的数字示模型编号,这里示模型1,以下同此。
根据最小二乘法原理,可得到模型参数及其方差的估计:
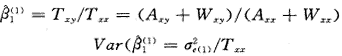
2.水平2的聚集模型
将水平1单位的特征包括反应变量和解释变量聚集为相应的水平2单位的特征,即计算各水平2单位所属的所有水平1单位的某种统计量如均数,以水平2单位为分析的基本单位。模型及其参数估计为:
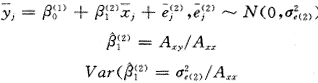
, http://www.100md.com
3.水平2单位的固定效应模型
对每个水平2单位拟合固定参数βoj,并假定一个普通的水平2单位内残差方差
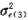 ,该模型拟合m条平行的回归线。模型及其参数估计为:
,该模型拟合m条平行的回归线。模型及其参数估计为: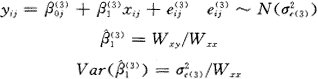
4.两水平方差成分模型
基本的模型结构与模型假设为:

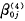 为随机变量,假定:
为随机变量,假定: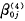 =
=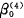 +u0j
+u0j, 百拇医药
代入式(4)有:yij=
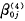 +
+ xij+u0j+eij
xij+u0j+eij这里,u0j亦为随机变量:
u0j~N(0,
 )
)水平1残差eij即线性回归模型中通常的残差项,eij~N(0,
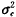 )。
)。, 百拇医药
与传统线性回归模型不同的是,两水平方差成分模型具有两个残差项,它属模型随机部分的结构。
固定参数的估计为:
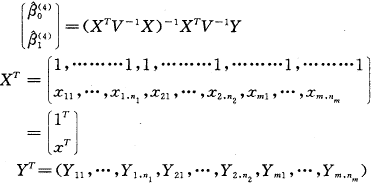
V为向量Y的协方差阵,这为分块对角阵,每个块对应于一个水平2单位:

根据线性代数原理,可得到V的逆阵为:
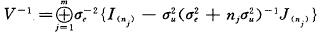
因此
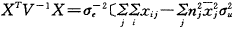
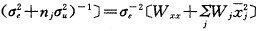
, 百拇医药
式中:
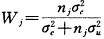
相似地:

因此:

式中,
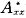 和
和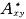 为加权的离均差平方和与积和,权重即为Wj。
为加权的离均差平方和与积和,权重即为Wj。讨 论
1.线性回归模型参数估计间的联系
, 百拇医药
现定义一指标
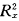 反映x在水平2单位间变异占总变异的比例,则
反映x在水平2单位间变异占总变异的比例,则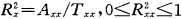 。进一步可导出:
。进一步可导出: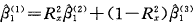 。可见。
。可见。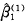 的估计介于
的估计介于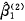 和
和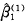 之间:如果Axx→0,那么
之间:如果Axx→0,那么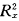 →0,
→0,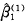 →
→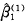 ,因Var(
,因Var(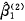 )=
)=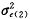 /Axx,故
/Axx,故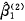 的估计不稳定;如果Wxx→0,那么
的估计不稳定;如果Wxx→0,那么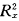 →1,
→1,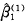 →
→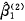 ,因Var(
,因Var(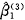 )=
)=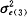 /Wxx,故
/Wxx,故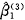 的估计不稳定。
的估计不稳定。, 百拇医药
2.两水平方差成分模型与线性回归模型参数估计的联系
由上述推导可见,两水平方差成分模型与传统线性回归模型参数估计的联系与区别关键在于权重Wj。
①如果
 =0,则Wj=nj,
=0,则Wj=nj,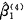 =
=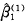 =Txy/Txx,Var(
=Txy/Txx,Var(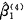 )=
)=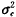 /Txx=Var(
/Txx=Var(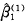 ),在这种情形下,水平2单位对反应变量无效应或效应相同,方差成分模型等价于水平1合并模型;如果
),在这种情形下,水平2单位对反应变量无效应或效应相同,方差成分模型等价于水平1合并模型;如果 相对于
相对于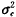 增加,则Wj趋近于0,
增加,则Wj趋近于0,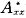 和
和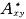 亦趋近于0,
亦趋近于0,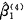 →
→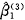 =WxyWxx,Var(
=WxyWxx,Var(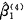 )→(
)→( +
+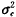 )/Wxx,在这种情形下,参数估计不依赖于水平2单位的间信息,方差成份模型的参数估计趋近于水平2单位固定效应模型;此外,从前面参数估计的表达式还可看出,水平2单位内的信息Wxx和Wxy对于模型固定参数的估计总是重要的。因此,未用到水平1单位信息的方法如水平2聚集模型在统计上是无效的(inefficient)〔1〕。
)/Wxx,在这种情形下,参数估计不依赖于水平2单位的间信息,方差成份模型的参数估计趋近于水平2单位固定效应模型;此外,从前面参数估计的表达式还可看出,水平2单位内的信息Wxx和Wxy对于模型固定参数的估计总是重要的。因此,未用到水平1单位信息的方法如水平2聚集模型在统计上是无效的(inefficient)〔1〕。, 百拇医药
②我们从另一个角度进一步考察这一问题。两水平方差成分模型反应变量的方差为:
Var(yij|β0,β1,xij)=Var(uoj+eij)=
 +
+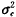
同一水平2单位所属的两个水平1单位(用i1,i2表示)间的协方差为:
Cov(u0j+ei1j,u0j+ei2j)=Cov(u0j,u0j)=

, 百拇医药
相关则为:
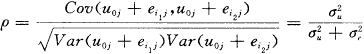
ρ即“单位内相关系数”(intra-unit correlation),反映了同一水平2单位内水平1单位的相似性或聚集性,测量了水平2单位间变异在总变异中所占的比例〔2〕。可以发现,Wj与ρ具有一定联系:
 =0,ρ=0,意味着数据不存在层次结构特征,此时Wj=nj;
=0,ρ=0,意味着数据不存在层次结构特征,此时Wj=nj; 相对于
相对于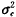 增加,ρ趋近于1,意味着数据层次结构特征明显,则Wj趋近于0,这与前面推论的情形是一致的。此外,一种极端的情形是,每个水平2单位中只有一个水平1单位即nj=1,此时仍可估计水平2残差方差
增加,ρ趋近于1,意味着数据层次结构特征明显,则Wj趋近于0,这与前面推论的情形是一致的。此外,一种极端的情形是,每个水平2单位中只有一个水平1单位即nj=1,此时仍可估计水平2残差方差 ,且ρ与Wj满足下式:ρ=(
,且ρ与Wj满足下式:ρ=( /σ2e)Wj,
/σ2e)Wj, /
/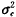 即方差成分比。
即方差成分比。, 百拇医药
如果数据具有层次结构特征,那么,除非x完全解释了y在水平2单位内的相似性或聚集性,否则y的残差相关,此时,三类线性回归模型都是不适宜的,且当残差存在复杂变异时,线性回归模型更难以探讨与之相关的因素。实际上,线性回归模型中单一的随机误差项包含了数据层次结构中高水平单位(如水平2单位)的随机效应与误差,多水平统计模型则将这种随机效应与误差分解到与数据层次结构相对的各水平上,并提供了拟合各水平复杂误差结构的可能性。
(致谢伦敦大学多水平模型课题组杨珉研究员提供的帮助)
参考文献
1.Goldstein,H.Multilevel Statistical Models.London:Edward Arnold.1995
2.杨珉.多元分析的发展——多水平模型简介.中国卫生统计.1994;11(5):32
, http://www.100md.com
中国微生态学杂志 2000年第5期第12卷 论 著
利用食品厂的废料发酵生产饲用微生物添加剂
作者:莫美华 林创华 冼毅和 邓宏益 谢秀菊
单位:莫美华 林创华 冼毅和 邓宏益(华南农业大学 食品系微生物教研室,广东广州510642);谢秀菊(广州市农科所,广东广州510308)
关键词:饲用微生物添加剂;发酵;啤酒糟.
中国微生态学杂志 2000年第5期第12卷 临床研究
联合应用回春生、促菌生治疗小儿迁延性肠炎疗效观察
作者:李凌媛 殷铮
单位:昆明市儿童医院, 云南 昆明650032
关键词:回春生;促菌生;迁延性肠炎., http://www.100md.com