应用余弦模型分析流行性腮腺炎发病季节性
作者:李艳梅 徐爽
单位:哈尔滨铁路中心卫生防疫站(150001)
关键词:
中国卫生统计990132 本文试用余弦模型分析法对哈尔滨铁路局1992~1996年度流行性腮腺炎发病季节特征进行分析。
资料与方法
将哈尔滨铁路局5年流行性腮腺炎发病资料按月合并,求出月平均发病率,并取其对数,每年按360°,每月各记为30°,并取每月15日为时点,用拟合余弦曲线分析有无季节变动及其变动规律模型。余弦曲线方程为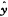 =
=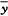 +Acos(t-
+Acos(t-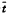 )
)
, http://www.100md.com
结果与分析
拟合结果见表1。
表1 哈尔滨铁路局1992~1996年流行性腮腺炎发病资料(1/10万)拟合余弦函数计算表 月份
(1)
t
(2)
y
(3)
lgy
(4)
lg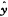 1
1
, 百拇医药
(5)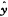 1
1
(6)
y-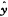 1
1
(7)=(3)-(6)
lg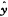 2
2
(8)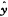 2
2
(9)
, http://www.100md.com
y-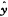 2
2
(10)=(3)-(9)
1
0
7.70
0.89
0.95
8.91
-1.21
0.93
8.5
, 百拇医药 -0.8
2
30
9.98
1.00
1.00
10.00
-0.02
1.04
10.96
-0.98
3
60
, 百拇医药
12.18
1.09
0.92
8.32
3.86
0.98
9.55
2.63
4
90
6.01
0.78
0.73
, http://www.100md.com
5.37
0.64
0.75
5.63
0.38
5
120
1.85
0.27
0.39
2.45
-0.60
0.35
, 百拇医药
2.24
-0.39
6
150
1.58
0.20
0.24
1.74
-0.16
0.18
1.52
0.06
7
, http://www.100md.com
180
1.71
0.23
0.07
1.17
-0.54
0.05
1.12
0.59
8
210
0.91
-0.04
, 百拇医药
0.02
1.05
-0.14
0.06
1.15
-0.24
9
240
1.17
0.07
0.10
1.26
-0.09
, 百拇医药
0.16
1.45
-0.28
10
270
2.08
0.32
0.29
1.95
0.13
0.31
2.05
0.03
, 百拇医药
11
300
4.45
0.65
0.54
3.47
0.98
0.50
3.16
1.29
12
330
4.28
, http://www.100md.com
0.63
0.78
6.03
-1.75
0.72
5.28
-1.00
合计
-
53.90
6.09
6.03
51.72
, 百拇医药
2.18
6.03
52.61
1.29
计算结果:
A1=0.4909,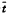 1=26.62°,
1=26.62°,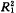 =0.87
=0.87
A2=0.0582,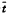 2=110.99°,
2=110.99°, =0.93
=0.93
, 百拇医药
由附表可见t=0°相当于1月15日,本文中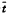 =26.62°,折算日期则相当于2月12日,即流行性腮腺炎发病高峰日,而26.62°+180°=206.62°,对应的日期是8月12日,为发病的低谷。
=26.62°,折算日期则相当于2月12日,即流行性腮腺炎发病高峰日,而26.62°+180°=206.62°,对应的日期是8月12日,为发病的低谷。
经方差分析,曲线关系成立(F=3.60,P<0.01)。
决定系数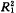 =0.87,说明月发病率的变异用余弦曲线拟合可减少87%,提示我局流行性腮腺炎发病的季节变动符合曲线模型,拟合结果见表1第(5)~(7)列。
=0.87,说明月发病率的变异用余弦曲线拟合可减少87%,提示我局流行性腮腺炎发病的季节变动符合曲线模型,拟合结果见表1第(5)~(7)列。
一般资料用第二谐量即可获得满意结果。本文应用简单余弦曲线拟合,从表第(7)列可看出,有的估计值与实际值相差较大,所以再运用含第二谐量的余弦三角多项式拟合,拟合方程为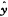 2=0.5075+0.4909cos(t-26.62°)+0.0582cos(2t-110.99°),求得
2=0.5075+0.4909cos(t-26.62°)+0.0582cos(2t-110.99°),求得 =0.93,拟合结果表明理论估计值与实际值之差明显减少,月发病率变异用含第二谐量三角多项式拟合减少93%,说明拟合优度有所改进。讨 论
=0.93,拟合结果表明理论估计值与实际值之差明显减少,月发病率变异用含第二谐量三角多项式拟合减少93%,说明拟合优度有所改进。讨 论
余弦模型可用于分析流行病学中昼时性与季节性资料。我局5年流行性腮腺炎发病有明显季节性,其变动符合余弦曲线模式。据此可估计最高月份发病率为10.96/10万,时间为2月,最低月份发病率为1.12/10万,月平均发病率为4.38/10万,与实际资料基本吻合。
2.用简单余弦模型拟合可使月发病率y的变异减少87%,用含第二谐量的三角多项式拟合,可使月发病率y的变异减少93%,拟合效果是满意的。由于我局地处中国北方地区,所以本文所得模型只适用于北方地区。
(本文承蒙哈尔滨医科大学蒋知俭老师指导,特表示感谢!), 百拇医药
单位:哈尔滨铁路中心卫生防疫站(150001)
关键词:
中国卫生统计990132 本文试用余弦模型分析法对哈尔滨铁路局1992~1996年度流行性腮腺炎发病季节特征进行分析。
资料与方法
将哈尔滨铁路局5年流行性腮腺炎发病资料按月合并,求出月平均发病率,并取其对数,每年按360°,每月各记为30°,并取每月15日为时点,用拟合余弦曲线分析有无季节变动及其变动规律模型。余弦曲线方程为
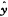 =
=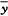 +Acos(t-
+Acos(t-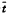 )
), http://www.100md.com
结果与分析
拟合结果见表1。
表1 哈尔滨铁路局1992~1996年流行性腮腺炎发病资料(1/10万)拟合余弦函数计算表 月份
(1)
t
(2)
y
(3)
lgy
(4)
lg
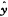 1
1, 百拇医药
(5)
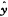 1
1(6)
y-
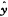 1
1(7)=(3)-(6)
lg
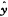 2
2(8)
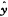 2
2(9)
, http://www.100md.com
y-
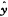 2
2(10)=(3)-(9)
1
0
7.70
0.89
0.95
8.91
-1.21
0.93
8.5
, 百拇医药 -0.8
2
30
9.98
1.00
1.00
10.00
-0.02
1.04
10.96
-0.98
3
60
, 百拇医药
12.18
1.09
0.92
8.32
3.86
0.98
9.55
2.63
4
90
6.01
0.78
0.73
, http://www.100md.com
5.37
0.64
0.75
5.63
0.38
5
120
1.85
0.27
0.39
2.45
-0.60
0.35
, 百拇医药
2.24
-0.39
6
150
1.58
0.20
0.24
1.74
-0.16
0.18
1.52
0.06
7
, http://www.100md.com
180
1.71
0.23
0.07
1.17
-0.54
0.05
1.12
0.59
8
210
0.91
-0.04
, 百拇医药
0.02
1.05
-0.14
0.06
1.15
-0.24
9
240
1.17
0.07
0.10
1.26
-0.09
, 百拇医药
0.16
1.45
-0.28
10
270
2.08
0.32
0.29
1.95
0.13
0.31
2.05
0.03
, 百拇医药
11
300
4.45
0.65
0.54
3.47
0.98
0.50
3.16
1.29
12
330
4.28
, http://www.100md.com
0.63
0.78
6.03
-1.75
0.72
5.28
-1.00
合计
-
53.90
6.09
6.03
51.72
, 百拇医药
2.18
6.03
52.61
1.29
计算结果:
A1=0.4909,
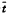 1=26.62°,
1=26.62°,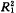 =0.87
=0.87A2=0.0582,
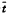 2=110.99°,
2=110.99°, =0.93
=0.93, 百拇医药
由附表可见t=0°相当于1月15日,本文中
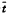 =26.62°,折算日期则相当于2月12日,即流行性腮腺炎发病高峰日,而26.62°+180°=206.62°,对应的日期是8月12日,为发病的低谷。
=26.62°,折算日期则相当于2月12日,即流行性腮腺炎发病高峰日,而26.62°+180°=206.62°,对应的日期是8月12日,为发病的低谷。经方差分析,曲线关系成立(F=3.60,P<0.01)。
决定系数
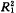 =0.87,说明月发病率的变异用余弦曲线拟合可减少87%,提示我局流行性腮腺炎发病的季节变动符合曲线模型,拟合结果见表1第(5)~(7)列。
=0.87,说明月发病率的变异用余弦曲线拟合可减少87%,提示我局流行性腮腺炎发病的季节变动符合曲线模型,拟合结果见表1第(5)~(7)列。一般资料用第二谐量即可获得满意结果。本文应用简单余弦曲线拟合,从表第(7)列可看出,有的估计值与实际值相差较大,所以再运用含第二谐量的余弦三角多项式拟合,拟合方程为
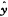 2=0.5075+0.4909cos(t-26.62°)+0.0582cos(2t-110.99°),求得
2=0.5075+0.4909cos(t-26.62°)+0.0582cos(2t-110.99°),求得 =0.93,拟合结果表明理论估计值与实际值之差明显减少,月发病率变异用含第二谐量三角多项式拟合减少93%,说明拟合优度有所改进。讨 论
=0.93,拟合结果表明理论估计值与实际值之差明显减少,月发病率变异用含第二谐量三角多项式拟合减少93%,说明拟合优度有所改进。讨 论余弦模型可用于分析流行病学中昼时性与季节性资料。我局5年流行性腮腺炎发病有明显季节性,其变动符合余弦曲线模式。据此可估计最高月份发病率为10.96/10万,时间为2月,最低月份发病率为1.12/10万,月平均发病率为4.38/10万,与实际资料基本吻合。
2.用简单余弦模型拟合可使月发病率y的变异减少87%,用含第二谐量的三角多项式拟合,可使月发病率y的变异减少93%,拟合效果是满意的。由于我局地处中国北方地区,所以本文所得模型只适用于北方地区。
(本文承蒙哈尔滨医科大学蒋知俭老师指导,特表示感谢!), 百拇医药