单侧检验辨释
作者：陆守曾
单位：南通医学院(226001)
关键词：
中国卫生统计990220 在假设检验中选用单侧检验，主要是为了提高检验效率，即提高(1-β)。本文就单侧检验的意义，单、双侧检验的假设与分布中的单、双尾面积，以及单侧检验之应用价值等问题进行探讨；此外，亦述及只有单侧检验的方法。
单侧检验的一般意义
当所设H0为总体参数等于某一定值，而H1为仅从一个方向上偏离此定值者，为单侧检验。以下是几种常见的单侧检验，注意与相应的双侧检验分辨。
1.检验两组的差异显著性时，只考虑A>B之意义，不考虑AB和A
2.检验差值均数的显著性时，只考虑正值的意义，不考虑负值之可能性者，为单侧检验(若上述正值和负值之设置相反，亦为单侧检验)；同时考虑包含正值和负值两个方面的可能性者，为双侧检验。例如，试验某药是否有降血脂作用，一般应取双侧检验；而对伤口之愈合试用某辅助疗法时，由于即使不采用任何治疗方法伤口亦大多可自愈，故具备了选用单侧检验的条件。
3.检验相关的显著性时，只考虑正相关的意义，不考虑负相关的可能性者，为单侧检验(若上述正相关和负相关之设置相反，亦为单侧检验)；同时考虑正相关和负相关两个可能性者，为双侧检验。回归亦然。例如，两种试剂同时应用时可能有交互作用，但不明确作用之正负，即产生协同作用抑拮抗作用，一般应采用双侧检验；如果有理由只考虑其中之一(设为协同作用)而不必考虑另一作用(为拮抗作用)出现之可能性时，可以选用单侧检验。
4.为检验多个实验组与一个对照组之差异而进行多重比较时，只考虑在一个方向上的差异，不考虑在另一方向上出现差异之可能性者，为单侧检验；同时考虑包含两个相反方向上差异之可能性者，为双侧检验。例如，3个实验组T1、T2、T3与同一个对照组C比较的4组设计中，无疑H0：T1=C，T2=C，T3=C；然而H1却有以下两种状态：
, 百拇医药
单侧检验 T1>C，T2>C，T3>C(出现其中1个或2个或全部)
双侧检验 T1≠C，T2≠C，T3≠C(出现其中1个或2个或全部)
上述单侧检验的H1也可以是T123”和“<”。
对于大多数假设检验方法，实际应用时都要依据资料之性质及样本之特征注意辨识是否适宜采用单侧检验；如不适宜，则采用双侧检验。
单、双侧检验与单、双尾面积
假设检验的单侧、双侧与检验中涉及的单尾、双尾，它们既有密切的联系，又有不同的涵义，尤其要注意它们之间在各方法中固有的对应关系。
, 百拇医药
1.一个误解：单侧检验就是“单尾检验”(双侧检验就是“双尾检验”)。为易于解释，单侧检验常通过t检验法举例说明。在t-分布图形上，单侧检验的P值与单尾面积相符，于是，“ONE-SIDED”与“ONE-TAILED”亦被混用；由此导致将假设检验中单侧的意义与特定分布曲线下的单尾面积视同一体，甚至说成“单尾检验”，这是对单侧检验的错误理解。其实，单侧检验与单尾面积符合一致的情况只存在于某些方法：如u检验法、t检验法(分布对称)、两组秩和检验法、四格表确切概率检验法(分布不对称，唯当n1=n2时对称)，并非广泛存在。
2.另一种相符：双侧检验与单尾面积。在F-分布中，用于检验均数间差异的方差分析，由于被检验的各个均数是无序排列的，故必然是双侧检验；其P值对应于F-分布曲线下界值右端的尾部，故必然是单尾面积。设两个样本的含量为n1=12和n2=10，在F-分布界值表上和t-分布界值表上可分别查出以下的双侧检验界值，两者并有如下关系：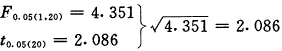
, 百拇医药
再设两样本含量相当大时，亦可在F-分布界值表上和正态分布界值表上分别查出以下的双侧检验界值，两者同样有如下关系：
上列两组界值均明确表达了属于双侧检验的对应关系，而其中方差分析的P值(0.05)却与F-分布曲线下界值右端面积相符，即双侧检验在此恰与单尾面积相符。
此外，χ2检验属双侧检验(无序排列)，其P值对应于χ2分布曲线下界值右端的面积，亦是双侧检验与单尾面积的相符。
3.一个被忽视的问题：方差齐性检验与特殊的“双尾”面积。设两个样本方差如下，并按相反的两种顺序分别计算F值(取α=0.05)：
, http://www.100md.com
右尾界值 F0.025(15，10)=3.522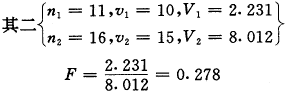
左尾界值 F0.025(10，15)=0.284
这里的P值是F(15，10)分布曲线下界值的右尾面积与F(10，15)分布曲线下界值的左尾面积之和，即
故结果为方差不齐，见图1。至于两个方差按相反位置计算的两个F值，以及两个自由度按相反组合查出的两个F界值，显然均存在倒数关系：1/3.591=0.278，1/3.522=0.284。可见，“双尾”在此非但不对称，而且分属于两条不同的F-分布曲线，是十分明确的了。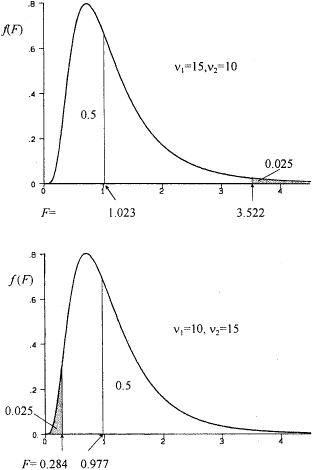
, 百拇医药
图1 方差齐性检验中与F值对应的“双尾”面积
一般用于方差齐性检验的F界值表，往往直接将右端单尾F0.025作为F0.05界值，如本小节例子可得如下数值：
(1)单尾面积(右)： P=0.10 0.05 0.025 0.01 …
(2)2×(1)： P=0.20 0.10 0.05 0.02 …
(3)方差齐性检验界值： F=2.244 2.845 3.522 4.558 …
在F-分布曲线下，当F=1时，其左、右面积有如下关系：
当v1=v2，左面积=右面积，方差齐性检验界值准确；
, 百拇医药
当v1>v2，左面积<右面积，方差齐性检验界值近似；
当v12，左面积>右面积，方差齐性检验界值近似。
4.单侧检验的辨识：备择假设。单侧检验的备择假设，是仅限于从某一确定的方向上偏离无效假设。如：
可见，单侧检验之结论，必须依据已经确认的备择假设所规范者，即
P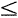
α，拒绝H0，同时接受H1；
P>α，不拒绝H0。
, 百拇医药
至于此处α值究竟是某分布的单尾面积或双尾面积或其他形式的组合，却与结论无直接关系。有的书刊上将ONE-SIDED与ONE-TAILED混淆，应注意纠正。
只有单侧检验的方法
一组按时间顺序，空间顺序或其他顺序收集的数据，当然是有序的。为检验其序列是否具有某种方向上的趋势；如升、降、曲线等，只要散点图分布的“轴”明显偏离其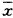
轴者，可通过均方递差检验(Mean square successive difference test)〔1〕进行分析。计算公式如下：
H0∶C=0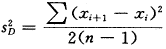
, http://www.100md.com
H1∶C>0
α=0.05
C为均方递差检验的统计量；
为递差均方；s2为均方。如数据序列是随机的，即无任何方向上的趋势时，为s2的估计值，总体C=0；如数据序列具有某方向上的趋势时，则相邻变量值之间的变异程度将小于各变量值与均数之间的变异程度，故将出现2，C>0。当达到C≥C0.05时，Pα，可作拒绝H0而接受H1之结论。
, 百拇医药
此法用于检验数据序列是否存在某种方向趋势时，其统计量C值在0～1，若C=0，必然=s2，表示总体数列只有随机变异，而无任何方向上的趋势。至于另一侧C<0的意义，如变异之幅度随序列延续而扩大时可能出现，这是相关分布的偏性所致，而与检验方向趋势无关，应不予考虑。故均方递差检验只能是单侧检验，其H1：C>0。
当n超出工具表〔1〕所列范围时，C分布将近似正态，可由下式转换为u值，而uα亦必须取单尾面积作为单侧检验的界值。
此外，某些非参数检验亦属只有单侧检验的方法。
单侧检验的应用价值
, 百拇医药
1.正确采用单侧检验，理论上将获得高于双侧检验的效率。要对假设检验的不同方法或同一方法的不同应用方式作出评价，最终应以检验效率的高低为准。这个“效率”就是探察出真实H1之能力，亦称功效或把握度，其概率为(1-β)〔2〕。从图2可见，在设定的H0和H1条件下，用单侧检验时的(1-β)值明显大于双侧检验，亦即前者的把握度大于后者。
图2 在H0和H1不变时，用单侧检验和
双侧检验的“1-β”面积
把握度的值(1-β)随H0和H1两个总体的参数之间距而变动：间距越大，(1-β)亦越大，反之越小，并形成把握度曲线，称OC曲线(Operating characteristic curve)。从图3可见，在设定的总体参数条件下，采用单侧检验时的OC曲线始终位于双侧检验时的OC曲线之上，即前者的(1-β)值始终高于后者，至于高出的幅度，则以(1-β)=β=0.5为上限。若越过这个极限，原来的(1-β)将与β“对换”，因为显然不应该出现(1-β)<β，否则此假设检验将无实际应用意义。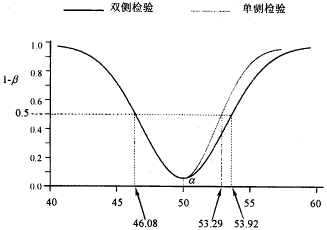
, 百拇医药
图3 把握度曲线(OC曲线)设u0=50，σ=10,n=25
综合图2、图3所示，可得结论：正确采用单侧检验将获得高于双侧检验之效率。
2.对“与其把概率因子估计得太少，不如估计得太多要妥当些”之评论。如果正确地按照同一个α水准进行假设检验，并不存在单侧检验与双侧检验所得概率孰多孰少的问题。所谓“双侧检验较为妥当”的说法，仅在以下情况有意义：按原资料之性质，对原本只适用双侧检验者误用了单侧检验。下面是一个u值双侧检验的例子，已算得u=1.88，用双侧检验：α=0.05，uα=1.96，P>α(P=0.06)；
用单侧检验：α=0.05，uα=1.64，P<α(P=0.03)。
在此，用双侧检验是正确的，应得P>α；用单侧检验是错误的，不应得P<α。可见并非因为选用单侧检验或双侧检验而导致对概率值估计是否准确的问题。
, 百拇医药
3.从严掌握选用单侧检验的条件。上述u检验的例子提示：当出现如下情况时，对同一资料采用单侧检验抑双侧检验，将得到不同的检验结果：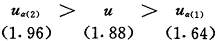
因此，必须审慎地根据资料性质并考察样本数据特征，对照所设备择假设H1的具体内容，确定是否采用单侧检验。若应该用双侧检验而误用单侧检验，将可能导致假阳性结果；若本可以用单侧检验却仍采取双侧检验，则可能导致假阴性结果，亦即失去了做出正确分辨的机会。后者无疑也是一种失误，且往往不易被识破!笔者认为：对于单侧检验的选用既要从严掌握，又要在条件已具备时毅然运用，两者皆不可偏废。
(本文承陈峰博士、陈佩珍副教授协助完成，特此致谢!)
作者单位：
参考文献
1.杨树勤主编.中国医学百科全书.医学统计学.第1版.上海：上海科学技术出版社，1985，115
2.郭祖超主编.医用数理统计方法.第3版.北京：人民卫生出版社，1988，108, 百拇医药
单位：南通医学院(226001)
关键词：
中国卫生统计990220 在假设检验中选用单侧检验，主要是为了提高检验效率，即提高(1-β)。本文就单侧检验的意义，单、双侧检验的假设与分布中的单、双尾面积，以及单侧检验之应用价值等问题进行探讨；此外，亦述及只有单侧检验的方法。
单侧检验的一般意义
当所设H0为总体参数等于某一定值，而H1为仅从一个方向上偏离此定值者，为单侧检验。以下是几种常见的单侧检验，注意与相应的双侧检验分辨。
1.检验两组的差异显著性时，只考虑A>B之意义，不考虑A
2.检验差值均数的显著性时，只考虑正值的意义，不考虑负值之可能性者，为单侧检验(若上述正值和负值之设置相反，亦为单侧检验)；同时考虑包含正值和负值两个方面的可能性者，为双侧检验。例如，试验某药是否有降血脂作用，一般应取双侧检验；而对伤口之愈合试用某辅助疗法时，由于即使不采用任何治疗方法伤口亦大多可自愈，故具备了选用单侧检验的条件。
3.检验相关的显著性时，只考虑正相关的意义，不考虑负相关的可能性者，为单侧检验(若上述正相关和负相关之设置相反，亦为单侧检验)；同时考虑正相关和负相关两个可能性者，为双侧检验。回归亦然。例如，两种试剂同时应用时可能有交互作用，但不明确作用之正负，即产生协同作用抑拮抗作用，一般应采用双侧检验；如果有理由只考虑其中之一(设为协同作用)而不必考虑另一作用(为拮抗作用)出现之可能性时，可以选用单侧检验。
4.为检验多个实验组与一个对照组之差异而进行多重比较时，只考虑在一个方向上的差异，不考虑在另一方向上出现差异之可能性者，为单侧检验；同时考虑包含两个相反方向上差异之可能性者，为双侧检验。例如，3个实验组T1、T2、T3与同一个对照组C比较的4组设计中，无疑H0：T1=C，T2=C，T3=C；然而H1却有以下两种状态：
, 百拇医药
单侧检验 T1>C，T2>C，T3>C(出现其中1个或2个或全部)
双侧检验 T1≠C，T2≠C，T3≠C(出现其中1个或2个或全部)
上述单侧检验的H1也可以是T1
对于大多数假设检验方法，实际应用时都要依据资料之性质及样本之特征注意辨识是否适宜采用单侧检验；如不适宜，则采用双侧检验。
单、双侧检验与单、双尾面积
假设检验的单侧、双侧与检验中涉及的单尾、双尾，它们既有密切的联系，又有不同的涵义，尤其要注意它们之间在各方法中固有的对应关系。
, 百拇医药
1.一个误解：单侧检验就是“单尾检验”(双侧检验就是“双尾检验”)。为易于解释，单侧检验常通过t检验法举例说明。在t-分布图形上，单侧检验的P值与单尾面积相符，于是，“ONE-SIDED”与“ONE-TAILED”亦被混用；由此导致将假设检验中单侧的意义与特定分布曲线下的单尾面积视同一体，甚至说成“单尾检验”，这是对单侧检验的错误理解。其实，单侧检验与单尾面积符合一致的情况只存在于某些方法：如u检验法、t检验法(分布对称)、两组秩和检验法、四格表确切概率检验法(分布不对称，唯当n1=n2时对称)，并非广泛存在。
2.另一种相符：双侧检验与单尾面积。在F-分布中，用于检验均数间差异的方差分析，由于被检验的各个均数是无序排列的，故必然是双侧检验；其P值对应于F-分布曲线下界值右端的尾部，故必然是单尾面积。设两个样本的含量为n1=12和n2=10，在F-分布界值表上和t-分布界值表上可分别查出以下的双侧检验界值，两者并有如下关系：
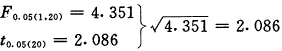
, 百拇医药
再设两样本含量相当大时，亦可在F-分布界值表上和正态分布界值表上分别查出以下的双侧检验界值，两者同样有如下关系：
上列两组界值均明确表达了属于双侧检验的对应关系，而其中方差分析的P值(0.05)却与F-分布曲线下界值右端面积相符，即双侧检验在此恰与单尾面积相符。
此外，χ2检验属双侧检验(无序排列)，其P值对应于χ2分布曲线下界值右端的面积，亦是双侧检验与单尾面积的相符。
3.一个被忽视的问题：方差齐性检验与特殊的“双尾”面积。设两个样本方差如下，并按相反的两种顺序分别计算F值(取α=0.05)：
, http://www.100md.com
右尾界值 F0.025(15，10)=3.522
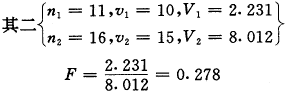
左尾界值 F0.025(10，15)=0.284
这里的P值是F(15，10)分布曲线下界值的右尾面积与F(10，15)分布曲线下界值的左尾面积之和，即
故结果为方差不齐，见图1。至于两个方差按相反位置计算的两个F值，以及两个自由度按相反组合查出的两个F界值，显然均存在倒数关系：1/3.591=0.278，1/3.522=0.284。可见，“双尾”在此非但不对称，而且分属于两条不同的F-分布曲线，是十分明确的了。
, 百拇医药
图1 方差齐性检验中与F值对应的“双尾”面积
一般用于方差齐性检验的F界值表，往往直接将右端单尾F0.025作为F0.05界值，如本小节例子可得如下数值：
(1)单尾面积(右)： P=0.10 0.05 0.025 0.01 …
(2)2×(1)： P=0.20 0.10 0.05 0.02 …
(3)方差齐性检验界值： F=2.244 2.845 3.522 4.558 …
在F-分布曲线下，当F=1时，其左、右面积有如下关系：
当v1=v2，左面积=右面积，方差齐性检验界值准确；
, 百拇医药
当v1>v2，左面积<右面积，方差齐性检验界值近似；
当v1
4.单侧检验的辨识：备择假设。单侧检验的备择假设，是仅限于从某一确定的方向上偏离无效假设。如：
可见，单侧检验之结论，必须依据已经确认的备择假设所规范者，即
P
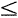α，拒绝H0，同时接受H1；P>α，不拒绝H0。
, 百拇医药
至于此处α值究竟是某分布的单尾面积或双尾面积或其他形式的组合，却与结论无直接关系。有的书刊上将ONE-SIDED与ONE-TAILED混淆，应注意纠正。
只有单侧检验的方法
一组按时间顺序，空间顺序或其他顺序收集的数据，当然是有序的。为检验其序列是否具有某种方向上的趋势；如升、降、曲线等，只要散点图分布的“轴”明显偏离其
轴者，可通过均方递差检验(Mean square successive difference test)〔1〕进行分析。计算公式如下：H0∶C=0
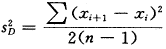
, http://www.100md.com
H1∶C>0
α=0.05
C为均方递差检验的统计量；
为递差均方；s2为均方。如数据序列是随机的，即无任何方向上的趋势时，为s2的估计值，总体C=0；如数据序列具有某方向上的趋势时，则相邻变量值之间的变异程度将小于各变量值与均数之间的变异程度，故将出现, 百拇医药
此法用于检验数据序列是否存在某种方向趋势时，其统计量C值在0～1，若C=0，必然
=s2，表示总体数列只有随机变异，而无任何方向上的趋势。至于另一侧C<0的意义，如变异之幅度随序列延续而扩大时可能出现，这是相关分布的偏性所致，而与检验方向趋势无关，应不予考虑。故均方递差检验只能是单侧检验，其H1：C>0。当n超出工具表〔1〕所列范围时，C分布将近似正态，可由下式转换为u值，而uα亦必须取单尾面积作为单侧检验的界值。
此外，某些非参数检验亦属只有单侧检验的方法。
单侧检验的应用价值
, 百拇医药
1.正确采用单侧检验，理论上将获得高于双侧检验的效率。要对假设检验的不同方法或同一方法的不同应用方式作出评价，最终应以检验效率的高低为准。这个“效率”就是探察出真实H1之能力，亦称功效或把握度，其概率为(1-β)〔2〕。从图2可见，在设定的H0和H1条件下，用单侧检验时的(1-β)值明显大于双侧检验，亦即前者的把握度大于后者。
图2 在H0和H1不变时，用单侧检验和
双侧检验的“1-β”面积
把握度的值(1-β)随H0和H1两个总体的参数之间距而变动：间距越大，(1-β)亦越大，反之越小，并形成把握度曲线，称OC曲线(Operating characteristic curve)。从图3可见，在设定的总体参数条件下，采用单侧检验时的OC曲线始终位于双侧检验时的OC曲线之上，即前者的(1-β)值始终高于后者，至于高出的幅度，则以(1-β)=β=0.5为上限。若越过这个极限，原来的(1-β)将与β“对换”，因为显然不应该出现(1-β)<β，否则此假设检验将无实际应用意义。
, 百拇医药
图3 把握度曲线(OC曲线)设u0=50，σ=10,n=25
综合图2、图3所示，可得结论：正确采用单侧检验将获得高于双侧检验之效率。
2.对“与其把概率因子估计得太少，不如估计得太多要妥当些”之评论。如果正确地按照同一个α水准进行假设检验，并不存在单侧检验与双侧检验所得概率孰多孰少的问题。所谓“双侧检验较为妥当”的说法，仅在以下情况有意义：按原资料之性质，对原本只适用双侧检验者误用了单侧检验。下面是一个u值双侧检验的例子，已算得u=1.88，用双侧检验：α=0.05，uα=1.96，P>α(P=0.06)；
用单侧检验：α=0.05，uα=1.64，P<α(P=0.03)。
在此，用双侧检验是正确的，应得P>α；用单侧检验是错误的，不应得P<α。可见并非因为选用单侧检验或双侧检验而导致对概率值估计是否准确的问题。
, 百拇医药
3.从严掌握选用单侧检验的条件。上述u检验的例子提示：当出现如下情况时，对同一资料采用单侧检验抑双侧检验，将得到不同的检验结果：
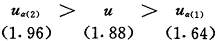
因此，必须审慎地根据资料性质并考察样本数据特征，对照所设备择假设H1的具体内容，确定是否采用单侧检验。若应该用双侧检验而误用单侧检验，将可能导致假阳性结果；若本可以用单侧检验却仍采取双侧检验，则可能导致假阴性结果，亦即失去了做出正确分辨的机会。后者无疑也是一种失误，且往往不易被识破!笔者认为：对于单侧检验的选用既要从严掌握，又要在条件已具备时毅然运用，两者皆不可偏废。
(本文承陈峰博士、陈佩珍副教授协助完成，特此致谢!)
作者单位：
参考文献
1.杨树勤主编.中国医学百科全书.医学统计学.第1版.上海：上海科学技术出版社，1985，115
2.郭祖超主编.医用数理统计方法.第3版.北京：人民卫生出版社，1988，108, 百拇医药