对应分析方法在学生体质调研样品分类中的应用
作者:梁荣辉 张科 刘若群
单位:梁荣辉 河北师范大学(050016); 张科 刘若群河北省教委体卫处
关键词:
中国卫生统计990211 学生体质调研中样品(即学生个体)分类问题的研究,一直为人们所关注。以前所引用的Q型聚类分析、Q型因子分析等方法,一般只是处理一些小样本的问题,真正用于大样本的不多,而体质调研中的问题大多是大样本,因此实用性较差。事实上,多元统计分析中的对应分析方法不受上述限制,可以用于对大样本样品的分类;此外,在对样品分类的同时,还可以对指标进行分类、分析各指标的重要程度以及样品与指标的关系。鉴此,本文将该方法引入学生体质调研样品分类问题中,并且辅以求最短距离等方法,较好地解决了样品分类的问题。
资料与方法
对应分析方法是将R型因子分析与Q型因子分析相结合、对指标与样品同时进行分类的一种多元统计分析方法。计算时,首先得到R型因子分析的结果,然后据其得到Q型因子分析的结果,因此,克服了大样本时计算上的困难。
, http://www.100md.com
1.计算数据变换矩阵Z
设有n个样品,p个指标x1,x2,…,xp,数据记为xij。
对数据xij进行对应变换,得到:Z=[zij]n×p,其中,
2.进行R型因子分析
计算矩阵Z′Z的特征值:λ1≥λ2≥…≥λp。
根据累积贡献率80%、85%或90%,取前m个特征值,计算相应的单位特征向量,从而得到R型因子载荷矩阵;在两两因子轴平面上作出指标散点图。
, 百拇医药
3.进行Q型因子分析
对上面计算出的m个特征值,计算矩阵ZZ′的单位特征向量,从而得到Q型因子载荷矩阵;在与R型相应的因子平面上作出样品散点图。
4.合理进行解释与推断
根据对应分析的原理、方法,针对不同的实际问题,进行合理地解释、分析。
5.1995年全国体质调研河北省城市22岁年龄组男生250人,9项指标:x1,肺活量;x2,身高;x3,体重;x4,胸围;x5,50米;x6,立定跳远;x7,引体向上;x8,1 000米;x9,立位体前屈。
结果与分析
, 百拇医药
1.计算特征值与因子载荷
对原始数据进行变换,得到矩阵Z,计算矩阵Z的特征值,见表1。
表1 特征值与贡献率 序
特征值
贡献率(%)
累积贡献率(%)
1
0.0031095
70.53
70.53
2
0.0005061
, 百拇医药
11.48
82.01
3
0.0003398
7.71
89.72
4
0.0003541
5.76
95.48
5
0.0001252
2.84
, 百拇医药
98.32
6
0.0000485
1.10
99.42
7
0.0000203
0.46
99.88
8
0.0000052
0.12
100.00
, 百拇医药
9
0.0000000
0.00
100.00
前4个特征值的累积贡献率达到95.48%,故取4个特征值,相应地得到R型因子分析与Q型因子分析载荷矩阵。
2.Q型因子分析
(1)分类 根据所取特征值与特征向量的个数,可在平面、空间或两两平面上绘制散点图,进而将样品分类。本研究共取了4个因子,先取前两个因子在平面上绘制散点图,但由于样品较多,不易定界分类。通过对有关文献与本研究的图形分类进行剖析,其结果实质上是以第一因子载荷为主,第二因子载荷为辅,因此,我们采取以第一因子载荷为主、第二因子载荷为辅、参考第三、四因子载荷的分类方法,将样品按5个等级分类,根据一般的分类等级分为上等、中上等、中等、中下等与下等,比重分别为10%、20%、40%、20%、10%。
, 百拇医药
将Q型第一因子载荷值从大到小排序,前25名被评为上等;26~75名被评为中上等;76~175名被评为中等;176~225名被评为中下等;最后25名被评为下等。各类的平均数、总平均数与标准差见表2。 表2 各类的平均数 等级
指标
x1
x2
x3
x4
x5
x6
x7
, http://www.100md.com
x8
x9
250人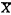
4211.43
170.40
61.48
86.38
7.49
237.57
7.66
239.48
, 百拇医药
14.86
s
659.23
5.86
6.15
4.06
0.43
15.91
3.41
22.39
5.58
上 等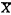
, http://www.100md.com
5310.00
175.36
66.47
88.94
7.44
240.76
6.88
233.34
15.17
中上等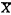
4743.00
, 百拇医药 172.37
62.22
87.35
7.44
241.54
7.42
239.31
15.43
中 等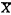
4205.00
170.43
61.78
, 百拇医药
86.79
7.44
237.91
7.60
237.21
14.94
中下等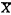
3703.00
168.10
60.01
84.95
, 百拇医药 7.64
234.84
7.48
242.94
14.25
下 等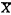
3091.00
165.95
56.70
83.06
7.58
230.56
, 百拇医药
9.56
248.12
14.30
上等(剔70)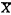
5298.00
175.42
66.60
88.85
7.44
240.54
6.75
, 百拇医药 234.20
15.29
中等(剔70)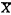
4277.00
171.09
61.30
86.19
7.49
238.57
7.65
236.48
, 百拇医药 14.92
70号样品
5600.00
173.90
63.30
91.00
7.50
246.00
10.0
212.70
12.20
将Q型第二因子载荷值从大到小排序,找出与上述分类结果不一致的样品。
, 百拇医药
(2)分类不一致的样品的处理 样品70号在第一次分类中分为上等,在第二次分类中分为中等,应该分在哪个等级呢?这里采用求最短距离与用相似系数判断的方法,距离公式为: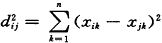
相似系数取两个样品的相关系数。
分别计算除去70号样品的两类的平均数,见表2中的上等(剔70)与中等(剔70)行。为了消除量纲对计算结果的影响,分别将该样品与剔除其上等、中等的指标进行标准化处理。用处理后的值计算该样品与它们的距离、相关系数。与上等类的距离为3.12、相关系数为0.99998;与中等类的距离为7.83、相关系数为0.99983,故将该样品归入上等类。对其他分类不一致的样品进行同样的处理。
同理,可对Q型第三、四因子载荷值从大到小排序,用上述同样的方法判别归类。
, 百拇医药
经过以上重新归类,5个等级的人数有所变化,分别为29、52、94、49、26,所占的比重分别为:11.6%、20.8%、37.6%、19.6%、10.4%。调整归类后的比重有较大变化时,应参考第一因子的分类。
3.R型因子分析
(1)分类 取R型因子分析的前两个因子在平面上绘制散点图,肺活量指标在平面的左侧,与上等类样品在一个类区;其余指标均在右侧,与下等类样品在一个类区。散点较分散,指标之间的分类趋势不明显。
(2)指标的重要性分析 由R型因子分析载荷矩阵的第一因子载荷知,指标肺活量、身高、立定跳远与1 000米的绝对值较大,因此,可以认为是相对重要的指标,事实上,它们是不同类指标的代表。
小 结
1.本文利用对应分析方法,解决了体质调研中大样本样品分类的问题,当根据几个因子载荷值的分类不一致时,可用两点间距离公式或相似系数等方法进行调整。同时也能对指标进行分类、对指标的重要性进行分析以及研究与样品的关系,因此,有一定的实用价值。
, 百拇医药
2.本文的计算量较大,可编制程序进行计算,对计算机内存等方面的要求也不高,具有一定的可行性;本文的研究除了对所研究对象进行分类外,还可利用该结果对所属总体的其他样本进行分类,具有一定的通用性。
参考文献
1.林少宫.多元统计分析及计算程序.武汉:华中工学院出版社,1987.,229~246
2.成都地质学院.《概率论与数理统计》编写小组.《概率论与数理统计》.北京:地质出版社,1981,367~382
3.中国学生体质与健康研究组,95中国学生体质与健康调查研报告.长春:吉林科学技术出版社,1996, http://www.100md.com
单位:梁荣辉 河北师范大学(050016); 张科 刘若群河北省教委体卫处
关键词:
中国卫生统计990211 学生体质调研中样品(即学生个体)分类问题的研究,一直为人们所关注。以前所引用的Q型聚类分析、Q型因子分析等方法,一般只是处理一些小样本的问题,真正用于大样本的不多,而体质调研中的问题大多是大样本,因此实用性较差。事实上,多元统计分析中的对应分析方法不受上述限制,可以用于对大样本样品的分类;此外,在对样品分类的同时,还可以对指标进行分类、分析各指标的重要程度以及样品与指标的关系。鉴此,本文将该方法引入学生体质调研样品分类问题中,并且辅以求最短距离等方法,较好地解决了样品分类的问题。
资料与方法
对应分析方法是将R型因子分析与Q型因子分析相结合、对指标与样品同时进行分类的一种多元统计分析方法。计算时,首先得到R型因子分析的结果,然后据其得到Q型因子分析的结果,因此,克服了大样本时计算上的困难。
, http://www.100md.com
1.计算数据变换矩阵Z
设有n个样品,p个指标x1,x2,…,xp,数据记为xij。
对数据xij进行对应变换,得到:Z=[zij]n×p,其中,

2.进行R型因子分析
计算矩阵Z′Z的特征值:λ1≥λ2≥…≥λp。
根据累积贡献率80%、85%或90%,取前m个特征值,计算相应的单位特征向量,从而得到R型因子载荷矩阵;在两两因子轴平面上作出指标散点图。
, 百拇医药
3.进行Q型因子分析
对上面计算出的m个特征值,计算矩阵ZZ′的单位特征向量,从而得到Q型因子载荷矩阵;在与R型相应的因子平面上作出样品散点图。
4.合理进行解释与推断
根据对应分析的原理、方法,针对不同的实际问题,进行合理地解释、分析。
5.1995年全国体质调研河北省城市22岁年龄组男生250人,9项指标:x1,肺活量;x2,身高;x3,体重;x4,胸围;x5,50米;x6,立定跳远;x7,引体向上;x8,1 000米;x9,立位体前屈。
结果与分析
, 百拇医药
1.计算特征值与因子载荷
对原始数据进行变换,得到矩阵Z,计算矩阵Z的特征值,见表1。
表1 特征值与贡献率 序
特征值
贡献率(%)
累积贡献率(%)
1
0.0031095
70.53
70.53
2
0.0005061
, 百拇医药
11.48
82.01
3
0.0003398
7.71
89.72
4
0.0003541
5.76
95.48
5
0.0001252
2.84
, 百拇医药
98.32
6
0.0000485
1.10
99.42
7
0.0000203
0.46
99.88
8
0.0000052
0.12
100.00
, 百拇医药
9
0.0000000
0.00
100.00
前4个特征值的累积贡献率达到95.48%,故取4个特征值,相应地得到R型因子分析与Q型因子分析载荷矩阵。
2.Q型因子分析
(1)分类 根据所取特征值与特征向量的个数,可在平面、空间或两两平面上绘制散点图,进而将样品分类。本研究共取了4个因子,先取前两个因子在平面上绘制散点图,但由于样品较多,不易定界分类。通过对有关文献与本研究的图形分类进行剖析,其结果实质上是以第一因子载荷为主,第二因子载荷为辅,因此,我们采取以第一因子载荷为主、第二因子载荷为辅、参考第三、四因子载荷的分类方法,将样品按5个等级分类,根据一般的分类等级分为上等、中上等、中等、中下等与下等,比重分别为10%、20%、40%、20%、10%。
, 百拇医药
将Q型第一因子载荷值从大到小排序,前25名被评为上等;26~75名被评为中上等;76~175名被评为中等;176~225名被评为中下等;最后25名被评为下等。各类的平均数、总平均数与标准差见表2。 表2 各类的平均数 等级
指标
x1
x2
x3
x4
x5
x6
x7
, http://www.100md.com
x8
x9
250人
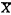
4211.43
170.40
61.48
86.38
7.49
237.57
7.66
239.48
, 百拇医药
14.86
s
659.23
5.86
6.15
4.06
0.43
15.91
3.41
22.39
5.58
上 等
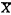
, http://www.100md.com
5310.00
175.36
66.47
88.94
7.44
240.76
6.88
233.34
15.17
中上等
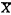
4743.00
, 百拇医药 172.37
62.22
87.35
7.44
241.54
7.42
239.31
15.43
中 等
4205.00
170.43
61.78
, 百拇医药
86.79
7.44
237.91
7.60
237.21
14.94
中下等
3703.00
168.10
60.01
84.95
, 百拇医药 7.64
234.84
7.48
242.94
14.25
下 等
3091.00
165.95
56.70
83.06
7.58
230.56
, 百拇医药
9.56
248.12
14.30
上等(剔70)
5298.00
175.42
66.60
88.85
7.44
240.54
6.75
, 百拇医药 234.20
15.29
中等(剔70)
4277.00
171.09
61.30
86.19
7.49
238.57
7.65
236.48
, 百拇医药 14.92
70号样品
5600.00
173.90
63.30
91.00
7.50
246.00
10.0
212.70
12.20
将Q型第二因子载荷值从大到小排序,找出与上述分类结果不一致的样品。
, 百拇医药
(2)分类不一致的样品的处理 样品70号在第一次分类中分为上等,在第二次分类中分为中等,应该分在哪个等级呢?这里采用求最短距离与用相似系数判断的方法,距离公式为:
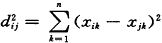
相似系数取两个样品的相关系数。
分别计算除去70号样品的两类的平均数,见表2中的上等(剔70)与中等(剔70)行。为了消除量纲对计算结果的影响,分别将该样品与剔除其上等、中等的指标进行标准化处理。用处理后的值计算该样品与它们的距离、相关系数。与上等类的距离为3.12、相关系数为0.99998;与中等类的距离为7.83、相关系数为0.99983,故将该样品归入上等类。对其他分类不一致的样品进行同样的处理。
同理,可对Q型第三、四因子载荷值从大到小排序,用上述同样的方法判别归类。
, 百拇医药
经过以上重新归类,5个等级的人数有所变化,分别为29、52、94、49、26,所占的比重分别为:11.6%、20.8%、37.6%、19.6%、10.4%。调整归类后的比重有较大变化时,应参考第一因子的分类。
3.R型因子分析
(1)分类 取R型因子分析的前两个因子在平面上绘制散点图,肺活量指标在平面的左侧,与上等类样品在一个类区;其余指标均在右侧,与下等类样品在一个类区。散点较分散,指标之间的分类趋势不明显。
(2)指标的重要性分析 由R型因子分析载荷矩阵的第一因子载荷知,指标肺活量、身高、立定跳远与1 000米的绝对值较大,因此,可以认为是相对重要的指标,事实上,它们是不同类指标的代表。
小 结
1.本文利用对应分析方法,解决了体质调研中大样本样品分类的问题,当根据几个因子载荷值的分类不一致时,可用两点间距离公式或相似系数等方法进行调整。同时也能对指标进行分类、对指标的重要性进行分析以及研究与样品的关系,因此,有一定的实用价值。
, 百拇医药
2.本文的计算量较大,可编制程序进行计算,对计算机内存等方面的要求也不高,具有一定的可行性;本文的研究除了对所研究对象进行分类外,还可利用该结果对所属总体的其他样本进行分类,具有一定的通用性。
参考文献
1.林少宫.多元统计分析及计算程序.武汉:华中工学院出版社,1987.,229~246
2.成都地质学院.《概率论与数理统计》编写小组.《概率论与数理统计》.北京:地质出版社,1981,367~382
3.中国学生体质与健康研究组,95中国学生体质与健康调查研报告.长春:吉林科学技术出版社,1996, http://www.100md.com