配对资料McNemar检验法的适用范围
作者:罗明奎
单位:第三军医大学(400038)
关键词:
中国卫生统计990330 医学研究中,要判断治疗对某症状是否有显著改善,常常将同一病人就治疗前和治疗后进行配对观测。由于治疗前后两种状态下某症状有或无是针对同一病人,因此所得资料称作相依配对计数资料(表1)。
表1 相依配对计数资料
治疗后具有症状A
治疗后不具有症状A
治疗前不具有症状A
a
b
, 百拇医药
治疗前具有症状A
c
d
1.McNemar检验法
针对表1资料,要判断治疗对某症状A是否有疗效,即检验治疗前具有症状A的概率与治疗后具有症状A的概率是否相等,McNemar检验法构造如下:
检验统计量:
当n→∞时且治疗前后症状A发生的概率相等时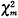 渐近服从自由度为1的χ2分布,其中n=a+b+c+d。
渐近服从自由度为1的χ2分布,其中n=a+b+c+d。
, 百拇医药 检验法则:(1)如果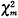 观测值小于χ2α(1),则在显著水平α下认为治疗对症状A无显著疗效;(2)如果
观测值小于χ2α(1),则在显著水平α下认为治疗对症状A无显著疗效;(2)如果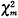 观测值大于等于
观测值大于等于 ,则在显著水平α下认为治疗对症状A有显著疗效。
,则在显著水平α下认为治疗对症状A有显著疗效。
2.McNemar方法与K.Pearson方法的同一性
对一个统计方法的掌握关键在于掌握问题的实质及方法的适用范围,以便对统计方法进行正确应用。
引入随机变量ξ和η如下:
, 百拇医药
检验问题实质是检验如下零假设及备择假设: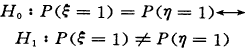
(1)
假定(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布,结合H0对p1,p2,p3,p4中独立参数进行极大似然估计可得(p1,p2,p3,p4)的估计量(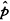 1,
1,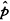 2,
2,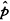 3,
3,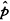 4),按K.Pearson检验法思想,构造统计量为:
4),按K.Pearson检验法思想,构造统计量为:
, 百拇医药
(2)
当(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布且H0成立时,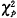 渐近服从自由度为1的χ2分布。容易算得
渐近服从自由度为1的χ2分布。容易算得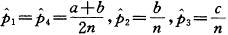 ,代入(2)式得:
,代入(2)式得:
可以看出McNemar方法与K.Pearson方法两者统计量及渐近分布是相同的,因此两者具有一致性。
为了避免McNemar方法的误用,有必要对方法的适用范围加以说明。
, 百拇医药
1.大样本性
由于检验统计量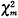 的分布为渐近χ2分布,因此使用时要求样本容量n应尽可能大些,一般要求n大于100。关于这一点在实验中应引起充分重视。
的分布为渐近χ2分布,因此使用时要求样本容量n应尽可能大些,一般要求n大于100。关于这一点在实验中应引起充分重视。
2.各格例数不得小于5
虽然统计量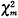 中未涉及b和c,但根据McNemar方法与K.Pearson方法的同一性及K.Pearson检验法的使用经验,仍须要求各格例数均大于5为宜。实验中如没有满足此要求,可在相同实验条件下补充样本以满足要求;如因实验条件所限不能满足此要求,可采用如下修正McNemar检验:
中未涉及b和c,但根据McNemar方法与K.Pearson方法的同一性及K.Pearson检验法的使用经验,仍须要求各格例数均大于5为宜。实验中如没有满足此要求,可在相同实验条件下补充样本以满足要求;如因实验条件所限不能满足此要求,可采用如下修正McNemar检验:
, 百拇医药
3.自然转化概率应相等
由于治疗往往伴随一个时间过程,如果治疗过程中病人由有症状A自然转化为无症状A的概率p10与由无症状A自然转化为有症状A的概率p10不相等,则不宜采用McNemar检验法。事实上,如果p01≠p01,则考察治疗对症状A有无作用,体现为检验如下零假设及备择假设:
(3)
问题(3)的处理较为复杂,这里不作专门讨论。
4.多项分布性
McNemar检验法使用的前提是(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布,因此,收集数据时应随机抽取n例病人进行配对实验以观测各格实际例数分布,以满足多项分布要求,尽量不要人为分组进行实验。
参考文献
1.庄楚强,吴亚森.应用数理统计基础.广州:华南理工大学出版社,1993,245~259.
2.郭祖超.医用数理统计方法.北京:人民卫生出版社,1987,169~176.
3.刘韵源,周家丽.列联表分析.北京:科学出版社,1980,19~21.
4.张尧庭.定性资料的统计分析.桂林:广西师范大学出版社,1991,78~85., 百拇医药
单位:第三军医大学(400038)
关键词:
中国卫生统计990330 医学研究中,要判断治疗对某症状是否有显著改善,常常将同一病人就治疗前和治疗后进行配对观测。由于治疗前后两种状态下某症状有或无是针对同一病人,因此所得资料称作相依配对计数资料(表1)。
表1 相依配对计数资料
治疗后具有症状A
治疗后不具有症状A
治疗前不具有症状A
a
b
, 百拇医药
治疗前具有症状A
c
d
1.McNemar检验法
针对表1资料,要判断治疗对某症状A是否有疗效,即检验治疗前具有症状A的概率与治疗后具有症状A的概率是否相等,McNemar检验法构造如下:
检验统计量:

当n→∞时且治疗前后症状A发生的概率相等时
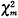 渐近服从自由度为1的χ2分布,其中n=a+b+c+d。
渐近服从自由度为1的χ2分布,其中n=a+b+c+d。, 百拇医药 检验法则:(1)如果
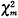 观测值小于χ2α(1),则在显著水平α下认为治疗对症状A无显著疗效;(2)如果
观测值小于χ2α(1),则在显著水平α下认为治疗对症状A无显著疗效;(2)如果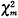 观测值大于等于
观测值大于等于 ,则在显著水平α下认为治疗对症状A有显著疗效。
,则在显著水平α下认为治疗对症状A有显著疗效。2.McNemar方法与K.Pearson方法的同一性
对一个统计方法的掌握关键在于掌握问题的实质及方法的适用范围,以便对统计方法进行正确应用。
引入随机变量ξ和η如下:

, 百拇医药
检验问题实质是检验如下零假设及备择假设:
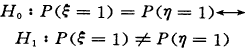
(1)
假定(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布,结合H0对p1,p2,p3,p4中独立参数进行极大似然估计可得(p1,p2,p3,p4)的估计量(
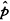 1,
1,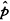 2,
2,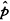 3,
3,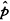 4),按K.Pearson检验法思想,构造统计量为:
4),按K.Pearson检验法思想,构造统计量为:
, 百拇医药
(2)
当(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布且H0成立时,
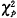 渐近服从自由度为1的χ2分布。容易算得
渐近服从自由度为1的χ2分布。容易算得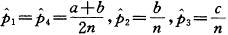 ,代入(2)式得:
,代入(2)式得:
可以看出McNemar方法与K.Pearson方法两者统计量及渐近分布是相同的,因此两者具有一致性。
为了避免McNemar方法的误用,有必要对方法的适用范围加以说明。
, 百拇医药
1.大样本性
由于检验统计量
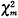 的分布为渐近χ2分布,因此使用时要求样本容量n应尽可能大些,一般要求n大于100。关于这一点在实验中应引起充分重视。
的分布为渐近χ2分布,因此使用时要求样本容量n应尽可能大些,一般要求n大于100。关于这一点在实验中应引起充分重视。2.各格例数不得小于5
虽然统计量
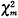 中未涉及b和c,但根据McNemar方法与K.Pearson方法的同一性及K.Pearson检验法的使用经验,仍须要求各格例数均大于5为宜。实验中如没有满足此要求,可在相同实验条件下补充样本以满足要求;如因实验条件所限不能满足此要求,可采用如下修正McNemar检验:
中未涉及b和c,但根据McNemar方法与K.Pearson方法的同一性及K.Pearson检验法的使用经验,仍须要求各格例数均大于5为宜。实验中如没有满足此要求,可在相同实验条件下补充样本以满足要求;如因实验条件所限不能满足此要求,可采用如下修正McNemar检验:
, 百拇医药
3.自然转化概率应相等
由于治疗往往伴随一个时间过程,如果治疗过程中病人由有症状A自然转化为无症状A的概率p10与由无症状A自然转化为有症状A的概率p10不相等,则不宜采用McNemar检验法。事实上,如果p01≠p01,则考察治疗对症状A有无作用,体现为检验如下零假设及备择假设:

(3)
问题(3)的处理较为复杂,这里不作专门讨论。
4.多项分布性
McNemar检验法使用的前提是(a,b,c,d)服从参数为(p1,p2,p3,p4)的多项分布,因此,收集数据时应随机抽取n例病人进行配对实验以观测各格实际例数分布,以满足多项分布要求,尽量不要人为分组进行实验。
参考文献
1.庄楚强,吴亚森.应用数理统计基础.广州:华南理工大学出版社,1993,245~259.
2.郭祖超.医用数理统计方法.北京:人民卫生出版社,1987,169~176.
3.刘韵源,周家丽.列联表分析.北京:科学出版社,1980,19~21.
4.张尧庭.定性资料的统计分析.桂林:广西师范大学出版社,1991,78~85., 百拇医药