无金标准情况下诊断试验的评价方法
作者：顾海雁 陈启光
单位：顾海雁 南通医学院医学统计学教研室(226001); 陈启光 南京铁道医学院卫生统计学教研室(210009)
关键词：诊断试验；无金标准；Bayesian参数估计；Gibbs抽样
中国卫生统计990404 【提 要】 目的 探讨无金标准情况下诊断试验的评价方法及患病率的估计。方法 从Beyesian参数估计原理出发，用Gibbs抽样法完成参数后验密度的估计。结果 将有金标准的资料作为无金标准处理，所得参数估计值前后吻合，效果良好，并可得到参数的后验密度分布图。结论 上述方法可有效地估计无金标准情况下诊断试验的评价参数。
Diagnostic Test Assessment in the Absence of Gold Standard
, http://www.100md.com
Gu Haiyan,Dept.of Health Statistics,Nantong medical college(226001),Chen Qiguang,Dept.of Health statistics,Nanjing railway medical college(210009),Nanjing
【Abstract】 Objective To find out an estimating method for prevalence and the parameters of diagnostic tests in the absence of gold standard.Methods Bayesian estimation theory is used.Marginal posterior densities of all parameters are estimated using Gibbs sampler.Results We illustrate the methods using data sets that are in the presence of gold standard.The results of diagnostic test assessment are homogeneously either presence or absence of gold standard.We can also obtain the distribution of these parameters.Conclusion The method can be used to assess diagnostic test and estimate prevalence effectively in the absence of gold standard.
, 百拇医药
【Key words】 Diagnostic test Absence of gold standard Bayesian estimation Gibbs sampler
诊断试验评价方法的研究和应用一般都建立在与“金标准”比较的基础上。但是，实际工作中“金标准”往往难以获得，因而，无金标准情况下诊断试验的评价具有实际意义。本文借助Bayesian参数估计原理，采用无需严格考虑资料分布的统计模拟抽样技术，解决了无金标准情况下诊断试验的评价及患病率的估计问题。
方 法
通常用表1表示两个诊断试验的结果：四个实际观察值分别用符号表示为u、v、w、x，其相应的潜在真值记为Y1、Y2、Y3、Y4。评价诊断试验常把灵敏度Se、特异度Sp作为评价指标，分别简记作S和C。两个诊断试验有5个待估参数：患病率π、S1、C1、S2、C2，由于Se和Sp相互影响并不独立，又随着π的变化而变化，这些参数可根据Bayes原理按照条件概率计算而得。Bayesian参数估计方法的基本思想为：参数后验密度与先验密度和似然函数之积成比例〔2～4〕，即：h(θ｜x1,…，xn)∝π(θ)l(θ/x1,…，xn)。后验密度h(θ｜x1,x2，…，xn)既包含了先验分布π(θ)信息，又揉和了样本对参数的条件分布l(θ｜x1,x2，…，xn)，是样本信息和过去经验的结合。
, 百拇医药
表1 两诊断试验的观察结果 试验1
试验2
合计
+
-
+
-
27(u)/(Y1)
5(w)/(Y3)
59(v)/(Y2)
59(x)/(Y4)
, 百拇医药
86(u+v)
64(w+x)
合计
32(u+w)
118(v+x)
150(N)
1.先验分布的选取
根据共轭分布原理〔1〕，选用Beta(α、β)分布作为先验分布，其概率密度形式如下〔2，3〕：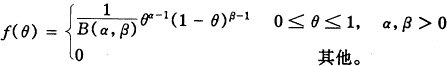
(1)
π、Se、Sp的先验分布都服从Beta分布，分别记Beta(απ，βπ)，Beta(αs，βs)和Beta(αc，βc)。为了方便α、β的估计，可将Beta(α，β)换用Beta(μ，M)表达〔3〕，其中μ=α/(α+β)，表示先验的平均值；M=α+β，表示先验的精度，两者的关系是：
, http://www.100md.com
V(θ｜μ,M)=μ(1-μ)/(M+1)
(2)
试验1的阳性数为(u+v)，简记为a，其边缘分布是Beta-Binomial分布〔2〕，密度形式可记作：
(3)
试验2的阳性数(u+w)的边缘分布及其密度形式亦可用上法计算。以既往资料和专业知识为依据，给出π、Se、Sp所在可能区间范围。区间中点为平均值μ，区间的1/4距离的平方作为方差，用式(2)、(3)可估计出先验分布的参数；患病率一般未知，根据概率统计理论，只有均匀分布时熵才达到最大值〔1，4〕，因此，取患病率的先验分布为均匀分布，其参数为(1，1)。
, 百拇医药 2.似然函数
表1资料的似然函数由附录所述可推导出如下算式：
l(u,v,w,x,Y1，Y2，Y3，Y4｜π，S1，C1，S2，C2)
=〔πS1S2〕Y1〔(1-π)(1-C1)(1-C2)〕u-Y1〔πS1(1-S2)〕
Y2〔(1-π)(1-C1)C2〕v-Y2〔πS2(1-S1)〕Y3〔(1-π)C1(1-C2)〕
, http://www.100md.com
w-Y3〔π(1-S1)(1-S2)〕Y4〔(1-π)C1C2〕x-Y4
(4)
3.计算方法
利用(Markov Chain Monte Carlo)MCMC技术，选用适合于全条件分布的Gibbs抽样算法构建Markov链〔5〕，完成Bayesian估计中高维积分的近似计算。Gibbs抽样算法程序的实现可以用英国S-Plus软件或BUGS软件〔6，7〕实现。
实例分析
本文将有金标准资料当作无金标准考核上述方法的可行性。资料来源于南京医科大学国家八五攻关课题“日本血吸虫单克隆抗体特型抗体NP30应用性研究”，正常对照血清50例来自非血吸虫流行区，慢性日本血吸虫病人血清100例均证实为感染者，用两种方法采用双盲方法分别检测，如表1数据。灵敏度、特异度的先验信息列在表2。Gibbs抽样迭代次数共为20 500次，经尝试，本研究的资料经500次迭代已满足收敛要求。为此用后20 000次迭代结果作为Markov链进行参数估计。结果与真值相近，效果良好，同时可计算得到诊断试验的阳性预测(PPV)值和阴性预测值(NPV)，见表3。S和C及患病率的分布图可借助Gibbs抽样结果完成，见图1和图2。
, 百拇医药
表2 诊断试验先验信息及其先验分布参数
试验1
试验2
范围
α
β
范围
α
β
Se
0.50～0.85
17.61
8.48
, http://www.100md.com
0.10～0.50
6.00
14.00
Sp
0.80～1.00
28.90
2.86
0.80～1.00
28.90
2.86
表3 无金标准情况下诊断试验评价参数的估计
真值
, 百拇医药
Gibbs抽样法计算结果
M
95%CI
π
0.67
0.68
0.53～0.84
S1
0.81
0.77
0.64～0.88
试验1
, http://www.100md.com C1
PPV1
0.90
0.94
0.91
0.94
0.78～0.98
0.81～0.99
NPV1
0.70
0.71
0.48～0.86
, 百拇医药
S2
0.29
0.30
0.21～0.40
试验2
C2
PPV2
0.94
0.90
0.95
0.90
0.87～0.99
, 百拇医药
0.75～0.98
NPV2
0.40
0.46
0.31～0.60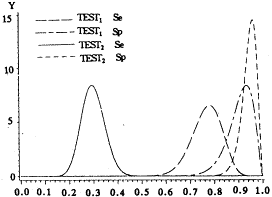
图1 诊断试验灵敏度、特异度的后验密度分布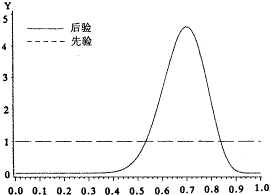
图2 Gibbs抽样法估计患病率分布
讨 论
诊断试验评价是临床流行病学中常见的问题之一，从统计学角度来说，是通过计算来研究事物的条件概率或找出该事物在某测定项目的特异值实现的，很多情况下依赖与“金标准”进行盲法和同步比较得到结论。实际情况中并不存在“完美”的试验，不可能使灵敏度和特异度均达到100%。“金标准”是随时间和实践知识的积累而不断完善的，在一定时期内相对稳定的标准，在实际操作上往往费用高和(或)创伤性较大，一般也难以得到。因此，如何在缺乏金标准的情况下评价诊断实验尤为有意义。
, 百拇医药
患病率的估计通常要借助诊断试验，估计值难免过低或过高；而不同的患病率对诊断试验的预测值又有影响。因此，诊断试验的评价建立在一定患病率的基础上，在没有金标准的基础上，我们从Bayesian参数估计原理出发，以参数呈全条件分布为基础，用Gibbs抽样法计算参数的条件后验密度，能够较好地估计患病率的值，表1资料中参数的估计原理见附录。
Bayesian原理估计参数不可避免要应用先验分布。先验分布一般依靠历史资料、专家经验和预试验结果等提供信息，也可依照实际情况设定。当患病率未知，诊断试验又没有先验信息时，建议在小范围内进行“预试验”以获取先验信息。经过尝试我们发现，先验信息是不可被一些数学技术手段弥补的，各参数均无先验所得的结果，不如有先验信息所得结果理想。
MCMC技术中的Monte Carlo积分是从需要的分布中抽取样本，产生样本均数和近似期望值。Markov链就是一个很巧妙的样本，产生这个来自于指定平稳分布的样本是MCMC的难点之一。构造Markov链的方法有很多，大都以Metropolis和Hastings(1953)等的工作为模式〔6〕，Gibbs抽样就是其中的一种，具体请参考有关文献。本文为了说明方法的可行性，权且将有金标准资料当作无金标准进行尝试，并将结果与真值进行比较，吻合度较好，各参数的分布图形均可由此得到。
, 百拇医药
本文列举了无金标准情况下两个诊断试验的评价方法，从理论上讲多个试验提供的信息将更多。但随着试验个数n的增加，待估参数个数也呈几何级数增长，参数后验密度的计算涉及更多的条件，其技术难度将大大提高，这方面值得进一步探讨。
(本文资料由南京医科大学管晓虹教授提供，论文的完成得到了加拿大McGill大学Lawrence Joseph博士和南通医学院陈峰博士的帮助，特此表示感谢。)
参考文献
1.张尧庭，陈汉峰.贝叶斯统计推断.北京：科学出版社，1991，27～31，36～40.
2.Carlin BP and Louis TA.Bayes and empirical Bayes mehods for data analysis.London:Chapman & Hall,1996，21～38.
, 百拇医药
3.Tarone RE.The use of historical control information in testing for a trend in proportions.Biometics.1982,38:215～220
4.Joseph L,Gyorkos TW and Coupal L.Bayesian estimation of disease prevalence and the Parameters of diagnostic tests in the absence of a gold standard.American Journal of Epidemiology.1995,141(3):263～272.
5.Gilk WR,Richardson S and Spiegelhalter DJ.Markov Chain Monte Carlo in.Practice.London:Chapman & Hall 1996，12.
, 百拇医药
6.Spector Phil.An Introduction to S and S-Plus.Duxbury Press,1994，43～73.
7.Spiegelhalter D,Thomas A,Nicky B et al.BUGS0.5 Bayesian Inference Using Gibbs Sampling Manual(version ii).MRC Biostatistics Unit,Institute of Public Health,Cambridge CB2 2SR.1996.5，14～25.
附 录
Gibbs抽样法适用于全条件分布(full conditional distribution):用π(x)=π(x1，x2，…，xk)表示π(x)的联合密度，若其中每个xi的计算都建立在其余x的基础上，则π(x)称为全条件分布。实际应用中并不是每个参数的计算都必须依赖于所有其他参数。表1资料中各评价参数的后验密度算法表达式如下：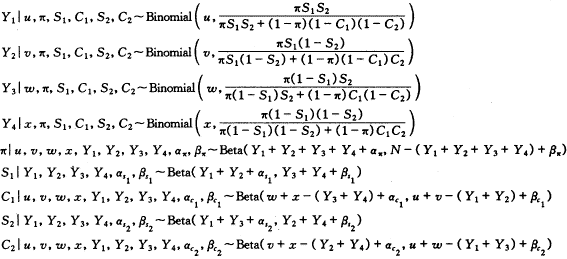
, 百拇医药
单位：顾海雁 南通医学院医学统计学教研室(226001); 陈启光 南京铁道医学院卫生统计学教研室(210009)
关键词：诊断试验；无金标准；Bayesian参数估计；Gibbs抽样
中国卫生统计990404 【提 要】 目的 探讨无金标准情况下诊断试验的评价方法及患病率的估计。方法 从Beyesian参数估计原理出发，用Gibbs抽样法完成参数后验密度的估计。结果 将有金标准的资料作为无金标准处理，所得参数估计值前后吻合，效果良好，并可得到参数的后验密度分布图。结论 上述方法可有效地估计无金标准情况下诊断试验的评价参数。
Diagnostic Test Assessment in the Absence of Gold Standard
, http://www.100md.com
Gu Haiyan,Dept.of Health Statistics,Nantong medical college(226001),Chen Qiguang,Dept.of Health statistics,Nanjing railway medical college(210009),Nanjing
【Abstract】 Objective To find out an estimating method for prevalence and the parameters of diagnostic tests in the absence of gold standard.Methods Bayesian estimation theory is used.Marginal posterior densities of all parameters are estimated using Gibbs sampler.Results We illustrate the methods using data sets that are in the presence of gold standard.The results of diagnostic test assessment are homogeneously either presence or absence of gold standard.We can also obtain the distribution of these parameters.Conclusion The method can be used to assess diagnostic test and estimate prevalence effectively in the absence of gold standard.
, 百拇医药
【Key words】 Diagnostic test Absence of gold standard Bayesian estimation Gibbs sampler
诊断试验评价方法的研究和应用一般都建立在与“金标准”比较的基础上。但是，实际工作中“金标准”往往难以获得，因而，无金标准情况下诊断试验的评价具有实际意义。本文借助Bayesian参数估计原理，采用无需严格考虑资料分布的统计模拟抽样技术，解决了无金标准情况下诊断试验的评价及患病率的估计问题。
方 法
通常用表1表示两个诊断试验的结果：四个实际观察值分别用符号表示为u、v、w、x，其相应的潜在真值记为Y1、Y2、Y3、Y4。评价诊断试验常把灵敏度Se、特异度Sp作为评价指标，分别简记作S和C。两个诊断试验有5个待估参数：患病率π、S1、C1、S2、C2，由于Se和Sp相互影响并不独立，又随着π的变化而变化，这些参数可根据Bayes原理按照条件概率计算而得。Bayesian参数估计方法的基本思想为：参数后验密度与先验密度和似然函数之积成比例〔2～4〕，即：h(θ｜x1,…，xn)∝π(θ)l(θ/x1,…，xn)。后验密度h(θ｜x1,x2，…，xn)既包含了先验分布π(θ)信息，又揉和了样本对参数的条件分布l(θ｜x1,x2，…，xn)，是样本信息和过去经验的结合。
, 百拇医药
表1 两诊断试验的观察结果 试验1
试验2
合计
+
-
+
-
27(u)/(Y1)
5(w)/(Y3)
59(v)/(Y2)
59(x)/(Y4)
, 百拇医药
86(u+v)
64(w+x)
合计
32(u+w)
118(v+x)
150(N)
1.先验分布的选取
根据共轭分布原理〔1〕，选用Beta(α、β)分布作为先验分布，其概率密度形式如下〔2，3〕：
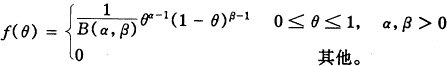
(1)
π、Se、Sp的先验分布都服从Beta分布，分别记Beta(απ，βπ)，Beta(αs，βs)和Beta(αc，βc)。为了方便α、β的估计，可将Beta(α，β)换用Beta(μ，M)表达〔3〕，其中μ=α/(α+β)，表示先验的平均值；M=α+β，表示先验的精度，两者的关系是：
, http://www.100md.com
V(θ｜μ,M)=μ(1-μ)/(M+1)
(2)
试验1的阳性数为(u+v)，简记为a，其边缘分布是Beta-Binomial分布〔2〕，密度形式可记作：
(3)
试验2的阳性数(u+w)的边缘分布及其密度形式亦可用上法计算。以既往资料和专业知识为依据，给出π、Se、Sp所在可能区间范围。区间中点为平均值μ，区间的1/4距离的平方作为方差，用式(2)、(3)可估计出先验分布的参数；患病率一般未知，根据概率统计理论，只有均匀分布时熵才达到最大值〔1，4〕，因此，取患病率的先验分布为均匀分布，其参数为(1，1)。
, 百拇医药 2.似然函数
表1资料的似然函数由附录所述可推导出如下算式：
l(u,v,w,x,Y1，Y2，Y3，Y4｜π，S1，C1，S2，C2)
=〔πS1S2〕Y1〔(1-π)(1-C1)(1-C2)〕u-Y1〔πS1(1-S2)〕
Y2〔(1-π)(1-C1)C2〕v-Y2〔πS2(1-S1)〕Y3〔(1-π)C1(1-C2)〕
, http://www.100md.com
w-Y3〔π(1-S1)(1-S2)〕Y4〔(1-π)C1C2〕x-Y4
(4)
3.计算方法
利用(Markov Chain Monte Carlo)MCMC技术，选用适合于全条件分布的Gibbs抽样算法构建Markov链〔5〕，完成Bayesian估计中高维积分的近似计算。Gibbs抽样算法程序的实现可以用英国S-Plus软件或BUGS软件〔6，7〕实现。
实例分析
本文将有金标准资料当作无金标准考核上述方法的可行性。资料来源于南京医科大学国家八五攻关课题“日本血吸虫单克隆抗体特型抗体NP30应用性研究”，正常对照血清50例来自非血吸虫流行区，慢性日本血吸虫病人血清100例均证实为感染者，用两种方法采用双盲方法分别检测，如表1数据。灵敏度、特异度的先验信息列在表2。Gibbs抽样迭代次数共为20 500次，经尝试，本研究的资料经500次迭代已满足收敛要求。为此用后20 000次迭代结果作为Markov链进行参数估计。结果与真值相近，效果良好，同时可计算得到诊断试验的阳性预测(PPV)值和阴性预测值(NPV)，见表3。S和C及患病率的分布图可借助Gibbs抽样结果完成，见图1和图2。
, 百拇医药
表2 诊断试验先验信息及其先验分布参数
试验1
试验2
范围
α
β
范围
α
β
Se
0.50～0.85
17.61
8.48
, http://www.100md.com
0.10～0.50
6.00
14.00
Sp
0.80～1.00
28.90
2.86
0.80～1.00
28.90
2.86
表3 无金标准情况下诊断试验评价参数的估计
真值
, 百拇医药
Gibbs抽样法计算结果
M
95%CI
π
0.67
0.68
0.53～0.84
S1
0.81
0.77
0.64～0.88
试验1
, http://www.100md.com C1
PPV1
0.90
0.94
0.91
0.94
0.78～0.98
0.81～0.99
NPV1
0.70
0.71
0.48～0.86
, 百拇医药
S2
0.29
0.30
0.21～0.40
试验2
C2
PPV2
0.94
0.90
0.95
0.90
0.87～0.99
, 百拇医药
0.75～0.98
NPV2
0.40
0.46
0.31～0.60
图1 诊断试验灵敏度、特异度的后验密度分布
图2 Gibbs抽样法估计患病率分布
讨 论
诊断试验评价是临床流行病学中常见的问题之一，从统计学角度来说，是通过计算来研究事物的条件概率或找出该事物在某测定项目的特异值实现的，很多情况下依赖与“金标准”进行盲法和同步比较得到结论。实际情况中并不存在“完美”的试验，不可能使灵敏度和特异度均达到100%。“金标准”是随时间和实践知识的积累而不断完善的，在一定时期内相对稳定的标准，在实际操作上往往费用高和(或)创伤性较大，一般也难以得到。因此，如何在缺乏金标准的情况下评价诊断实验尤为有意义。
, 百拇医药
患病率的估计通常要借助诊断试验，估计值难免过低或过高；而不同的患病率对诊断试验的预测值又有影响。因此，诊断试验的评价建立在一定患病率的基础上，在没有金标准的基础上，我们从Bayesian参数估计原理出发，以参数呈全条件分布为基础，用Gibbs抽样法计算参数的条件后验密度，能够较好地估计患病率的值，表1资料中参数的估计原理见附录。
Bayesian原理估计参数不可避免要应用先验分布。先验分布一般依靠历史资料、专家经验和预试验结果等提供信息，也可依照实际情况设定。当患病率未知，诊断试验又没有先验信息时，建议在小范围内进行“预试验”以获取先验信息。经过尝试我们发现，先验信息是不可被一些数学技术手段弥补的，各参数均无先验所得的结果，不如有先验信息所得结果理想。
MCMC技术中的Monte Carlo积分是从需要的分布中抽取样本，产生样本均数和近似期望值。Markov链就是一个很巧妙的样本，产生这个来自于指定平稳分布的样本是MCMC的难点之一。构造Markov链的方法有很多，大都以Metropolis和Hastings(1953)等的工作为模式〔6〕，Gibbs抽样就是其中的一种，具体请参考有关文献。本文为了说明方法的可行性，权且将有金标准资料当作无金标准进行尝试，并将结果与真值进行比较，吻合度较好，各参数的分布图形均可由此得到。
, 百拇医药
本文列举了无金标准情况下两个诊断试验的评价方法，从理论上讲多个试验提供的信息将更多。但随着试验个数n的增加，待估参数个数也呈几何级数增长，参数后验密度的计算涉及更多的条件，其技术难度将大大提高，这方面值得进一步探讨。
(本文资料由南京医科大学管晓虹教授提供，论文的完成得到了加拿大McGill大学Lawrence Joseph博士和南通医学院陈峰博士的帮助，特此表示感谢。)
参考文献
1.张尧庭，陈汉峰.贝叶斯统计推断.北京：科学出版社，1991，27～31，36～40.
2.Carlin BP and Louis TA.Bayes and empirical Bayes mehods for data analysis.London:Chapman & Hall,1996，21～38.
, 百拇医药
3.Tarone RE.The use of historical control information in testing for a trend in proportions.Biometics.1982,38:215～220
4.Joseph L,Gyorkos TW and Coupal L.Bayesian estimation of disease prevalence and the Parameters of diagnostic tests in the absence of a gold standard.American Journal of Epidemiology.1995,141(3):263～272.
5.Gilk WR,Richardson S and Spiegelhalter DJ.Markov Chain Monte Carlo in.Practice.London:Chapman & Hall 1996，12.
, 百拇医药
6.Spector Phil.An Introduction to S and S-Plus.Duxbury Press,1994，43～73.
7.Spiegelhalter D,Thomas A,Nicky B et al.BUGS0.5 Bayesian Inference Using Gibbs Sampling Manual(version ii).MRC Biostatistics Unit,Institute of Public Health,Cambridge CB2 2SR.1996.5，14～25.
附 录
Gibbs抽样法适用于全条件分布(full conditional distribution):用π(x)=π(x1，x2，…，xk)表示π(x)的联合密度，若其中每个xi的计算都建立在其余x的基础上，则π(x)称为全条件分布。实际应用中并不是每个参数的计算都必须依赖于所有其他参数。表1资料中各评价参数的后验密度算法表达式如下：
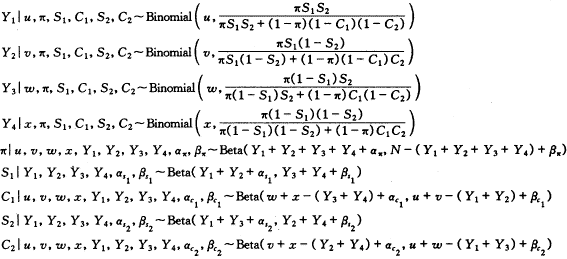, 百拇医药