重复观测数据的半参数回归分析*
作者：王文昌 易东 张蔚 许汝福
单位：王文昌 易东 张蔚 许汝福第三军医大学卫生统计学教研室(400038); 李辉智 西南政法大学刑侦系(400031)
关键词：重复测量数据；半参数回归；参数估计；假设检验
中国卫生统计990403 【提 要】 目的 研究重复观测数据的回归分析技术。方法 利用半参数回归分析的原理与方法，结合重复观测数据的特点，建立重复观测数据的半参数回归模型，并进一步讨论模型参数的估计方法及假设检验公式。结果 讨论了重复观测数据的半参数回归模型的模型误差，分析了重复因素的效应及参数的影响，给出了其模型的方差分析表。结论 通过实例分析，表明对重复观测数据的处理，半参数回归分析的效果优于普通的最小二乘法和广义最小二乘法。
Semiparametric Regression Analysis of Repeated Measurements
, http://www.100md.com
Wang wenchang,Yi Dong.,Zhang wei et al.,Department of Health Statistics,Third Military Medical University,(400038)Chongqing.
【Abstract】 Objective To set up the semiparametric regression models on repeated measurements.Methods Using the theories and methods of semiparametric regression to establish the regression model of repeated measurements and discuss its method of parametric estimation and hypothesis testing.Results The table of the analysis of variance about this model has been got,this table can be used to analyze the effect of the repeated factors and the parameters.Conclusion By analyzing one example,the result shows that semiparametric regression model is better than the ordinary least squares and the generalized least square analysis.
, 百拇医药
【Key words】 Repeated measurements Semiparametric regression Parametric estimation Hypothesis testing
重复测量数据是医学领域中常见的一种数据形式。由于对同一对象进行重复测量，因此其数据间存在自相关性，当对其进行回归分析时，通常的最小二乘法将失效〔1〕。
半参数回归分析是近年来才兴起的一门统计分析技术，其一般模型〔3〕为：
Y=β′X+g(T)+ε
(1)
其中(X，T)∈Rp×R1为独立同分布的随机向量或设计点列，T的支撑集为有界闭集，β为 P×1的未知参数向量，g(.)是定义于一有界闭集上的未知函数，ε为相互独立的随机误差向量，E(ε)=0，E(ε2)=σ2(未知)，且ε与(X，T)相互独立。事实上，模型(1)将Y的影响因素分为两个部分：一部分为线性部分，其因素为处理因素；另一部分为非线性部分，其因素可以为非处理因素。由于模型(1)剔除了非处理因素的影响而单纯考虑处理因素的效应，因而，模型(1)较一般的参数模型有较强的适应性，而又比非参数模型易于解释处理。比如，对重复观测数据，我们可以把“重复”的效应归结于未知函数g中，从而消除“重复”因素带来的数据间的自相关性而单纯考虑处理因素的影响。
, http://www.100md.com
现对模型(1)的研究主要集中在其大样本性质上〔3，4〕，对其小样本性质则研究得较少。我们曾在文献〔5〕中在适当的假设下采用Monte Carlo模拟得到了模型(1)的小样本性质。本文将利用文献〔5〕的一些结果来研究重复观测值的回归问题。
原理与方法
设在研究总体中随机地选出n个受试对象，分别对每一对象重复测量p次，得观测值(Xij，Yij)，i=1,2,…,n, j=1,2,…,p。现分析X与Y间的关系。
对上述重复观测数据，可建立如下半参数回归模型：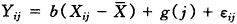
(2)
其中b为模型参数，主要反应了X对Y的影响。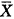
=
为X的平均数。g(j)为未知函数，主要反应了重复测量的效应。εij为随机误差，E(εij)=0，E(
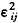)=σ2,且εij相互独立。
, 百拇医药
沿用文献〔5〕中的方法，对模型(2)的参数进行估计。
1.把b看为已知时，g(j)的最小二乘估计为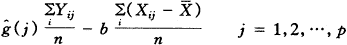
(3)
显然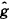
(j)也为g(j)的一个邻近估计。
2.把(3)式代入(2)后b的最小二乘估计为使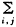
(Yij-bXij-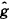(j))2最小的解。为了简便起见，作变换
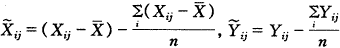，则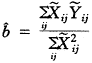
, http://www.100md.com
(4)
事实上，(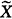
ij，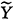
ij)为原始数据消除了自相关性后所得的序列。当假定εij服从N(0，σ2)时，由文献〔5〕结果，σ2的估计式为：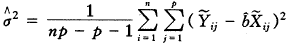
(5)
并且，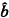
的假设检验可用如下t统计量：
, http://www.100md.com
(6)
总变异的分解
记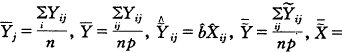
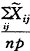。并注意到
，有：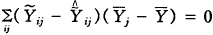
(7)
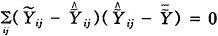
(8)
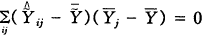
(9)
, 百拇医药
上面3个式子表明，
是相互独立的。而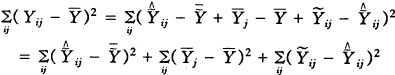
(10)
事实上，对b进行最小二乘估计时，是拟合如下线性模型：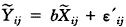
(11)
显然，ε′ij=εij+g(j)-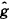(j)，由于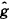(j)收敛与g(j)，因此，当N较大时，可假定ε′ij与εij同分布，即ε′ij也服从N(0，σ2)且相互独立。于是，在(10)式中，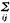
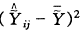可解释为模型(2)中参数的回归平方和；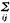
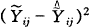可解释为模型(2)的误差平方和；显然，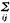
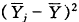为重复观测所引起的变异。注意到(6)式中模型误差的自由度为np-p-1。于是对模型(1)的假设检验可用如下方差分析表：
, 百拇医药
表1 模型(1)的方差分析表 变异来源
SS
v
MS
F
总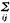(Yij-
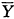)2
np
回归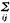
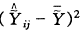
, 百拇医药
1
SSreg/vreg
MSreg/MSerr
重复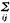
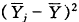
p
SSrep/vrep
MSrep/MSerr
误差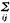
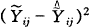
, 百拇医药
np-p-1
SSerr/verr
显然，在方差分析表中对回归系数的假设检验与(4)式中的t检验公式等价。并且根据方差分析中一般的自由度分解原理，文献〔5〕对误差的自由的模拟结果是可靠的。实 例
表2为某幼儿园9名幼儿连续3年的体重与身高数据。文献〔2〕曾分析得受试对象内残差相关是显著的。并且对体重与身高数据使用普通最小二乘法得到的回归系数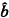的标准误将高估真实的标准误。于是在文献〔5〕中对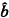的标准误进行调整后，得到对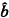的假设检验的t值为：6.2667，同时采用广义最小二乘法也得到t=9.9808，进一步说明了对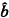的假设检验是显著的，即幼儿身高与体重有显著关系的结论。事实上，我们分别对1991年、1992年、1993年数据建立线性回归方程，则3个t值分别为：1.4744、0.6474、1.1136。也就是说，对此资料而言，如果剔除年龄因素的影响，幼儿的身高与体重应该是无关的。我们现用模型(2)来讨论表2中的数据，则有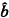：=0.2514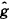，(1)=18.6116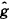，(2)=19.4563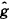，(3)=19.5611。对其半参数回归模型进行假设检验得到方差分析表(表3)。
, http://www.100md.com
表2 某幼儿园幼儿的体重与身高 编号
观测日期
1991年
(6/7)
1992年
(25/5)
1993年
(24/5)
1
X(cm)
105.0
113.7
, 百拇医药 120.0
Y(kg)
16.3
18.7
19.7
2
X(cm)
102.5
110.3
117.0
Y(kg)
16.2
20.3
, 百拇医药
23.5
3
X(cm)
104.5
110.4
117.7
Y(kg)
15.81
18.4
20.4
4
X(cm)
109.8
, 百拇医药
117.1
124.4
Y(kg)
16.1
18.6
21.0
5
X(cm)
103.8
110.0
112.0
Y(kg)
17.0
, 百拇医药
19.0
18.55
6
X(cm)
106.0
113.7
120.7
Y(kg)
16.1
17.8
19.3
7
X(cm)
, 百拇医药
110.3
115.8
123.7
Y(kg)
20.3
24.3
27.9
8
X(cm)
103.0
110.5
116.2
Y(kg)
, 百拇医药
17.3
19.7
21.6
9
X(cm)
106.9
113.1
121.0
Y(kg)
17.0
18.7
19.1
表3 对表2数据拟合模型(2)的方差分析表 变异来源
, 百拇医药
SS
v
MS
F
P
总
198.90
27
回归
15.05
1
15.05
3.51
, 百拇医药 >0.05
重复
85.31
3
28.44
6.64
<0.01
误差
98.54
23
4.28
由表3可看出，对幼儿而言，如果剔除年龄因素的影响时，身高与体重是无关的，而对体重影响的主要因素为年龄因素。当仅使用公式(6)对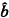进行假设检验得：t=1.8735，即为表3中回归因素的F值的平方根，与分别对3年的数据讨论得到的t值较为接近。讨 论
, 百拇医药
1.分析幼儿身高与体重的关系应考虑年龄因素的影响。事实上就此资料而言，如果排除年龄因素的影响后，由于幼儿的体重变异远远大于身高的变异而掩盖了身高对体重的影响，幼儿的身高与体重是无关的。
2.对重复测量数据进行回归分析时，由于数据间的自相关性，一般的最小二乘法将失效。事实上，在文献〔2〕中无论是采用对标准误进行调整还是采用广义最小二乘法均得到了与实际资料所显示的信息不相符的结果。此实例的结果显示，半参数回归分析用于处理重复测量数据时的效果优于普通的最小二乘法和广义最小二乘法。
3.由方差分析表可看出，在文献〔5〕中对半参数回归模型的误差的小样本模拟结果是可靠的，并且我们应用半参数回归模型研究重复观测数据的回归问题取得了较好的结果，我们将进一步对在理论上对半参数回归的小样本性质进行研究，拓展半参数回归在医学数据处理中的应用领域。
*国家自然科学基金资助项目(39870691)
, http://www.100md.com
参考文献
1.陈希儒，王松桂.近代回归分析——原理方法及应用.第1版.合肥：安徽教育出版社，1987，91.
2.赵景波，李康.重复观测值线性回归分析及其在医学中的应用.中国卫生统计，1995，12(2)：18.
3.高集体，等.半参数回归模型研究的若干进展.应用概率统计，1994，10(1)：96.
4.洪圣岩.一类半参数模型的估计理论.中国科学(A辑)，1991，12(12)：1258.
5.王文昌，等.季节性时间序列资料预测的半参数回归模型.中国卫生统计，1997，14(6)：4., 百拇医药
单位：王文昌 易东 张蔚 许汝福第三军医大学卫生统计学教研室(400038); 李辉智 西南政法大学刑侦系(400031)
关键词：重复测量数据；半参数回归；参数估计；假设检验
中国卫生统计990403 【提 要】 目的 研究重复观测数据的回归分析技术。方法 利用半参数回归分析的原理与方法，结合重复观测数据的特点，建立重复观测数据的半参数回归模型，并进一步讨论模型参数的估计方法及假设检验公式。结果 讨论了重复观测数据的半参数回归模型的模型误差，分析了重复因素的效应及参数的影响，给出了其模型的方差分析表。结论 通过实例分析，表明对重复观测数据的处理，半参数回归分析的效果优于普通的最小二乘法和广义最小二乘法。
Semiparametric Regression Analysis of Repeated Measurements
, http://www.100md.com
Wang wenchang,Yi Dong.,Zhang wei et al.,Department of Health Statistics,Third Military Medical University,(400038)Chongqing.
【Abstract】 Objective To set up the semiparametric regression models on repeated measurements.Methods Using the theories and methods of semiparametric regression to establish the regression model of repeated measurements and discuss its method of parametric estimation and hypothesis testing.Results The table of the analysis of variance about this model has been got,this table can be used to analyze the effect of the repeated factors and the parameters.Conclusion By analyzing one example,the result shows that semiparametric regression model is better than the ordinary least squares and the generalized least square analysis.
, 百拇医药
【Key words】 Repeated measurements Semiparametric regression Parametric estimation Hypothesis testing
重复测量数据是医学领域中常见的一种数据形式。由于对同一对象进行重复测量，因此其数据间存在自相关性，当对其进行回归分析时，通常的最小二乘法将失效〔1〕。
半参数回归分析是近年来才兴起的一门统计分析技术，其一般模型〔3〕为：
Y=β′X+g(T)+ε
(1)
其中(X，T)∈Rp×R1为独立同分布的随机向量或设计点列，T的支撑集为有界闭集，β为 P×1的未知参数向量，g(.)是定义于一有界闭集上的未知函数，ε为相互独立的随机误差向量，E(ε)=0，E(ε2)=σ2(未知)，且ε与(X，T)相互独立。事实上，模型(1)将Y的影响因素分为两个部分：一部分为线性部分，其因素为处理因素；另一部分为非线性部分，其因素可以为非处理因素。由于模型(1)剔除了非处理因素的影响而单纯考虑处理因素的效应，因而，模型(1)较一般的参数模型有较强的适应性，而又比非参数模型易于解释处理。比如，对重复观测数据，我们可以把“重复”的效应归结于未知函数g中，从而消除“重复”因素带来的数据间的自相关性而单纯考虑处理因素的影响。
, http://www.100md.com
现对模型(1)的研究主要集中在其大样本性质上〔3，4〕，对其小样本性质则研究得较少。我们曾在文献〔5〕中在适当的假设下采用Monte Carlo模拟得到了模型(1)的小样本性质。本文将利用文献〔5〕的一些结果来研究重复观测值的回归问题。
原理与方法
设在研究总体中随机地选出n个受试对象，分别对每一对象重复测量p次，得观测值(Xij，Yij)，i=1,2,…,n, j=1,2,…,p。现分析X与Y间的关系。
对上述重复观测数据，可建立如下半参数回归模型：
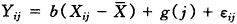
(2)
其中b为模型参数，主要反应了X对Y的影响。
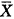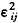=为X的平均数。g(j)为未知函数，主要反应了重复测量的效应。εij为随机误差，E(εij)=0，E()=σ2,且εij相互独立。, 百拇医药
沿用文献〔5〕中的方法，对模型(2)的参数进行估计。
1.把b看为已知时，g(j)的最小二乘估计为
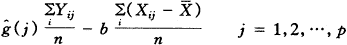
(3)
显然
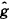(j)也为g(j)的一个邻近估计。2.把(3)式代入(2)后b的最小二乘估计为使
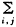(Yij-bXij-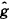(j))2最小的解。为了简便起见，作变换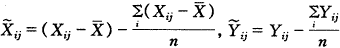，则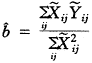, http://www.100md.com
(4)
事实上，(
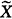ij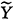，ij)为原始数据消除了自相关性后所得的序列。当假定εij服从N(0，σ2)时，由文献〔5〕结果，σ2的估计式为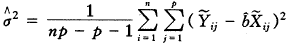：(5)
并且，
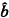的假设检验可用如下t统计量：, http://www.100md.com
(6)
总变异的分解
记
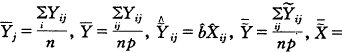
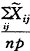。并注意到，有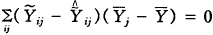：(7)
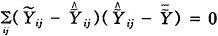
(8)
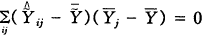
(9)
, 百拇医药
上面3个式子表明，
是相互独立的。而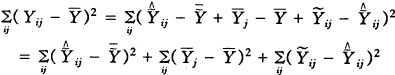(10)
事实上，对b进行最小二乘估计时，是拟合如下线性模型：
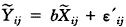
(11)
显然，ε′ij=εij+g(j)-
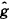(j)，由于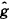(j)收敛与g(j)，因此，当N较大时，可假定ε′ij与εij同分布，即ε′ij也服从N(0，σ2)且相互独立。于是，在(10)式中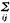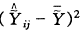，可解释为模型(2)中参数的回归平方和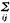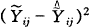；可解释为模型(2)的误差平方和；显然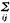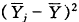，为重复观测所引起的变异。注意到(6)式中模型误差的自由度为np-p-1。于是对模型(1)的假设检验可用如下方差分析表：, 百拇医药
表1 模型(1)的方差分析表 变异来源
SS
v
MS
F
总
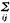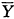(Yij-)2np
回归
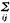
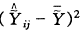
, 百拇医药
1
SSreg/vreg
MSreg/MSerr
重复
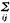
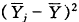
p
SSrep/vrep
MSrep/MSerr
误差
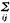
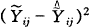
, 百拇医药
np-p-1
SSerr/verr
显然，在方差分析表中对回归系数的假设检验与(4)式中的t检验公式等价。并且根据方差分析中一般的自由度分解原理，文献〔5〕对误差的自由的模拟结果是可靠的。实 例
表2为某幼儿园9名幼儿连续3年的体重与身高数据。文献〔2〕曾分析得受试对象内残差相关是显著的。并且对体重与身高数据使用普通最小二乘法得到的回归系数
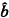的标准误将高估真实的标准误。于是在文献〔5〕中对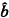的标准误进行调整后，得到对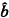的假设检验的t值为：6.2667，同时采用广义最小二乘法也得到t=9.9808，进一步说明了对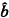的假设检验是显著的，即幼儿身高与体重有显著关系的结论。事实上，我们分别对1991年、1992年、1993年数据建立线性回归方程，则3个t值分别为：1.4744、0.6474、1.1136。也就是说，对此资料而言，如果剔除年龄因素的影响，幼儿的身高与体重应该是无关的。我们现用模型(2)来讨论表2中的数据，则有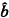：=0.2514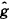，(1)=18.6116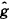，(2)=19.4563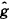，(3)=19.5611。对其半参数回归模型进行假设检验得到方差分析表(表3)。, http://www.100md.com
表2 某幼儿园幼儿的体重与身高 编号
观测日期
1991年
(6/7)
1992年
(25/5)
1993年
(24/5)
1
X(cm)
105.0
113.7
, 百拇医药 120.0
Y(kg)
16.3
18.7
19.7
2
X(cm)
102.5
110.3
117.0
Y(kg)
16.2
20.3
, 百拇医药
23.5
3
X(cm)
104.5
110.4
117.7
Y(kg)
15.81
18.4
20.4
4
X(cm)
109.8
, 百拇医药
117.1
124.4
Y(kg)
16.1
18.6
21.0
5
X(cm)
103.8
110.0
112.0
Y(kg)
17.0
, 百拇医药
19.0
18.55
6
X(cm)
106.0
113.7
120.7
Y(kg)
16.1
17.8
19.3
7
X(cm)
, 百拇医药
110.3
115.8
123.7
Y(kg)
20.3
24.3
27.9
8
X(cm)
103.0
110.5
116.2
Y(kg)
, 百拇医药
17.3
19.7
21.6
9
X(cm)
106.9
113.1
121.0
Y(kg)
17.0
18.7
19.1
表3 对表2数据拟合模型(2)的方差分析表 变异来源
, 百拇医药
SS
v
MS
F
P
总
198.90
27
回归
15.05
1
15.05
3.51
, 百拇医药 >0.05
重复
85.31
3
28.44
6.64
<0.01
误差
98.54
23
4.28
由表3可看出，对幼儿而言，如果剔除年龄因素的影响时，身高与体重是无关的，而对体重影响的主要因素为年龄因素。当仅使用公式(6)对
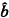进行假设检验得：t=1.8735，即为表3中回归因素的F值的平方根，与分别对3年的数据讨论得到的t值较为接近。讨 论, 百拇医药
1.分析幼儿身高与体重的关系应考虑年龄因素的影响。事实上就此资料而言，如果排除年龄因素的影响后，由于幼儿的体重变异远远大于身高的变异而掩盖了身高对体重的影响，幼儿的身高与体重是无关的。
2.对重复测量数据进行回归分析时，由于数据间的自相关性，一般的最小二乘法将失效。事实上，在文献〔2〕中无论是采用对标准误进行调整还是采用广义最小二乘法均得到了与实际资料所显示的信息不相符的结果。此实例的结果显示，半参数回归分析用于处理重复测量数据时的效果优于普通的最小二乘法和广义最小二乘法。
3.由方差分析表可看出，在文献〔5〕中对半参数回归模型的误差的小样本模拟结果是可靠的，并且我们应用半参数回归模型研究重复观测数据的回归问题取得了较好的结果，我们将进一步对在理论上对半参数回归的小样本性质进行研究，拓展半参数回归在医学数据处理中的应用领域。
*国家自然科学基金资助项目(39870691)
, http://www.100md.com
参考文献
1.陈希儒，王松桂.近代回归分析——原理方法及应用.第1版.合肥：安徽教育出版社，1987，91.
2.赵景波，李康.重复观测值线性回归分析及其在医学中的应用.中国卫生统计，1995，12(2)：18.
3.高集体，等.半参数回归模型研究的若干进展.应用概率统计，1994，10(1)：96.
4.洪圣岩.一类半参数模型的估计理论.中国科学(A辑)，1991，12(12)：1258.
5.王文昌，等.季节性时间序列资料预测的半参数回归模型.中国卫生统计，1997，14(6)：4., 百拇医药