综合效益影响因素的多层次分析*
作者：蔡辉 倪宗瓒
单位：蔡辉 南通医学院卫生系(226001); 倪宗瓒 华西医科大学卫生统计教研室(610041)
关键词：多层次模型；多因素分析；综合效益
中国卫生统计990402 【提 要】 目的 对全国12省34个县医院的综合效益影响因素进行分析。方法 应用多层次分析方法，从固定效应和随机效应的角度，经广义最小二乘迭代法(IGLS)估算各种参数。结果 经综合效益影响因素的筛选和分析，获得各因素对综合效益的影响层次、大小和方向等参数，同时探讨了多层次分析方法的应用条件和算法。结论 医院综合效益值可在省、县等不同层次受到不同的投入与产出因素的影响。
Multilevel Model Used in Analysis of Influence Factors of Comprehensive Benefit
, 百拇医药
Cai Hui,Department of Public Health,Nantong Medical College(266001)，Jiangsu,Ni Zongzan，Departent of Health Statisitcs,West China University of Medical Science,Chengdu
【Abstract】 Objective To analyze the influence factors of Comprehensive benefit of 34 County hospitals in 12 provinces in China.Methods With the method of IGLS in multilevel model the various parameters of fixed and random effect were calculated.Results By selection and analysis of influence factors of comprehensive benefit the affecting level，strength and direction of influence factors were determined.At the same time the application conditions and calculation method of multilevel model were dicussed.Conclusion Comprehensive benefit of hospital could be affected by some input and output factors in province and county level.
, 百拇医药
【Key words】 Mulitlevel model Multivariable alnalysis Comprehensive beneflit
在卫生管理工作中，综合效益评价是一项重要任务，其评价对象或评价指标也呈多层次结构，对于这类数据，人们往往用一般的方法或模型予以分析处理，忽视了数据的多层次结构特征，使分析过程不够充分，分析结论不够全面。本文拟用多层次(multilevel)分析模型〔1，2〕，在对全国12个省、34个县医院抽样调查的基础上，针对综合效益及其不同层次的影响因素进行分析处理，获得较为客观和丰富的结论。
一、计算方法
设一组数据有如下结构：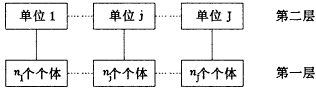
图1 两层次数据结构模型
, http://www.100md.com
在此结构下，因变量Y的变异可分为两部分，单位间的变异和个体间的变异。若某自变量X对Y产生影响，则各单位内的回归线就会发生变化。若这些直线的截距有统计学意义，表示当X＝0时，各单位间的Y值不同；若这些直线的斜率有统计学意义，则表示随着X的变化，各单位Y的变化速率不一致。
若用这类资料建立一般回归方程：
Y=a+bx+ε
则得不到Y在各单位间的变异，因此，可建立回归方程：
Yij=β0jx0+β1jxij+eij
上式为在第j个单位下nj个个体的回归方程，Yij为第j个单位中第i个个体的Y值，β0j为截距，x0≡1，β1j为斜率，eij为个体水平的随机误差。
, http://www.100md.com
一般来说，β0j和β1j在第二层各单位间是可变的，也即为随机变量，其变异可用下式表示：
β0j=γ00+μ0j
β1j=γ10十μ1j
式中γ00表示当xij＝0时Y的均数，γ10是
j随
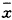j变化的斜率均值，μ0j和μ1j表示各单位间β0j和β1j的随机误差。
, http://www.100md.com
将上述三个方程合并后得：
Yij=γ00x0+γ10x1ij+(μ0jx0+μ1jx1ij+eijx0)
方程中前二项为固定项，其系数为固定系数，γ00为平均截距，γ10为平均斜率，括号中的各项为随机项。
因为随机项的变异可用随机参数的估计来描述〔3〕，所以
设 Yij′＝Yij-(γ00x0+γ10x1ij)
, 百拇医药
则 Var(Yij′)=σu02x02+2σu0u1x0x1ij+σu12x1ij2+σe2x02=σu02+2σu0u1x1ij+σu12x1ij2+σe2
上式中σu02、σu0u1、σu12、σe2为待估参数。σu02是指x=0时各单位j间的方差(截距的方差)，σu12为各单位y随x变化的斜率方差，σe2是单位内剩余误差的方差，σu0u1是上述截距与斜率间的协方差。这些参数可用广义最小二乘法经迭代算出。
, 百拇医药
二、结果与分析
本文应用MLn软件，分别计算我国1989年～1992年间部分省份县级医院的投入产出资料在省、县与年之间的内部相关性(表1)〔4〕，得r省=0.3037，r县=0.7354，据此认为该资料可进行多层次分析。
表1 各层次间内部相关性分析
r
省
0.002084
0.004777
, http://www.100md.com
0.3037
县
0.005102
0.001836
0.7354
通过多层次分析，可得到与省、县和年份等各级水平有关的投入(x)和产出(y)指标(表2～4)。表2 省级投入指标的两层次分析*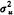
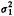
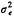
γ00
, http://www.100md.com
γ10
x6
6.25
9.53
4.54
528.3
-46.22
x11
2.86
6.29
4.67
497.4
, http://www.100md.com
-
x14
10.99
10.97
4.38
477.3
33.96
*表内数据除以1000即为原值表3 省级产出指标的两层次分析*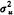
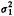
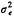
, 百拇医药
γ00
γ10
x7
3.72
9.28
4.16
512.5
-23.56
x9
2.60
3.93
4.52
, 百拇医药
462.2
74.22
x12
11.04
32.75
3.94
442.0
87.93
*表内数据除以1000即为原值表4 县级产出指标的两层次分析*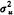
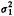
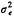
, 百拇医药
γ00
γ10
x6
21.32
67.98
1.38
508.1
-19.28
x7
11.38
14.96
1.72
, 百拇医药
503.6
-30.86
x11
7.93
12.42
1.54
426.1
117.30
x14
15.31
25.96
1.52
, http://www.100md.com
452.1
63.60
*表内数据除以1000即为原值 由表2可知，若不考虑x6的影响时，省级的平均效益值Z为0.5283，而在x6的影响下，各省间的Z值也不尽相同，其方差为0.00625(P<0.05)，而x6与Z值之间的回归系数为-0.04622，提示这两个因素在省级水平呈负相关；x11在省级水平的各种方差都小于相应的标准误，可认为x11对各省的效益值无影响；x14是指医院卫生事业费，该指标在各省之间也不相等，在排除该因素的影响时，省级平均效益值为0.4773，但是，由于x14的影响，各省的平均效益值也不相同。值得注意的是，x14与Z值间呈正相关(b＝0.03396，SEb=0.002469)，提示只要投入恰当，是可以提高效益的。
, http://www.100md.com
表3提示，就省级水平总体而言，随着y9的增加，省级平均效益值也随之增大(回归系数为0.074)，但各省的效益值并不一致，这种差异由y7和y12所致，其离散度分别为0.00372和0.01104，同时本研究还提示这两个指标对各省平均效益值增长速度(斜率)也有影响。
总之，与省级综合效益有关的5个指标中，多数都可影响到各省平均效益值变动的截距和斜率，但对于省级总效益来说，与x6呈负相关、y9呈正相关。
表4反映了与县级水平有关的投入指标，这些指标都可影响各县平均效益值变化的截距，其中仅x6对各县平均效益的变化速率产生影响；若将各县作为一个总体来看，上述四个指标对其平均效益发展的截距(起始水平)都有作用，而就平均效益的发展速度而言，与x11和x14呈正相关(P<0.01和P<0.10)。
, 百拇医药
在县级产出指标中，y10、y12、y16、y18和y20可影响各县综合效益值Z发展起点(截距)的高低，其中y12对各县Z值发展的速率也有影响，其方差为0.04750(P<0.05)。
三、讨论
多层次分析模型是在Ⅱ型方差分析的基础上建立起来的。早在十八世纪末，人们就对多层次(即嵌套设计)资料产生兴趣，因为这种资料若用一般的回归方法处理，必然不能将高层次的信息分离出来。本世纪中叶，已有很多学者研究解决这类问题的方法，如Eisenhart和Henderson通过对动物饲养实验结果的处理，促进了方差成分分析法的发展；Hartley和Rao于1967年使用Fisher计分和Newton—Raphson迭代法，首次提出随机效应模型的最大似然估计方法，到七十年代，由于农业和生物学的需要，多层次分析法在应用的同时，方法学上又有很大的发展并不断完善，八十年代初已应用于教育学〔5〕。与简单的回归分析相比，在多层次分析中，因素对高层次影响效应的估计更具优势。
, 百拇医药
1.分析结果：在评价指标体系中，对县级效益值的影响因素有x6、x7、x11、x14、y10、y12、y16、y18和y20，这些指标都与县级平均效益值发展的截距有关，它们中的x11、x14和y18，还同时影响到县级平均效益值发展的速度，而各县效益值发展的截距不相同，也受上述四个投入指标和y12的影响，各县效益值变化速度的差异主要由x6、x14、y12三个因素造成，此中尤以x6的作用为大；对省级平均效益值有影响的因素为x6、x14、y7、y9和y12，从总体上看，这五个指标都关系到省级综合效益值发展起点(截距)的高低，其中x14和y9对其发展速度产生影响，各省的效益发展也不平衡，x6、x14、y12对每个省综合效益发展的初值(截距)具有影响，其中y12还与各省的综合效益的发展速率有关。
, 百拇医药
2.模型结构：多层次分析可分为方差成分模型(variance components model)和随机系数回归模型(random coefficient regression model)，前者是指在第二层次各单位间，因变量变化的斜率是固定的，仅截距有所不同；后者系指上述两方面都有变化。通过方差成分分析模型可知，若各单位间变异占总变异的比例r>10%，应考虑在Y的变异中，有一部分可由单位间差异(第二层次)来解释，可用多层次分析；若r≤10%，只考虑一个层次，用普通的回归分析即可。用何种方法分析，主要决定于内部相关性(introcorrelation)的大小，其计算公式为：
r=σu2/(σu2+σe2)
3.效应分类：多层次分析可分为固定效应和随机效应两部分。固定效应主要用平均数描述，如因变量的平均水平、因变量随某个自变量变化的平均变化强度；随机效应主要以方差或协方差来描述，如斜率和截距的方差等。这些统计量的估计有两种方法：广义最小二乘迭代法(IGLS)和条件广义最小二乘迭代法(RIGLS)，前者为一致性估计，后者为无偏估计。有时用IGLS迭代不收敛时，可用RIGLS来估算。
, http://www.100md.com
4.样本含量：多层次分析对样本含量的要求较高。在两层次分析中，如果需要估计第二层的参数超过三个时，则第二层的单位数至少应有50个，否则会出现迭代不收敛或参数估计为0的现象。在本研究中，因仅调查了12个省、34个县，因此在分析时也产生不收敛或参数估计不出的情形，同时因样本含量偏小，一些参数也未达到显著性水平(α=0.05)，但此时若在固定项中去除无统计学意义的变量，同时若r在25%以上时，也能得到较好的分析效果。
*国家自然科学基金资助项目(项目编号39500127)
参考文献
1.Goldstein H.:Efficient Statistical Modeling of Longitudinal Data.Annals of Human Biology，1986，13，129～141.
2.Goldstein，H:Multilevel Statistical Models.London：Edward Arnold.1995.
3.G.Woodhouse Multilevel Modeling Applications-A Guide for Users of MLn.Institute of Education.University of London.1996，59.
4.李晓松，倪宗瓒.两水平方差成分模型与线性回归模型关系的探讨.中国卫生统计，1999，16(1)：14～16.
5.Nicholas T.Longford:Random Coefficient Models.Oxford University Press lnc.New York，1993., http://www.100md.com
单位：蔡辉 南通医学院卫生系(226001); 倪宗瓒 华西医科大学卫生统计教研室(610041)
关键词：多层次模型；多因素分析；综合效益
中国卫生统计990402 【提 要】 目的 对全国12省34个县医院的综合效益影响因素进行分析。方法 应用多层次分析方法，从固定效应和随机效应的角度，经广义最小二乘迭代法(IGLS)估算各种参数。结果 经综合效益影响因素的筛选和分析，获得各因素对综合效益的影响层次、大小和方向等参数，同时探讨了多层次分析方法的应用条件和算法。结论 医院综合效益值可在省、县等不同层次受到不同的投入与产出因素的影响。
Multilevel Model Used in Analysis of Influence Factors of Comprehensive Benefit
, 百拇医药
Cai Hui,Department of Public Health,Nantong Medical College(266001)，Jiangsu,Ni Zongzan，Departent of Health Statisitcs,West China University of Medical Science,Chengdu
【Abstract】 Objective To analyze the influence factors of Comprehensive benefit of 34 County hospitals in 12 provinces in China.Methods With the method of IGLS in multilevel model the various parameters of fixed and random effect were calculated.Results By selection and analysis of influence factors of comprehensive benefit the affecting level，strength and direction of influence factors were determined.At the same time the application conditions and calculation method of multilevel model were dicussed.Conclusion Comprehensive benefit of hospital could be affected by some input and output factors in province and county level.
, 百拇医药
【Key words】 Mulitlevel model Multivariable alnalysis Comprehensive beneflit
在卫生管理工作中，综合效益评价是一项重要任务，其评价对象或评价指标也呈多层次结构，对于这类数据，人们往往用一般的方法或模型予以分析处理，忽视了数据的多层次结构特征，使分析过程不够充分，分析结论不够全面。本文拟用多层次(multilevel)分析模型〔1，2〕，在对全国12个省、34个县医院抽样调查的基础上，针对综合效益及其不同层次的影响因素进行分析处理，获得较为客观和丰富的结论。
一、计算方法
设一组数据有如下结构：
图1 两层次数据结构模型
, http://www.100md.com
在此结构下，因变量Y的变异可分为两部分，单位间的变异和个体间的变异。若某自变量X对Y产生影响，则各单位内的回归线就会发生变化。若这些直线的截距有统计学意义，表示当X＝0时，各单位间的Y值不同；若这些直线的斜率有统计学意义，则表示随着X的变化，各单位Y的变化速率不一致。
若用这类资料建立一般回归方程：
Y=a+bx+ε
则得不到Y在各单位间的变异，因此，可建立回归方程：
Yij=β0jx0+β1jxij+eij
上式为在第j个单位下nj个个体的回归方程，Yij为第j个单位中第i个个体的Y值，β0j为截距，x0≡1，β1j为斜率，eij为个体水平的随机误差。
, http://www.100md.com
一般来说，β0j和β1j在第二层各单位间是可变的，也即为随机变量，其变异可用下式表示：
β0j=γ00+μ0j
β1j=γ10十μ1j
式中γ00表示当xij＝0时Y的均数，γ10是
j随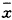j变化的斜率均值，μ0j和μ1j表示各单位间β0j和β1j的随机误差。, http://www.100md.com
将上述三个方程合并后得：
Yij=γ00x0+γ10x1ij+(μ0jx0+μ1jx1ij+eijx0)
方程中前二项为固定项，其系数为固定系数，γ00为平均截距，γ10为平均斜率，括号中的各项为随机项。
因为随机项的变异可用随机参数的估计来描述〔3〕，所以
设 Yij′＝Yij-(γ00x0+γ10x1ij)
, 百拇医药
则 Var(Yij′)=σu02x02+2σu0u1x0x1ij+σu12x1ij2+σe2x02=σu02+2σu0u1x1ij+σu12x1ij2+σe2
上式中σu02、σu0u1、σu12、σe2为待估参数。σu02是指x=0时各单位
j间的方差(截距的方差)，σu12为各单位y随x变化的斜率方差，σe2是单位内剩余误差的方差，σu0u1是上述截距与斜率间的协方差。这些参数可用广义最小二乘法经迭代算出。, 百拇医药
二、结果与分析
本文应用MLn软件，分别计算我国1989年～1992年间部分省份县级医院的投入产出资料在省、县与年之间的内部相关性(表1)〔4〕，得r省=0.3037，r县=0.7354，据此认为该资料可进行多层次分析。
表1 各层次间内部相关性分析
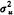
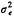
r
省
0.002084
0.004777
, http://www.100md.com
0.3037
县
0.005102
0.001836
0.7354
通过多层次分析，可得到与省、县和年份等各级水平有关的投入(x)和产出(y)指标(表2～4)。表2 省级投入指标的两层次分析*
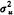
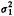
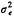
γ00
, http://www.100md.com
γ10
x6
6.25
9.53
4.54
528.3
-46.22
x11
2.86
6.29
4.67
497.4
, http://www.100md.com
-
x14
10.99
10.97
4.38
477.3
33.96
*表内数据除以1000即为原值表3 省级产出指标的两层次分析*
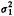
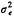
, 百拇医药
γ00
γ10
x7
3.72
9.28
4.16
512.5
-23.56
x9
2.60
3.93
4.52
, 百拇医药
462.2
74.22
x12
11.04
32.75
3.94
442.0
87.93
*表内数据除以1000即为原值表4 县级产出指标的两层次分析*
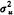
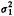
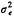
, 百拇医药
γ00
γ10
x6
21.32
67.98
1.38
508.1
-19.28
x7
11.38
14.96
1.72
, 百拇医药
503.6
-30.86
x11
7.93
12.42
1.54
426.1
117.30
x14
15.31
25.96
1.52
, http://www.100md.com
452.1
63.60
*表内数据除以1000即为原值 由表2可知，若不考虑x6的影响时，省级的平均效益值Z为0.5283，而在x6的影响下，各省间的Z值也不尽相同，其方差为0.00625(P<0.05)，而x6与Z值之间的回归系数为-0.04622，提示这两个因素在省级水平呈负相关；x11在省级水平的各种方差都小于相应的标准误，可认为x11对各省的效益值无影响；x14是指医院卫生事业费，该指标在各省之间也不相等，在排除该因素的影响时，省级平均效益值为0.4773，但是，由于x14的影响，各省的平均效益值也不相同。值得注意的是，x14与Z值间呈正相关(b＝0.03396，SEb=0.002469)，提示只要投入恰当，是可以提高效益的。
, http://www.100md.com
表3提示，就省级水平总体而言，随着y9的增加，省级平均效益值也随之增大(回归系数为0.074)，但各省的效益值并不一致，这种差异由y7和y12所致，其离散度分别为0.00372和0.01104，同时本研究还提示这两个指标对各省平均效益值增长速度(斜率)也有影响。
总之，与省级综合效益有关的5个指标中，多数都可影响到各省平均效益值变动的截距和斜率，但对于省级总效益来说，与x6呈负相关、y9呈正相关。
表4反映了与县级水平有关的投入指标，这些指标都可影响各县平均效益值变化的截距，其中仅x6对各县平均效益的变化速率产生影响；若将各县作为一个总体来看，上述四个指标对其平均效益发展的截距(起始水平)都有作用，而就平均效益的发展速度而言，与x11和x14呈正相关(P<0.01和P<0.10)。
, 百拇医药
在县级产出指标中，y10、y12、y16、y18和y20可影响各县综合效益值Z发展起点(截距)的高低，其中y12对各县Z值发展的速率也有影响，其方差为0.04750(P<0.05)。
三、讨论
多层次分析模型是在Ⅱ型方差分析的基础上建立起来的。早在十八世纪末，人们就对多层次(即嵌套设计)资料产生兴趣，因为这种资料若用一般的回归方法处理，必然不能将高层次的信息分离出来。本世纪中叶，已有很多学者研究解决这类问题的方法，如Eisenhart和Henderson通过对动物饲养实验结果的处理，促进了方差成分分析法的发展；Hartley和Rao于1967年使用Fisher计分和Newton—Raphson迭代法，首次提出随机效应模型的最大似然估计方法，到七十年代，由于农业和生物学的需要，多层次分析法在应用的同时，方法学上又有很大的发展并不断完善，八十年代初已应用于教育学〔5〕。与简单的回归分析相比，在多层次分析中，因素对高层次影响效应的估计更具优势。
, 百拇医药
1.分析结果：在评价指标体系中，对县级效益值的影响因素有x6、x7、x11、x14、y10、y12、y16、y18和y20，这些指标都与县级平均效益值发展的截距有关，它们中的x11、x14和y18，还同时影响到县级平均效益值发展的速度，而各县效益值发展的截距不相同，也受上述四个投入指标和y12的影响，各县效益值变化速度的差异主要由x6、x14、y12三个因素造成，此中尤以x6的作用为大；对省级平均效益值有影响的因素为x6、x14、y7、y9和y12，从总体上看，这五个指标都关系到省级综合效益值发展起点(截距)的高低，其中x14和y9对其发展速度产生影响，各省的效益发展也不平衡，x6、x14、y12对每个省综合效益发展的初值(截距)具有影响，其中y12还与各省的综合效益的发展速率有关。
, 百拇医药
2.模型结构：多层次分析可分为方差成分模型(variance components model)和随机系数回归模型(random coefficient regression model)，前者是指在第二层次各单位间，因变量变化的斜率是固定的，仅截距有所不同；后者系指上述两方面都有变化。通过方差成分分析模型可知，若各单位间变异占总变异的比例r>10%，应考虑在Y的变异中，有一部分可由单位间差异(第二层次)来解释，可用多层次分析；若r≤10%，只考虑一个层次，用普通的回归分析即可。用何种方法分析，主要决定于内部相关性(introcorrelation)的大小，其计算公式为：
r=σu2/(σu2+σe2)
3.效应分类：多层次分析可分为固定效应和随机效应两部分。固定效应主要用平均数描述，如因变量的平均水平、因变量随某个自变量变化的平均变化强度；随机效应主要以方差或协方差来描述，如斜率和截距的方差等。这些统计量的估计有两种方法：广义最小二乘迭代法(IGLS)和条件广义最小二乘迭代法(RIGLS)，前者为一致性估计，后者为无偏估计。有时用IGLS迭代不收敛时，可用RIGLS来估算。
, http://www.100md.com
4.样本含量：多层次分析对样本含量的要求较高。在两层次分析中，如果需要估计第二层的参数超过三个时，则第二层的单位数至少应有50个，否则会出现迭代不收敛或参数估计为0的现象。在本研究中，因仅调查了12个省、34个县，因此在分析时也产生不收敛或参数估计不出的情形，同时因样本含量偏小，一些参数也未达到显著性水平(α=0.05)，但此时若在固定项中去除无统计学意义的变量，同时若r在25%以上时，也能得到较好的分析效果。
*国家自然科学基金资助项目(项目编号39500127)
参考文献
1.Goldstein H.:Efficient Statistical Modeling of Longitudinal Data.Annals of Human Biology，1986，13，129～141.
2.Goldstein，H:Multilevel Statistical Models.London：Edward Arnold.1995.
3.G.Woodhouse Multilevel Modeling Applications-A Guide for Users of MLn.Institute of Education.University of London.1996，59.
4.李晓松，倪宗瓒.两水平方差成分模型与线性回归模型关系的探讨.中国卫生统计，1999，16(1)：14～16.
5.Nicholas T.Longford:Random Coefficient Models.Oxford University Press lnc.New York，1993., http://www.100md.com