死因别危险度联合分析模型饲喂乳杆菌对雏鸡盲肠8种正常菌群定植的影响
作者:李克 俞顺章
单位:李克 汕头大学医学院(515031); 俞顺章 上海医科大学(200032)
关键词:
中国卫生统计990423 在临床生存试验研究和队列调查中,常需研究某(些)暴露与一种以上疾病间的关系,这时,常规分析通常按所研究疾病进行分别分析(Separate Analysis),估计暴露对每种疾病的回归效应,并假定暴露仅与分析的疾病有关(Breslow,1987)〔1〕。很显然,一方面,其前提和假设均不够完善,首先,暴露可能与一种以上的研究疾病有关,其次,个体在随访期间持续地暴露于多种死亡危险,并面临它们的互相竞争。即“竞争性危险度”(Competing Risks)〔2〕。另一方面,有缺陷的假设导致了分析方法的片面性。例如,不能采用正规的统计方法对暴露的死因别回归效应之间的差异进行检验,也不能认识和分析研究疾病间存在的相互关系。近年来关于这类问题进行了死因别危险度函数估计理论〔3〕方面的探讨,在理论上,解决了对研究疾病进行联合分析的问题。在应用方面,也解决了使用通用计算机软件进行模型拟合和参数估计的问题〔4,5〕。鉴于多疾病联合分析的理论和应用具有广泛的实际意义,本文利用一个研究实例,对其原理、方法和应用进行了较为详细的阐述。
, http://www.100md.com
基本原理
1.生存数据包括:失效时间(T≥1),可以是右截尾数据;失效类型J∈{1,2,…,m),T截尾时,失效类型是未知的;回归变量x=(x1,…,xp),x可以是时间协变量,即x=x(t)。T可为个体死亡时的年龄,J用来指定研究疾病的类型,x为协方差矩阵(如人口学特征、暴露剂量及混杂分层变量等)。
2.死因别危险度函数估计理论:按研究的疾病类型进行分层,并使用Cox回归和Poisson回归方法〔3,4〕。应用该理论可以进行死因别回归系数的推断和死因类型间相对危险度的分析,按Kalbfleisch和Prentice〔3〕提出的方法,可将这种模型的似然函数表述为特定疾病类型项之乘积,对于两种模型的参数似然估计是相同的。
在此利用一般生存数据的Cox回归模型检验和估计λj(t;x),j=1,…,m。死因别危险度模型为〔6,7〕:
, 百拇医药
λj(t;x)=λ0j(t)exp(xβj)
(1)
λ0j()≥0,为未知的基准危险度,βj为死因别回归系数列矩阵,对βj的检验实际上就是关于暴露因素对每个类型的回归效应是否相同。βj估计可用Holt〔7〕的偏似然方法: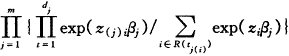
(2)
在此,tj(i)(i=1,…,dj)表示j个类型的dj个失效时间,zj(i)表示有关的回归变量,R(tj(i))为恰好在tj(i)之前处于危险的对象集,zj(i)为tj(i)时的zi。当没有回归变量存在时,Kaplan-Meier方法可用于估计λj(t)〔8〕。
, 百拇医药
3.模型拟合:为利用标准程序和软件进行拟合,根据Larson和Lunn〔5,9〕的描述,采用了数据复制的方法,设有三种研究疾病类型,可分别取值1,2,3,例如,某个体在时间t失效,失效类型为1,δi=1,数据将复制2次,如表1。
表1 竞争性危险度Cox回归模型的数据布局 对象
反应δi
状态
失效类型
协变量
i
ti
1
, 百拇医药
1
xi,δixi
i
ti
0
2
xi,δixi
i
ti
0
3
xi,δixi
, http://www.100md.com
如果个体为截尾数据,数据也进入3次,状态均为0。对于每一种类型显示一次截尾观察,协变量x也扩大,增加失效类型因子与x的交互作用项。资料与方法
应用的例子为某橡胶厂前瞻性队列23年的随访资料(1973~1995),研究的变量包括生活习惯、家庭环境、经济状况、职业因素、及个人人口学特征等,职业因素为5种橡胶化合物的暴露。根据以前分别分析的结果〔10〕,将研究疾病归为3种疾病类型,即肺癌、肠癌和胰腺癌、及缺血性心脏病和脑血管病。旨在研究①5种橡胶化合物的不同类型疾病危险度之间有无统计学差异;②恶性肿瘤与心脑血管疾病死因间的相互关系;③恶性肿瘤与心脑血管疾病间是否存在竞争性死亡等问题。
结果与分析
1.三种疾病类型间相互关系的描述
按死因类型分层,拟合Cox比例危险度的简单模型(没有包括其他协变量)。图1显示三种死因类型的生存曲线,表明55岁以前,三种疾病的死亡危险度均是很小的,曲线间互相交叉和重叠。50岁以后,生存率开始下降,以心、脑血管疾病最为明显。类型别死亡危险度是否随生存时期呈平滑的趋势(即按比例升高或下降),是通过将类型层变量拟造为时间协变量来检验的。如果包括所有年龄,比例危险度的假设检验统计量P值为临界水平(似然比=3.76,自由度为1,P=0.052)。如果排除小于50岁的生存年龄,显示约2%死因别危险度随生存年龄稍有上升,但比例危险度假设成立(似然比=1.95,自由度为1,P=0.163)。
, http://www.100md.com
图1 三种死因别生存率曲线
将死因类型变量指定为因子水平,进行简单模型的拟合,可以估计2个参数。肠癌和胰腺癌相对于肺癌的死亡危险度约40%,而心脑血管疾病死亡危险度约为肺癌的3倍,并均有统计意义。
2.慢性疾病史对三类死因的危险度
表2显示,在随访开始时记录有高血压疾病史的个体中,二类恶性肿瘤死亡危险度下降,心脑血管疾病死亡危险度增高,死因别危险度间的差别显著,既往心脏病史对死因别危险度没有明显的效应。慢性支气管炎在此作为参比,在死因别之间的危险度没有显著性差别。
表2 随访开始时疾病史的死因别危险度分析 疾病史
肺癌
肠癌和胰腺癌
, 百拇医药
心脑血管疾病
一致性检验
β
RR
β
RR
β
RR
似然比*
P值
高血压
-0.28
0.75
, http://www.100md.com
-0.26
0.77
0.78
2.20**
7.07
0.03
心脏病
0.16
1.18
-0.78
0.46
0.70
2.00**
, http://www.100md.com
3.91
0.14
慢性支气管炎
-0.06
0.94
0.84
2.31
-0.45
0.64
5.65
0.06
*自由度为2的似然比检验,**95%可信限不包括1。 3.职业暴露的死因别回归系数
, 百拇医药
将性别、疾病类型、吸烟、经济状态、血压、胆固醇等变量作为分层因素,拟合职业暴露主效应模型,并指定该模型为零模型。然后,将职业暴露变量与疾病类型因子的交互作用项引入模型,拟合并进行死因别回归系数的一致性检验。职业暴露为5种橡胶化合物,为指示变量形式。拟合结果见表3。亚硝胺暴露在三种死因类型间的危险度差别有统计意义。其中,亚硝胺暴露对于2种恶性肿瘤类型有明显的正性效应,相对危险度分别为2.25和2.92,肺癌危险度增高有统计意义。对于心血管疾病,亚硝胺暴露相对危险为1.02。其他4种橡胶化合物暴露的死因别危险度之间没有显著性差别。
表3 5种橡胶化合物死因别回归系数(生存年龄≥50岁) 职业暴露
肺 癌
肠癌和胰腺癌
心血管疾病
一致性检验
, 百拇医药
β
SE
RR
β
SE
RR
β
SE
RR
似然比*
P值
亚硝胺
0.81
, 百拇医药
0.32
2.25**
1.07
0.56
2.92
0.02
0.19
1.02
6.71
0.04
芳香胺
0.56
0.34
, 百拇医药
1.75
0.41
0.52
1.51
-0.07
0.18
0.93
3.22
0.20
溶剂
-0.42
0.42
0.66
, http://www.100md.com
0.18
0.52
1.20
0.03
0.19
1.03
1.15
0.56
滑石
0.02
0.33
1.02
-0.26
, http://www.100md.com
0.54
0.77
0.05
0.20
1.05
0.30
0.86
碳黑
0.24
0.31
1.26
0.74
0.51
, 百拇医药
2.10
-0.08
0.18
0.92
2.82
0.24
*自由度为2的似然比检验,**95%可信限不包括1。讨 论
对不同死因进行联合分析的方法并不需要死因间竞争性危险度相互独立的假设〔4,5〕,见式2,模型的似然函数为疾病类型项之乘积〔3〕。相对死因分别分析而言,联合分析的优点在于:
(1)可以估计疾病类型别危险度的差别,即进行疾病类型间相互关系的研究;
, 百拇医药
(2)在模型中估计各变量死因别的回归效应,分析那些效应是疾病类型共有的,那些是特定类型的;
(3)可以对疾病类型别的危险度差别进行正式的显著性检验,从而证明在分别分析中的结果;
(4)在联合分析模型中,不同疾病类型的死亡数合计大于分别分析中的死亡数,可使统计效率增高。
应用联合模型对5种橡胶化合物的死因别回归系数进行检验,只有亚硝胺暴露的危险度在三个死因类型间有显著性差别。其中,肺癌危险度显著增高。
三种疾病类型中,死亡危险度从高至低依次为心脑血管疾病、肺癌、以及肠和胰腺癌。心脑血管疾病死亡危险度显著地高于其他两类恶性肿瘤。由此考虑了心脑血管疾病与两类恶性肿瘤之间的相互关系。在此,不是认为心、脑血管疾病有预防恶性肿瘤的作用,而是认为它作为一种致死性疾病,与恶性肿瘤产生了竞争性死亡。于是,将既往患有高血压病史和心脏病史作为指示变量,应用比例危险度模型,估计死因别危险度。结果正如所预料的,在对多种混杂因子进行调整后,既往病史特别是高血压疾病史的心脑血管疾病死亡危险度增加,而其他两类恶性肿瘤死亡危险度下降,之间差别有统计学显著性。如果去除心脑血管疾病死因,剩下的两种恶性肿瘤的死亡危险度可能会发生很大变化。这是竞争性危险度分析中的焦点问题〔6〕。然而,已经证明,去死因的失效概率从(T,J,x)类型的资料中不能估计,这不是统计学的问题,而是生物学问题〔6〕。在生物学上,可考虑仅有一种方法移去心脑血管疾病死因,即假定有某种治疗药物能够控制和预防心脑血管疾病的死亡,延长其生命。这样在其他回归变量(x)效应不变情况下,恶性肿瘤的死亡概率可能会发生变化,应该增加。另一方面,概率可能又会受到该药物潜在的对两类恶性肿瘤效应的影响。
, http://www.100md.com
参考文献
1.Breslow NE,Day NE.Statistical methods in cancer research.VolⅡ.The design and analysis of cohort studies.Lyon:IARC,1987.
2.Chiang C L.Competing risks in mortality analysis.Annu Rev Health 1991,12:281.
3.Kalbfleish J D,Prentice R L.The statistical analysis of failure time data.New York:Wiley,1980,321.
4.Pierce D A,Preston D L Joint analysis of site-specific cancer risks for the Atomic Bomb Survivors.Radia Res,1993,134:134.
, 百拇医药
5.Lunn M,McNeil D.Applying Cox regression to competing risks.Biometrics.1995,51:524.
6.Prentice RL,Breslow NE.Retrospective studies and failure time models.Biometrika.1978,65:153.
7.Holt J D.Competing risk analysis with special reference to matched pair experiments.Biometrica.1978,65:159.
8.Aalen O.Nonparametric inference in connection with multiple decrement models.Scand J Stat,1976,3:15.
, 百拇医药
9.Larson MG.Covariate analysis of competing-risks data with Log linear models.Biometrics,1984,40:459.
中国微生态学杂志 1999年第1期第11卷 论著
饲喂乳杆菌对雏鸡盲肠8种正常菌群定植的影响
作者:刘永杰 赵艳兵 何梦辉 何昭阳
单位:刘永杰 赵艳兵 何梦辉 何昭阳 吉林农业大学动科系 长春 130118
关键词:乳杆菌;盲肠;正常菌群, 百拇医药
单位:李克 汕头大学医学院(515031); 俞顺章 上海医科大学(200032)
关键词:
中国卫生统计990423 在临床生存试验研究和队列调查中,常需研究某(些)暴露与一种以上疾病间的关系,这时,常规分析通常按所研究疾病进行分别分析(Separate Analysis),估计暴露对每种疾病的回归效应,并假定暴露仅与分析的疾病有关(Breslow,1987)〔1〕。很显然,一方面,其前提和假设均不够完善,首先,暴露可能与一种以上的研究疾病有关,其次,个体在随访期间持续地暴露于多种死亡危险,并面临它们的互相竞争。即“竞争性危险度”(Competing Risks)〔2〕。另一方面,有缺陷的假设导致了分析方法的片面性。例如,不能采用正规的统计方法对暴露的死因别回归效应之间的差异进行检验,也不能认识和分析研究疾病间存在的相互关系。近年来关于这类问题进行了死因别危险度函数估计理论〔3〕方面的探讨,在理论上,解决了对研究疾病进行联合分析的问题。在应用方面,也解决了使用通用计算机软件进行模型拟合和参数估计的问题〔4,5〕。鉴于多疾病联合分析的理论和应用具有广泛的实际意义,本文利用一个研究实例,对其原理、方法和应用进行了较为详细的阐述。
, http://www.100md.com
基本原理
1.生存数据包括:失效时间(T≥1),可以是右截尾数据;失效类型J∈{1,2,…,m),T截尾时,失效类型是未知的;回归变量x=(x1,…,xp),x可以是时间协变量,即x=x(t)。T可为个体死亡时的年龄,J用来指定研究疾病的类型,x为协方差矩阵(如人口学特征、暴露剂量及混杂分层变量等)。
2.死因别危险度函数估计理论:按研究的疾病类型进行分层,并使用Cox回归和Poisson回归方法〔3,4〕。应用该理论可以进行死因别回归系数的推断和死因类型间相对危险度的分析,按Kalbfleisch和Prentice〔3〕提出的方法,可将这种模型的似然函数表述为特定疾病类型项之乘积,对于两种模型的参数似然估计是相同的。
在此利用一般生存数据的Cox回归模型检验和估计λj(t;x),j=1,…,m。死因别危险度模型为〔6,7〕:
, 百拇医药
λj(t;x)=λ0j(t)exp(xβj)
(1)
λ0j()≥0,为未知的基准危险度,βj为死因别回归系数列矩阵,对βj的检验实际上就是关于暴露因素对每个类型的回归效应是否相同。βj估计可用Holt〔7〕的偏似然方法:
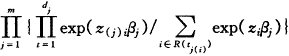
(2)
在此,tj(i)(i=1,…,dj)表示j个类型的dj个失效时间,zj(i)表示有关的回归变量,R(tj(i))为恰好在tj(i)之前处于危险的对象集,zj(i)为tj(i)时的zi。当没有回归变量存在时,Kaplan-Meier方法可用于估计λj(t)〔8〕。
, 百拇医药
3.模型拟合:为利用标准程序和软件进行拟合,根据Larson和Lunn〔5,9〕的描述,采用了数据复制的方法,设有三种研究疾病类型,可分别取值1,2,3,例如,某个体在时间t失效,失效类型为1,δi=1,数据将复制2次,如表1。
表1 竞争性危险度Cox回归模型的数据布局 对象
反应δi
状态
失效类型
协变量
i
ti
1
, 百拇医药
1
xi,δixi
i
ti
0
2
xi,δixi
i
ti
0
3
xi,δixi
, http://www.100md.com
如果个体为截尾数据,数据也进入3次,状态均为0。对于每一种类型显示一次截尾观察,协变量x也扩大,增加失效类型因子与x的交互作用项。资料与方法
应用的例子为某橡胶厂前瞻性队列23年的随访资料(1973~1995),研究的变量包括生活习惯、家庭环境、经济状况、职业因素、及个人人口学特征等,职业因素为5种橡胶化合物的暴露。根据以前分别分析的结果〔10〕,将研究疾病归为3种疾病类型,即肺癌、肠癌和胰腺癌、及缺血性心脏病和脑血管病。旨在研究①5种橡胶化合物的不同类型疾病危险度之间有无统计学差异;②恶性肿瘤与心脑血管疾病死因间的相互关系;③恶性肿瘤与心脑血管疾病间是否存在竞争性死亡等问题。
结果与分析
1.三种疾病类型间相互关系的描述
按死因类型分层,拟合Cox比例危险度的简单模型(没有包括其他协变量)。图1显示三种死因类型的生存曲线,表明55岁以前,三种疾病的死亡危险度均是很小的,曲线间互相交叉和重叠。50岁以后,生存率开始下降,以心、脑血管疾病最为明显。类型别死亡危险度是否随生存时期呈平滑的趋势(即按比例升高或下降),是通过将类型层变量拟造为时间协变量来检验的。如果包括所有年龄,比例危险度的假设检验统计量P值为临界水平(似然比=3.76,自由度为1,P=0.052)。如果排除小于50岁的生存年龄,显示约2%死因别危险度随生存年龄稍有上升,但比例危险度假设成立(似然比=1.95,自由度为1,P=0.163)。

, http://www.100md.com
图1 三种死因别生存率曲线
将死因类型变量指定为因子水平,进行简单模型的拟合,可以估计2个参数。肠癌和胰腺癌相对于肺癌的死亡危险度约40%,而心脑血管疾病死亡危险度约为肺癌的3倍,并均有统计意义。
2.慢性疾病史对三类死因的危险度
表2显示,在随访开始时记录有高血压疾病史的个体中,二类恶性肿瘤死亡危险度下降,心脑血管疾病死亡危险度增高,死因别危险度间的差别显著,既往心脏病史对死因别危险度没有明显的效应。慢性支气管炎在此作为参比,在死因别之间的危险度没有显著性差别。
表2 随访开始时疾病史的死因别危险度分析 疾病史
肺癌
肠癌和胰腺癌
, 百拇医药
心脑血管疾病
一致性检验
β
RR
β
RR
β
RR
似然比*
P值
高血压
-0.28
0.75
, http://www.100md.com
-0.26
0.77
0.78
2.20**
7.07
0.03
心脏病
0.16
1.18
-0.78
0.46
0.70
2.00**
, http://www.100md.com
3.91
0.14
慢性支气管炎
-0.06
0.94
0.84
2.31
-0.45
0.64
5.65
0.06
*自由度为2的似然比检验,**95%可信限不包括1。 3.职业暴露的死因别回归系数
, 百拇医药
将性别、疾病类型、吸烟、经济状态、血压、胆固醇等变量作为分层因素,拟合职业暴露主效应模型,并指定该模型为零模型。然后,将职业暴露变量与疾病类型因子的交互作用项引入模型,拟合并进行死因别回归系数的一致性检验。职业暴露为5种橡胶化合物,为指示变量形式。拟合结果见表3。亚硝胺暴露在三种死因类型间的危险度差别有统计意义。其中,亚硝胺暴露对于2种恶性肿瘤类型有明显的正性效应,相对危险度分别为2.25和2.92,肺癌危险度增高有统计意义。对于心血管疾病,亚硝胺暴露相对危险为1.02。其他4种橡胶化合物暴露的死因别危险度之间没有显著性差别。
表3 5种橡胶化合物死因别回归系数(生存年龄≥50岁) 职业暴露
肺 癌
肠癌和胰腺癌
心血管疾病
一致性检验
, 百拇医药
β
SE
RR
β
SE
RR
β
SE
RR
似然比*
P值
亚硝胺
0.81
, 百拇医药
0.32
2.25**
1.07
0.56
2.92
0.02
0.19
1.02
6.71
0.04
芳香胺
0.56
0.34
, 百拇医药
1.75
0.41
0.52
1.51
-0.07
0.18
0.93
3.22
0.20
溶剂
-0.42
0.42
0.66
, http://www.100md.com
0.18
0.52
1.20
0.03
0.19
1.03
1.15
0.56
滑石
0.02
0.33
1.02
-0.26
, http://www.100md.com
0.54
0.77
0.05
0.20
1.05
0.30
0.86
碳黑
0.24
0.31
1.26
0.74
0.51
, 百拇医药
2.10
-0.08
0.18
0.92
2.82
0.24
*自由度为2的似然比检验,**95%可信限不包括1。讨 论
对不同死因进行联合分析的方法并不需要死因间竞争性危险度相互独立的假设〔4,5〕,见式2,模型的似然函数为疾病类型项之乘积〔3〕。相对死因分别分析而言,联合分析的优点在于:
(1)可以估计疾病类型别危险度的差别,即进行疾病类型间相互关系的研究;
, 百拇医药
(2)在模型中估计各变量死因别的回归效应,分析那些效应是疾病类型共有的,那些是特定类型的;
(3)可以对疾病类型别的危险度差别进行正式的显著性检验,从而证明在分别分析中的结果;
(4)在联合分析模型中,不同疾病类型的死亡数合计大于分别分析中的死亡数,可使统计效率增高。
应用联合模型对5种橡胶化合物的死因别回归系数进行检验,只有亚硝胺暴露的危险度在三个死因类型间有显著性差别。其中,肺癌危险度显著增高。
三种疾病类型中,死亡危险度从高至低依次为心脑血管疾病、肺癌、以及肠和胰腺癌。心脑血管疾病死亡危险度显著地高于其他两类恶性肿瘤。由此考虑了心脑血管疾病与两类恶性肿瘤之间的相互关系。在此,不是认为心、脑血管疾病有预防恶性肿瘤的作用,而是认为它作为一种致死性疾病,与恶性肿瘤产生了竞争性死亡。于是,将既往患有高血压病史和心脏病史作为指示变量,应用比例危险度模型,估计死因别危险度。结果正如所预料的,在对多种混杂因子进行调整后,既往病史特别是高血压疾病史的心脑血管疾病死亡危险度增加,而其他两类恶性肿瘤死亡危险度下降,之间差别有统计学显著性。如果去除心脑血管疾病死因,剩下的两种恶性肿瘤的死亡危险度可能会发生很大变化。这是竞争性危险度分析中的焦点问题〔6〕。然而,已经证明,去死因的失效概率从(T,J,x)类型的资料中不能估计,这不是统计学的问题,而是生物学问题〔6〕。在生物学上,可考虑仅有一种方法移去心脑血管疾病死因,即假定有某种治疗药物能够控制和预防心脑血管疾病的死亡,延长其生命。这样在其他回归变量(x)效应不变情况下,恶性肿瘤的死亡概率可能会发生变化,应该增加。另一方面,概率可能又会受到该药物潜在的对两类恶性肿瘤效应的影响。
, http://www.100md.com
参考文献
1.Breslow NE,Day NE.Statistical methods in cancer research.VolⅡ.The design and analysis of cohort studies.Lyon:IARC,1987.
2.Chiang C L.Competing risks in mortality analysis.Annu Rev Health 1991,12:281.
3.Kalbfleish J D,Prentice R L.The statistical analysis of failure time data.New York:Wiley,1980,321.
4.Pierce D A,Preston D L Joint analysis of site-specific cancer risks for the Atomic Bomb Survivors.Radia Res,1993,134:134.
, 百拇医药
5.Lunn M,McNeil D.Applying Cox regression to competing risks.Biometrics.1995,51:524.
6.Prentice RL,Breslow NE.Retrospective studies and failure time models.Biometrika.1978,65:153.
7.Holt J D.Competing risk analysis with special reference to matched pair experiments.Biometrica.1978,65:159.
8.Aalen O.Nonparametric inference in connection with multiple decrement models.Scand J Stat,1976,3:15.
, 百拇医药
9.Larson MG.Covariate analysis of competing-risks data with Log linear models.Biometrics,1984,40:459.
中国微生态学杂志 1999年第1期第11卷 论著
饲喂乳杆菌对雏鸡盲肠8种正常菌群定植的影响
作者:刘永杰 赵艳兵 何梦辉 何昭阳
单位:刘永杰 赵艳兵 何梦辉 何昭阳 吉林农业大学动科系 长春 130118
关键词:乳杆菌;盲肠;正常菌群, 百拇医药