时间序列资料GM(0，N)预测模型及其应用
作者：许汝福 王文昌 易东 张蔚 尹全焕
单位：第三军医大学卫生统计学教研室(630038)
关键词：
中国卫生统计990313 多因素资料预测，一般使用最小二乘估计(LS估计)。但对于时间序列资料，LS估计未考虑各因素的发展变化的情况。本文介绍一种时间序列资料灰色GM(0，N)预测模型，通过实例应用，效果较为满意。
一、GM(0，N)模型建模方法
设x1={x1(1)，x1(2)，…，x1(n)}为应变量，xi={xi(1)，xi(2)，…，xi(n)}，i=2,3,…，N为自变量，xi，i=1,2,…，N均为时间序列资料，GM(0，N)模型建模步骤为：
, http://www.100md.com
1.初始化数据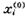
(k)=xi(k)/xi(1)
(1)
式中i=1,2,…，N；k=1,2,…，n，下同。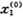
为应变量序列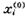，，i=2,3,…，N为自变量序列。
2.求GM(0，N)预测模型
令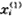
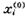为的1-AGO序列，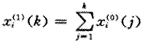
, http://www.100md.com
(2)
则GM(0，N)预测模型〔1〕为：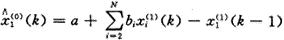
(3)
式中参数列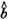
为：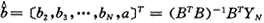
(4)
(5)
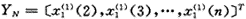
, http://www.100md.com (6)
二、应用
表1资料来源于我校第二附属医院病案统计室，收集了1985～1996年该院的年收治病人数(x1)，门急诊病人数(x2)、年平均开放病床数(x3)、实际占用床位总日数(x4)、病床使用率(x5)、出院者平均住院日数(x6)、病床周转次数(x7)。以1985～1995年的数据建立模型，对1996年该院年收治病人数进行预测。
表1 某院1985～1996年收治病人数及有关指标 年 份
年收治
病人数(x1)
, http://www.100md.com 门急诊人次
数(x2)
年均开放病
床数(x3)
实际占用床位
总日数(x4)
病床使用率
(x5)
平均住院日数
(x6)
病床周转次数
, 百拇医药
(x7)
1985
11671
473424
613.8
224042
102.30
19.2
19.01
1986
11942
497698
, 百拇医药 616.3
224962
102.71
18.8
18.71
1987
10923
495632
612.3
223502
102.06
20.5
17.84
, 百拇医药
1988
10601
393917
710.9
260205
92.69
24.5
14.91
1989
10158
334555
712.6
260092
, http://www.100md.com
92.09
25.6
14.26
1990
9541
365547
681.8
248838
87.07
26.1
13.99
1991
8957
, 百拇医药
411201
618.4
225707
95.14
25.2
14.48
1992
8673
342052
589.1
215040
90.64
24.8
, 百拇医药
14.72
1993
8519
304740
512.9
187204
78.91
22.0
16.61
1994
9100
302116
560.8
, http://www.100md.com
204676
86.27
22.5
16.23
1995
9644
288631
576.6
210476
99.94
21.9
16.68
1996
, 百拇医药
10522
232778
588.6
215434
102.01
20.6
17.74
1.模型建立
将原始数据初始化，按照上述方法计算得1986～1995年的GM(0，N)预测模型：
(k)=0.04219908+0.02022774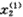
(k)+5.13585949
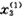(k)+5.91481912
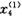(k)+0.05186225
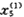(k)-0.33680961
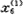(k)+0.47415729
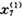(k)-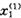
(k-1)。
, http://www.100md.com
式中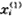(k)为初始化序列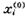(k)的1-AGO序列，见表2。表2 初始化序列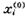的1-AGO序列 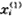年份
k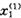
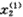
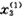
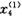
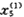
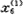
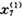
, http://www.100md.com
1985
1
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1986
2
2.023
2.051
, 百拇医药
2.004
2.004
2.004
1.979
1.984
1987
3
2.959
3.098
3.002
3.002
3.002
3.047
, 百拇医药
2.923
1988
4
3.867
3.930
4.160
4.163
3.908
4.380
3.707
1989
5
4.738
, http://www.100md.com
4.637
5.321
5.324
4.808
5.714
4.457
1990
6
5.555
5.409
6.432
6.435
5.659
, 百拇医药
7.073
5.193
1991
7
6.323
6.782
7.439
7.442
6.589
8.385
5.955
1992
8
, 百拇医药
7.066
7.000
8.399
8.402
7.475
9.677
6.730
1993
9
7.796
7.644
9.234
9.238
, http://www.100md.com
8.246
10.823
7.603
1994
10
8.576
8.282
10.148
10.151
9.090
11.995
8.457
1995
, 百拇医药
11
9.402
8.892
11.087
11.091
10.067
13.135
9.335
1996
12
10.303
9.383
12.046
, http://www.100md.com
12.052
11.064
14.208
10.268
应用LS估计计算得1985～1995年的回归方程：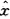
1=10950.8979+0.0010x2-177.0988x3+0.5291x4+2.1066x5-472.0405x6-42.6351x7
2.预测
1986～1996年医院年收治病人数的预测值见表3。GM(0，N)模型预测的最大相对误差为0.295%，LS估计的最大相对误差为1.35%，GM(0，N)模型的预测效果较优。1996年的实际值为10 522人次，GM(0，N)模型的预测值为10 553人次，LS估计的预测值为10 664人次，说明GM(0，N)模型的预测效果比较满意。
, 百拇医药
表3 某院1986～1996年收治病人数实际值及预测结果 年份
实际值
预测值
误 差
相对误差(%)
GM
LS
GM
LS
GM
LS
1986
11942
, http://www.100md.com
11941
11884
1
59
0.008
0.494
1987
10923
10918
11051
5
-128
0.046
, 百拇医药
-1.172
1988
10601
10590
10602
11
-1
0.104
-0.009
1989
10158
10162
10206
, 百拇医药
-4
-48
-0.039
-0.473
1990
9541
9521
9503
20
38
0.210
0.398
1991
, 百拇医药
8957
8962
8960
-5
-3
-0.056
-0.033
1992
8673
8649
8604
24
69
, 百拇医药
0.277
0.796
1993
8519
8520
8550
-1
-31
-0.012
-0.364
1994
9100
9080
, 百拇医药
9104
20
-4
0.220
-0.044
1995
9644
9631
9653
13
-9
0.135
-0.093
, 百拇医药
1996
10522
10553
10664
-31
-142
-0.295
-1.350
三、讨论 LS估计用原始数据进行计算，而GM(0，N)模型用初始化序列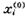(k)的1-AGO序列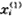(k)进行计算，由于AGO序列(累加生成序列)能弱化随机干扰〔1〕，比原始序列更能体现事物发展的规律。因此，GM(0，N)模型能较好地考虑各时间序列资料的发展变化情况，其预测效果比较满意。
参考文献
1.邓聚龙.灰色系统理论教程.武汉.华中理工大学出版社.1990., 百拇医药
单位：第三军医大学卫生统计学教研室(630038)
关键词：
中国卫生统计990313 多因素资料预测，一般使用最小二乘估计(LS估计)。但对于时间序列资料，LS估计未考虑各因素的发展变化的情况。本文介绍一种时间序列资料灰色GM(0，N)预测模型，通过实例应用，效果较为满意。
一、GM(0，N)模型建模方法
设x1={x1(1)，x1(2)，…，x1(n)}为应变量，xi={xi(1)，xi(2)，…，xi(n)}，i=2,3,…，N为自变量，xi，i=1,2,…，N均为时间序列资料，GM(0，N)模型建模步骤为：
, http://www.100md.com
1.初始化数据
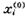(k)=xi(k)/xi(1)(1)
式中i=1,2,…，N；k=1,2,…，n，下同。
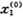为应变量序列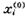，，i=2,3,…，N为自变量序列。2.求GM(0，N)预测模型
令
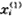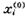为的1-AGO序列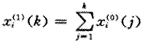，, http://www.100md.com
(2)
则GM(0，N)预测模型〔1〕为：
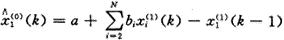
(3)
式中参数列
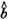为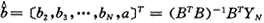：(4)
(5)
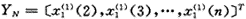
, http://www.100md.com (6)
二、应用
表1资料来源于我校第二附属医院病案统计室，收集了1985～1996年该院的年收治病人数(x1)，门急诊病人数(x2)、年平均开放病床数(x3)、实际占用床位总日数(x4)、病床使用率(x5)、出院者平均住院日数(x6)、病床周转次数(x7)。以1985～1995年的数据建立模型，对1996年该院年收治病人数进行预测。
表1 某院1985～1996年收治病人数及有关指标 年 份
年收治
病人数(x1)
, http://www.100md.com 门急诊人次
数(x2)
年均开放病
床数(x3)
实际占用床位
总日数(x4)
病床使用率
(x5)
平均住院日数
(x6)
病床周转次数
, 百拇医药
(x7)
1985
11671
473424
613.8
224042
102.30
19.2
19.01
1986
11942
497698
, 百拇医药 616.3
224962
102.71
18.8
18.71
1987
10923
495632
612.3
223502
102.06
20.5
17.84
, 百拇医药
1988
10601
393917
710.9
260205
92.69
24.5
14.91
1989
10158
334555
712.6
260092
, http://www.100md.com
92.09
25.6
14.26
1990
9541
365547
681.8
248838
87.07
26.1
13.99
1991
8957
, 百拇医药
411201
618.4
225707
95.14
25.2
14.48
1992
8673
342052
589.1
215040
90.64
24.8
, 百拇医药
14.72
1993
8519
304740
512.9
187204
78.91
22.0
16.61
1994
9100
302116
560.8
, http://www.100md.com
204676
86.27
22.5
16.23
1995
9644
288631
576.6
210476
99.94
21.9
16.68
1996
, 百拇医药
10522
232778
588.6
215434
102.01
20.6
17.74
1.模型建立
将原始数据初始化，按照上述方法计算得1986～1995年的GM(0，N)预测模型：
(k)=0.04219908+0.02022774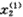(k)+5.13585949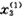(k)+5.91481912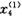(k)+0.05186225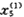(k)-0.33680961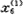(k)+0.47415729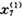(k)-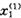(k-1)。, http://www.100md.com
式中
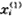(k)为初始化序列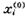(k)的1-AGO序列，见表2。表2 初始化序列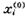的1-AGO序列 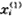年份k
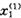
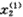
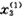
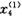
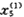
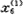
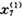
, http://www.100md.com
1985
1
1.000
1.000
1.000
1.000
1.000
1.000
1.000
1986
2
2.023
2.051
, 百拇医药
2.004
2.004
2.004
1.979
1.984
1987
3
2.959
3.098
3.002
3.002
3.002
3.047
, 百拇医药
2.923
1988
4
3.867
3.930
4.160
4.163
3.908
4.380
3.707
1989
5
4.738
, http://www.100md.com
4.637
5.321
5.324
4.808
5.714
4.457
1990
6
5.555
5.409
6.432
6.435
5.659
, 百拇医药
7.073
5.193
1991
7
6.323
6.782
7.439
7.442
6.589
8.385
5.955
1992
8
, 百拇医药
7.066
7.000
8.399
8.402
7.475
9.677
6.730
1993
9
7.796
7.644
9.234
9.238
, http://www.100md.com
8.246
10.823
7.603
1994
10
8.576
8.282
10.148
10.151
9.090
11.995
8.457
1995
, 百拇医药
11
9.402
8.892
11.087
11.091
10.067
13.135
9.335
1996
12
10.303
9.383
12.046
, http://www.100md.com
12.052
11.064
14.208
10.268
应用LS估计计算得1985～1995年的回归方程：
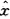1=10950.8979+0.0010x2-177.0988x3+0.5291x4+2.1066x5-472.0405x6-42.6351x72.预测
1986～1996年医院年收治病人数的预测值见表3。GM(0，N)模型预测的最大相对误差为0.295%，LS估计的最大相对误差为1.35%，GM(0，N)模型的预测效果较优。1996年的实际值为10 522人次，GM(0，N)模型的预测值为10 553人次，LS估计的预测值为10 664人次，说明GM(0，N)模型的预测效果比较满意。
, 百拇医药
表3 某院1986～1996年收治病人数实际值及预测结果 年份
实际值
预测值
误 差
相对误差(%)
GM
LS
GM
LS
GM
LS
1986
11942
, http://www.100md.com
11941
11884
1
59
0.008
0.494
1987
10923
10918
11051
5
-128
0.046
, 百拇医药
-1.172
1988
10601
10590
10602
11
-1
0.104
-0.009
1989
10158
10162
10206
, 百拇医药
-4
-48
-0.039
-0.473
1990
9541
9521
9503
20
38
0.210
0.398
1991
, 百拇医药
8957
8962
8960
-5
-3
-0.056
-0.033
1992
8673
8649
8604
24
69
, 百拇医药
0.277
0.796
1993
8519
8520
8550
-1
-31
-0.012
-0.364
1994
9100
9080
, 百拇医药
9104
20
-4
0.220
-0.044
1995
9644
9631
9653
13
-9
0.135
-0.093
, 百拇医药
1996
10522
10553
10664
-31
-142
-0.295
-1.350
三、讨论 LS估计用原始数据进行计算，而GM(0，N)模型用初始化序列
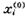(k)的1-AGO序列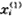(k)进行计算，由于AGO序列(累加生成序列)能弱化随机干扰〔1〕，比原始序列更能体现事物发展的规律。因此，GM(0，N)模型能较好地考虑各时间序列资料的发展变化情况，其预测效果比较满意。参考文献
1.邓聚龙.灰色系统理论教程.武汉.华中理工大学出版社.1990., 百拇医药