应用灰色预测模型精度检验初探
作者：徐玮 徐沪军 续海燕
单位：山东省济南市政府门诊部 济南250001
关键词：
数理医药学杂志990242
80年代初邓聚龙教授创立了“灰色系统理论”，被誉为未来的理论基础，在许多方面得到了应用，又在应用中获得了发展，受到了国内外许多学者的重视。目前预测模型已有许多种，GM(1，1)是数列预测最常用的一种。现以应用GM(1，1)预测模型为例，探讨在医学及地方病学中应用的精度检验及适宜条件，以便可以更好地指导实际工作，避免数学模型误用。
现以山东省平度县(大田村)地甲病的调查数字(见表1)建立灰色理论预测模型GM(1，1)进行精度检验。
由表1中算得一次累加值为W(i),i=1,2,…n为28，33.7，35.8，37.12，37.59…
, http://www.100md.com
表1 平度(大田)地甲病患病率 年限
1983
1984
1985
1986
1987
1988
1989
患病率%
28
5.7
2.1
1.32
, http://www.100md.com
0.47
0.23
0.12
根据W(i)微分拟合模型建立GM(1，1)模型
(i)=(W(i)-(u)/(a))e-a(i-1)-(u)/(a)
本例中：
(i)=(28-38.895)e0.7801(i-1)+38.895
由模型算得数值，经累减得：(i)…分别为28，5.933，2.703，1.231，0.561，0.256，0.117(见表2)。表2 山东平度(大田)1983～1989年地甲病患病率实际值与模型值比较 年 限
, http://www.100md.com
1983
1984
1985
1986
1987
1988
1989
累加值W(i)
28
33.7
35.8
37.12
37.59
, http://www.100md.com
38.798
37.937
模型累加值(i)
28
33.93
36.636
37.87
38.431
38.687
38.804
原始数据E(i)
28
5.7
, 百拇医药
2.1
1.32
0.47
0.32
0.12
模型还原数(i)
-
5.933
2.703
1.231
0.561
0.256
0.177
, 百拇医药
参差值ε(i)
0
-0.233
-0.603
0.089
-0.09
-0.026
0.003
误差百分比E%
-
-6.041
0.28
0.0674
, 百拇医药
0.193
0.113
0.025
应用GM(1，1)预测模型，必须评价精度高低，这关系到模型是否可以使用的问题。现进行精度检验。
1 残差检验
评价精度高低最简单的方法是看模型值和原值之间的百分比。我们认为地方病学中一般百分比±5%即为满意，对±20%以内的，根据实际情况也可以使用。如果再大即要考虑修正模型或改为其它模型。实际上如果原始数据摆动小，精度要比±5%小得多。
表3 预测模型精度等级评判
后验差比值C
误差概率P
, http://www.100md.com
1级(好)
<0.35
≥0.95
2级(合格)
<0.5
≥0.8
3级(勉强)
<0.65
≥0.7
4级(不合格)
≥0.65
<0.7
比较原始数据E(i)和还原数据(i)求出残值ε(i)和误差百分比E%。
, 百拇医药
ε(i)=E(i)-(i)见表2历年的残差值分别为-0.233,-0.603,0.089,-0.091……
E%=ε(i)/E(i)%见表2历年的误差百分比分别为0.041，0.28，0.0674，0.193…
预测1988年、1989年：本例与预测值相差为0.26，0.003，百分比为11.3%和2.5%。这样的数字我们根据实际情况可以接受，无须再用残差处理修正模型。
如果误差百分比过大，已不能使用，必须设法提高模型精度。一般提高精度方法即用残差数列建立类似的模型，以修正GM(1，1)(即两模型相加)，精度可以提高。如果仍达不到要求，可再进行残差处理，以求得满意的精度。
2 后验差检验
后验差检验可定为四个精度等级，见表3。
, http://www.100md.com
2.1 求残差均值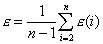
本例为-0.2095
2.2 求残差的方差
本例为0.3368
2.3 求原始数值均值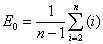
本例为-2.3975
2.4 求原始数值方差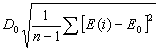
本例为1.9919
2.5 求后验差比
C=D/D 本例为0.1690,∵ <0.35 ∴ 精度为1级。
, 百拇医药
2.6 求小误差概率
P=P{|ε(i)-ε|<0.674D20} 本例1988年为0.1835，1998年为0.2525，<0.9062，所以此模型合格。
3 关联度检验
是根据模型曲线与数据曲线几何相似程度进行检验，是一种几何检验(也可以根据曲线间相似程度评判关联度。
精度检验往往是几种方法相结合，得出的结果大致相符。
4 讨论
4.1 通过预测模型，我们可以用以往数据预测以后，也可以在运用模型精度检验对用以往数字进行验证，进行分析是否合乎规律，通过精度的检验可得知模型的准确度、可靠性及适宜条件。进行精度检验，是确定模型能否使用的关键。
, 百拇医药
4.2 用灰色理论建模，一般采用三种精度检验方法：残差检验是模型精度按点检验，是一种直观的算述检验；后验差检验是按残差的概率分布进行的检验，是统计学检验；关联度检验是根据模型曲线与数据曲线的几何相似程度进行的检验，是几何检验。本文讨论了前两种方法。在实际应用中往往是几种相结合的检验。
4.3 在地方病学中，有些数据摆动性大，应用GM(1，1)建模评价精度不一定合格，有时相对误差很大，这就要设法提高精度，甚至多次残差处理，也可以换用其它模型。例如GM(1，2)即考虑了摆动情况。
4.4 目前灰色预测已在数学界应用。国内医学杂志多次报道了应用GM(1，1)模型的实例。有的用于车祸死亡人数预测及慢性病预测，相对误差高达48%，也未作精度检验，拟合效果也不好，这说明GM(1，1)预测并不适用于所有情况。它不是万能预测，而是有条件的预测。一般说来由于事物的发展惯性，可以进行短期预测，尤其内外环境变化不大的情况下。例如地方病学中患病率短期预测还是比较成功的，但长期预测就不一定适用，因未来的情况与目前的估计不一定相符，对长期规划和预测的估计尚有局限性。
, http://www.100md.com
参考文献
1 邓聚龙.灰色预测与决策.武汉：华中理工大学出版社，1988：59～135.
2 赵定义.灰色数例预测模型在医学中应用.中国卫生统计，1988，5(1)：5～7.
3 王乃平.灰色数例预测模型在防痨工作中应用.中国卫生统计，1990，7(3)：56.
4 王峰.应用数学模型评价疟防措施的效果.数理医药学杂志，1990，3(2)：45.
5 温志明.应用灰色动态模型预测疟疾发病与经济投入关系探讨.数理医药学杂志，1992，5(2)：76～78.
6 朱卉.武汉市车祸死亡人数灰色预测模型及其近期效果评价.中国卫生统计，1991，8(1)：58.
收稿日期：1998-11-03, http://www.100md.com
单位：山东省济南市政府门诊部 济南250001
关键词：
数理医药学杂志990242
80年代初邓聚龙教授创立了“灰色系统理论”，被誉为未来的理论基础，在许多方面得到了应用，又在应用中获得了发展，受到了国内外许多学者的重视。目前预测模型已有许多种，GM(1，1)是数列预测最常用的一种。现以应用GM(1，1)预测模型为例，探讨在医学及地方病学中应用的精度检验及适宜条件，以便可以更好地指导实际工作，避免数学模型误用。
现以山东省平度县(大田村)地甲病的调查数字(见表1)建立灰色理论预测模型GM(1，1)进行精度检验。
由表1中算得一次累加值为W(i),i=1,2,…n为28，33.7，35.8，37.12，37.59…
, http://www.100md.com
表1 平度(大田)地甲病患病率 年限
1983
1984
1985
1986
1987
1988
1989
患病率%
28
5.7
2.1
1.32
, http://www.100md.com
0.47
0.23
0.12
根据W(i)微分拟合模型建立GM(1，1)模型
(i)=(W(i)-(u)/(a))e-a(i-1)-(u)/(a)
本例中：
(i)=(28-38.895)e0.7801(i-1)+38.895
由模型算得数值，经累减得：(i)…分别为28，5.933，2.703，1.231，0.561，0.256，0.117(见表2)。表2 山东平度(大田)1983～1989年地甲病患病率实际值与模型值比较 年 限
, http://www.100md.com
1983
1984
1985
1986
1987
1988
1989
累加值W(i)
28
33.7
35.8
37.12
37.59
, http://www.100md.com
38.798
37.937
模型累加值(i)
28
33.93
36.636
37.87
38.431
38.687
38.804
原始数据E(i)
28
5.7
, 百拇医药
2.1
1.32
0.47
0.32
0.12
模型还原数(i)
-
5.933
2.703
1.231
0.561
0.256
0.177
, 百拇医药
参差值ε(i)
0
-0.233
-0.603
0.089
-0.09
-0.026
0.003
误差百分比E%
-
-6.041
0.28
0.0674
, 百拇医药
0.193
0.113
0.025
应用GM(1，1)预测模型，必须评价精度高低，这关系到模型是否可以使用的问题。现进行精度检验。
1 残差检验
评价精度高低最简单的方法是看模型值和原值之间的百分比。我们认为地方病学中一般百分比±5%即为满意，对±20%以内的，根据实际情况也可以使用。如果再大即要考虑修正模型或改为其它模型。实际上如果原始数据摆动小，精度要比±5%小得多。
表3 预测模型精度等级评判
后验差比值C
误差概率P
, http://www.100md.com
1级(好)
<0.35
≥0.95
2级(合格)
<0.5
≥0.8
3级(勉强)
<0.65
≥0.7
4级(不合格)
≥0.65
<0.7
比较原始数据E(i)和还原数据(i)求出残值ε(i)和误差百分比E%。
, 百拇医药
ε(i)=E(i)-(i)见表2历年的残差值分别为-0.233,-0.603,0.089,-0.091……
E%=ε(i)/E(i)%见表2历年的误差百分比分别为0.041，0.28，0.0674，0.193…
预测1988年、1989年：本例与预测值相差为0.26，0.003，百分比为11.3%和2.5%。这样的数字我们根据实际情况可以接受，无须再用残差处理修正模型。
如果误差百分比过大，已不能使用，必须设法提高模型精度。一般提高精度方法即用残差数列建立类似的模型，以修正GM(1，1)(即两模型相加)，精度可以提高。如果仍达不到要求，可再进行残差处理，以求得满意的精度。
2 后验差检验
后验差检验可定为四个精度等级，见表3。
, http://www.100md.com
2.1 求残差均值
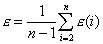本例为-0.20952.2 求残差的方差
本例为0.33682.3 求原始数值均值
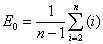本例为-2.39752.4 求原始数值方差
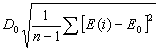本例为1.99192.5 求后验差比
C=D/D 本例为0.1690,∵ <0.35 ∴ 精度为1级。
, 百拇医药
2.6 求小误差概率
P=P{|ε(i)-ε|<0.674D20} 本例1988年为0.1835，1998年为0.2525，<0.9062，所以此模型合格。
3 关联度检验
是根据模型曲线与数据曲线几何相似程度进行检验，是一种几何检验(也可以根据曲线间相似程度评判关联度。
精度检验往往是几种方法相结合，得出的结果大致相符。
4 讨论
4.1 通过预测模型，我们可以用以往数据预测以后，也可以在运用模型精度检验对用以往数字进行验证，进行分析是否合乎规律，通过精度的检验可得知模型的准确度、可靠性及适宜条件。进行精度检验，是确定模型能否使用的关键。
, 百拇医药
4.2 用灰色理论建模，一般采用三种精度检验方法：残差检验是模型精度按点检验，是一种直观的算述检验；后验差检验是按残差的概率分布进行的检验，是统计学检验；关联度检验是根据模型曲线与数据曲线的几何相似程度进行的检验，是几何检验。本文讨论了前两种方法。在实际应用中往往是几种相结合的检验。
4.3 在地方病学中，有些数据摆动性大，应用GM(1，1)建模评价精度不一定合格，有时相对误差很大，这就要设法提高精度，甚至多次残差处理，也可以换用其它模型。例如GM(1，2)即考虑了摆动情况。
4.4 目前灰色预测已在数学界应用。国内医学杂志多次报道了应用GM(1，1)模型的实例。有的用于车祸死亡人数预测及慢性病预测，相对误差高达48%，也未作精度检验，拟合效果也不好，这说明GM(1，1)预测并不适用于所有情况。它不是万能预测，而是有条件的预测。一般说来由于事物的发展惯性，可以进行短期预测，尤其内外环境变化不大的情况下。例如地方病学中患病率短期预测还是比较成功的，但长期预测就不一定适用，因未来的情况与目前的估计不一定相符，对长期规划和预测的估计尚有局限性。
, http://www.100md.com
参考文献
1 邓聚龙.灰色预测与决策.武汉：华中理工大学出版社，1988：59～135.
2 赵定义.灰色数例预测模型在医学中应用.中国卫生统计，1988，5(1)：5～7.
3 王乃平.灰色数例预测模型在防痨工作中应用.中国卫生统计，1990，7(3)：56.
4 王峰.应用数学模型评价疟防措施的效果.数理医药学杂志，1990，3(2)：45.
5 温志明.应用灰色动态模型预测疟疾发病与经济投入关系探讨.数理医药学杂志，1992，5(2)：76～78.
6 朱卉.武汉市车祸死亡人数灰色预测模型及其近期效果评价.中国卫生统计，1991，8(1)：58.
收稿日期：1998-11-03, http://www.100md.com