灰色GM(1,1)模型在卫生资源预测中的应用
作者:严云良
单位:浙江中医学院 杭州310009
关键词:GM(1,1)模型;预测;卫生资源;医生数;床位数
数理医药学杂志990238
摘要 应用灰色GM(1,1)模型对浙江省1988~1997年的病床数和医生数进行拟合,得病床数拟合模型为(t+1)=619.7693e0.015438t-610.59972,拟合精度99%;得医生数拟合模型为(t+1)=204.5117e0.027837t-198.879,拟合精度为98.53%。预测了1999~2005年浙江省应配置的医生数和床位数。
我们在研究浙江省卫生资源配置标准时,需对1999~2005年的卫生资源的配置进行预测。传统的直线回归法和指数法预测误差较大,为提高预测精度,我们采用GM(1,1)模型进行预测,预测效果良好。
, 百拇医药
1 资料来源
预测样本来自1988~1997年浙江省统计年鉴,历年的医生数和床位数见表1。
表1 浙江省1988~1997年医生数、床位数统计表 年份
1988
1989
1990
1991
1992
1993
1994
1995
, 百拇医药 1996
1997
医生数(人)
56327
58087
59072
60252
60982
61361
63730
66838
69167
72242
, 百拇医药
病床数(张)
91721
95262
97114
99282
101721
104033
105999
106421
106246
107732
2 方法
2.1 一次累加生成数据
, http://www.100md.com
设原始数据资料为X(0),X(1),…,X(n),对X作一次累加生成数据得: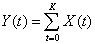 , k=0,1,…,n (1)
, k=0,1,…,n (1)
2.2 均值生成数据
对累加生成数据Y(t)按
Z(t)=1/2[Y(t)+Y(t-1)] t=1,2,…,n (2)
2.3 建立Y(t)的一阶微分方程 ,其中a和U满足微分方程
,其中a和U满足微分方程 (3)
(3)
由矩阵运算得 (4)
(4)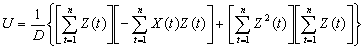 (5)
(5) (6)
(6)
, 百拇医药
3 计算步骤与结果分析
3.1 建立预测模型
按公式(1)、(2),求出床位数累加生成数据Y(t)和均值生成数据Z(t),结果见表2。
表2 床位数累加生成数据和均值生成数据 年份
1988
1989
1990
1991
1992
1993
1994
, 百拇医药
1995
1996
1997
∑
t
0
1
2
3
4
5
6
7
8
, 百拇医药
9
X(t)
9.1721
9.5762
9.7114
9.9282
10.1721
10.4033
10.5999
10.6421
10.6246
10.7732
, 百拇医药 92.381
Y(t)
9.1721
18.6983
28.4097
38.3379
48.51
58.9133
69.5132
80.1553
90.7799
101.4045
, http://www.100md.com
Z(t)
13.9352
23.554
33.3738
43.42395
53.7117
64.2133
74.8343
85.4676
96.0922
488.6061
Z2(t)
, http://www.100md.com
194.1898
554.7909
1113.8105
1885.6394
2884.9413
4123.3415
5600.1650
7304.7107
9233.7109
32895.3193
Z(t)X(t)
132.7495
, 百拇医药
228.7423
331.3418
441.7128
558.7789
680.6546
796.3941
908.0591
1035.2705
5133.6536
将表2最后一列代入公式(6)、(4)、(5)得:
D=57321.9528 a=-0.015438
, http://www.100md.com
U=9.4264 U/a=610.5972
将a、U代入公式(3)即得GM(1,1)模型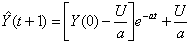
=619.7693e0.015438t-610.5972 (7)
按上述步骤建立医生数的预测模型得: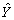 (t+1)=204.5117e0.027387t-198.8790 (8)
(t+1)=204.5117e0.027387t-198.8790 (8)
3.2 检验所建模型的预测结果
以病床数预测模型为例,按公式(7)计算1989~1997年的病床数累加数据估计值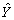 (t),再按公式
(t),再按公式 (t)=
(t)=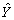 (t)-
(t)-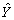 (t-1),t=1,2,…,n,计算1989~1997年病床数估计值
(t-1),t=1,2,…,n,计算1989~1997年病床数估计值 (t),结果见表3。
(t),结果见表3。
, http://www.100md.com
表3 实测值X(t)与预测值 (t)比较 年份
(t)比较 年份
1989
1990
1991
1992
1993
1994
1995
1996
1997
实测值X(t)
, http://www.100md.com
95262
97114
99282
101721
104033
105999
106421
106246
107732
预测值X(t)
96422
97923
, http://www.100md.com 99446
100993
102564
104160
105781
107426
109097
|X(t)-X(t)|
1160
809
164
728
1469
, 百拇医药
1839
640
1180
1365
相对误差%
1.218
0.833
0.165
0.716
1.412
1.735
0.601
1.111
, http://www.100md.com
1.267
从表3可以看出实测值和预测值大体上是接近的,平均相对误差1%,最大相对误差1.735%。说明这一预测模型是可信的。
按照医生数的预测模型,根据上述方法,计算医生数的估计值 (t),以检验医生预测模型,结果见表4。表4 实测值X(t)与预测值
(t),以检验医生预测模型,结果见表4。表4 实测值X(t)与预测值 (t)比较 年份
(t)比较 年份
1989
1990
1991
1992
1993
, 百拇医药
1994
1995
1996
1997
实测值X(t)
58087
59072
60252
60982
61361
63730
66838
69267
, http://www.100md.com
72242
预测值X(t)
56784
58360
59981
61646
63357
65117
66925
68783
70693
|X(t)-X(t)|
, 百拇医药 1303
712
271
664
1996
1387
87
384
1549
相对误差%
2.24
1.205
0.449
, http://www.100md.com
1.089
3.25
2.18
0.13
0.555
2.14
由表4可以看出,医生数的预测值 (t)与实际值X(t)相差不大,平均相对误差为1.47%,说明可接受所建的医生数预测模型。
(t)与实际值X(t)相差不大,平均相对误差为1.47%,说明可接受所建的医生数预测模型。
3.3 外推预测
根据所建的灰色GM(1,1)模型(7)和(8),分别预测浙江省1999~2005年的应配置的病床数和医生数,结果见表5。表5 1999~2005年医生数和床位数预测数 年份
, 百拇医药
1999
2000
2001
2002
2003
2004
2005
医生数(人)
74672
76748
78877
81067
83318
, 百拇医药
85632
88009
床位数(张)
112519
114269
116047
117852
119686
121548
123438
4 讨论
4.1 我们对卫生资源配置预测时,是建立在承认现实合理性的基础上的。事实上,目前我省有限的卫生资源的布局和结构不尽合理,卫生资源的短缺和浪费并存。因此区域卫生资源的配置应坚持调整存量、优化增量、提高质量的方针。通过新增资源的优先配置和存量资源调整,使卫生资源配置逐步趋于合理。
, 百拇医药
4.2 医生数和病床数是卫生资源配置中最重要的指标,本文仅对卫生资源配置中的床位数和医生数作了预测。卫生资源中的卫技人员、护理人员、防保人员、工勤人员等的配置数也可用灰色GM(1,1)模型预测,但一般可按比例法配置,故不再一一赘述。
4.3 灰色GM(1,1)模型受样本含量和概率分布的限制较小,运算简单,对近期预测有较高实用价值,是值得推广和应用的方法。
参考文献
1 邓聚龙.灰色系统理论的GM模型.模糊数学.1985,5(2):26.
2 姚水才,等.区域卫生规划指导使用手册.人民卫生出版社,1997,37~45.
3 赵定义.灰色数列预测模型在医学中的应用.中国卫生统计,1988,5(1):5.
4 鹿炳武.灰色数列预测模型在尘肺发病中的应用.中国卫生统计,1996,13(2):46.
5 娄培安.用灰色GM(1,1)模型对间日疟流行态势的研究.数理医药学杂志,1998,11(2):106.
收稿日期:1999-01-26, http://www.100md.com
单位:浙江中医学院 杭州310009
关键词:GM(1,1)模型;预测;卫生资源;医生数;床位数
数理医药学杂志990238
摘要 应用灰色GM(1,1)模型对浙江省1988~1997年的病床数和医生数进行拟合,得病床数拟合模型为(t+1)=619.7693e0.015438t-610.59972,拟合精度99%;得医生数拟合模型为(t+1)=204.5117e0.027837t-198.879,拟合精度为98.53%。预测了1999~2005年浙江省应配置的医生数和床位数。
我们在研究浙江省卫生资源配置标准时,需对1999~2005年的卫生资源的配置进行预测。传统的直线回归法和指数法预测误差较大,为提高预测精度,我们采用GM(1,1)模型进行预测,预测效果良好。
, 百拇医药
1 资料来源
预测样本来自1988~1997年浙江省统计年鉴,历年的医生数和床位数见表1。
表1 浙江省1988~1997年医生数、床位数统计表 年份
1988
1989
1990
1991
1992
1993
1994
1995
, 百拇医药 1996
1997
医生数(人)
56327
58087
59072
60252
60982
61361
63730
66838
69167
72242
, 百拇医药
病床数(张)
91721
95262
97114
99282
101721
104033
105999
106421
106246
107732
2 方法
2.1 一次累加生成数据
, http://www.100md.com
设原始数据资料为X(0),X(1),…,X(n),对X作一次累加生成数据得:
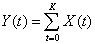 , k=0,1,…,n (1)
, k=0,1,…,n (1)2.2 均值生成数据
对累加生成数据Y(t)按
Z(t)=1/2[Y(t)+Y(t-1)] t=1,2,…,n (2)
2.3 建立Y(t)的一阶微分方程
 ,其中a和U满足微分方程
,其中a和U满足微分方程 (3)
(3)由矩阵运算得
 (4)
(4)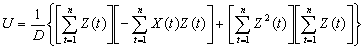 (5)
(5) (6)
(6), 百拇医药
3 计算步骤与结果分析
3.1 建立预测模型
按公式(1)、(2),求出床位数累加生成数据Y(t)和均值生成数据Z(t),结果见表2。
表2 床位数累加生成数据和均值生成数据 年份
1988
1989
1990
1991
1992
1993
1994
, 百拇医药
1995
1996
1997
∑
t
0
1
2
3
4
5
6
7
8
, 百拇医药
9
X(t)
9.1721
9.5762
9.7114
9.9282
10.1721
10.4033
10.5999
10.6421
10.6246
10.7732
, 百拇医药 92.381
Y(t)
9.1721
18.6983
28.4097
38.3379
48.51
58.9133
69.5132
80.1553
90.7799
101.4045
, http://www.100md.com
Z(t)
13.9352
23.554
33.3738
43.42395
53.7117
64.2133
74.8343
85.4676
96.0922
488.6061
Z2(t)
, http://www.100md.com
194.1898
554.7909
1113.8105
1885.6394
2884.9413
4123.3415
5600.1650
7304.7107
9233.7109
32895.3193
Z(t)X(t)
132.7495
, 百拇医药
228.7423
331.3418
441.7128
558.7789
680.6546
796.3941
908.0591
1035.2705
5133.6536
将表2最后一列代入公式(6)、(4)、(5)得:
D=57321.9528 a=-0.015438
, http://www.100md.com
U=9.4264 U/a=610.5972
将a、U代入公式(3)即得GM(1,1)模型
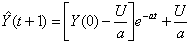
=619.7693e0.015438t-610.5972 (7)
按上述步骤建立医生数的预测模型得:
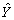 (t+1)=204.5117e0.027387t-198.8790 (8)
(t+1)=204.5117e0.027387t-198.8790 (8)3.2 检验所建模型的预测结果
以病床数预测模型为例,按公式(7)计算1989~1997年的病床数累加数据估计值
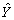 (t),再按公式
(t),再按公式 (t)=
(t)=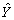 (t)-
(t)-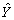 (t-1),t=1,2,…,n,计算1989~1997年病床数估计值
(t-1),t=1,2,…,n,计算1989~1997年病床数估计值 (t),结果见表3。
(t),结果见表3。, http://www.100md.com
表3 实测值X(t)与预测值
 (t)比较 年份
(t)比较 年份1989
1990
1991
1992
1993
1994
1995
1996
1997
实测值X(t)
, http://www.100md.com
95262
97114
99282
101721
104033
105999
106421
106246
107732
预测值X(t)
96422
97923
, http://www.100md.com 99446
100993
102564
104160
105781
107426
109097
|X(t)-X(t)|
1160
809
164
728
1469
, 百拇医药
1839
640
1180
1365
相对误差%
1.218
0.833
0.165
0.716
1.412
1.735
0.601
1.111
, http://www.100md.com
1.267
从表3可以看出实测值和预测值大体上是接近的,平均相对误差1%,最大相对误差1.735%。说明这一预测模型是可信的。
按照医生数的预测模型,根据上述方法,计算医生数的估计值
 (t),以检验医生预测模型,结果见表4。表4 实测值X(t)与预测值
(t),以检验医生预测模型,结果见表4。表4 实测值X(t)与预测值 (t)比较 年份
(t)比较 年份1989
1990
1991
1992
1993
, 百拇医药
1994
1995
1996
1997
实测值X(t)
58087
59072
60252
60982
61361
63730
66838
69267
, http://www.100md.com
72242
预测值X(t)
56784
58360
59981
61646
63357
65117
66925
68783
70693
|X(t)-X(t)|
, 百拇医药 1303
712
271
664
1996
1387
87
384
1549
相对误差%
2.24
1.205
0.449
, http://www.100md.com
1.089
3.25
2.18
0.13
0.555
2.14
由表4可以看出,医生数的预测值
 (t)与实际值X(t)相差不大,平均相对误差为1.47%,说明可接受所建的医生数预测模型。
(t)与实际值X(t)相差不大,平均相对误差为1.47%,说明可接受所建的医生数预测模型。3.3 外推预测
根据所建的灰色GM(1,1)模型(7)和(8),分别预测浙江省1999~2005年的应配置的病床数和医生数,结果见表5。表5 1999~2005年医生数和床位数预测数 年份
, 百拇医药
1999
2000
2001
2002
2003
2004
2005
医生数(人)
74672
76748
78877
81067
83318
, 百拇医药
85632
88009
床位数(张)
112519
114269
116047
117852
119686
121548
123438
4 讨论
4.1 我们对卫生资源配置预测时,是建立在承认现实合理性的基础上的。事实上,目前我省有限的卫生资源的布局和结构不尽合理,卫生资源的短缺和浪费并存。因此区域卫生资源的配置应坚持调整存量、优化增量、提高质量的方针。通过新增资源的优先配置和存量资源调整,使卫生资源配置逐步趋于合理。
, 百拇医药
4.2 医生数和病床数是卫生资源配置中最重要的指标,本文仅对卫生资源配置中的床位数和医生数作了预测。卫生资源中的卫技人员、护理人员、防保人员、工勤人员等的配置数也可用灰色GM(1,1)模型预测,但一般可按比例法配置,故不再一一赘述。
4.3 灰色GM(1,1)模型受样本含量和概率分布的限制较小,运算简单,对近期预测有较高实用价值,是值得推广和应用的方法。
参考文献
1 邓聚龙.灰色系统理论的GM模型.模糊数学.1985,5(2):26.
2 姚水才,等.区域卫生规划指导使用手册.人民卫生出版社,1997,37~45.
3 赵定义.灰色数列预测模型在医学中的应用.中国卫生统计,1988,5(1):5.
4 鹿炳武.灰色数列预测模型在尘肺发病中的应用.中国卫生统计,1996,13(2):46.
5 娄培安.用灰色GM(1,1)模型对间日疟流行态势的研究.数理医药学杂志,1998,11(2):106.
收稿日期:1999-01-26, http://www.100md.com