医院科室综合评价的数学模型
作者:张双德
单位:张双德(武警医学院数学教研室 天津300162)
关键词:综合评价;指标因素;权重
数理医药学杂志000107
摘 要:应用层次分析法建立了医院科室综合评价的数学模型,该模型具有较强的实际应用意义,并可作进一步的推广。
中图分类号:O 242
文章编号:1004-4337(2000)01-0015-03▲
1 问题的提出
在医院科室综合考评工作中,以往多采用定性分析、单因素考核的方法,在其过程中容易受到较多主观因素的影响,往往会出现偏离客观、公正的现象。如果利用数学方法将这些定性分析的考核指标进行量化,把多种考核因素作综合系统分析,就会避免许多因主观引起的弊端,所得结果将会更加科学与合理。
, http://www.100md.com
美国著名运筹学家T.L.Saaty教授于70年代初提出的层次分析法(Analytic Hierarch Process)就是一种简便、灵活的多准则决策的数学方法,它可以实现由定性到定量的转化,把复杂的问题系统化、层次化。为此,我们利用层次分析法来建立医院科室综合考核的数学模型。
2 建模与求解
2.1 确定评价指标体系
确定综合评价指标体系是进行评价工作的基础,由评价对象和评价目的的不同,所选的评价指标就有所不同,我们限定的被评价对象是医院的技术科室。通过查阅大量有关医院管理方面的资料和向有关专家及医院管理人员作调查,同时又考虑到实际操作的简单性、可行性原则,最后确定出用于综合评价的指标体系。该体系包括两级评价指标。第一级指标包括队伍结构(C1)、组织管理(C2)、业务能力(C3)三项内容。第二级指标包括10项内容,是由一级指标分解出的子指标,队伍结构分解为:年龄、学历、职称结构(C11)、业务与学术水平(C12)、人才培养和值班情况(C13);组织管理分解为:团结协作(C21)、制度健全(C22)、服务质量(C23)、完成任务情况(C24);业务能力分解为:疑难病症诊治能力(C31)、危重病人抢救能力(C32)、开拓创新能力(C33)。
, http://www.100md.com
为了清晰起见,我们把已得到的评价指标体系按照总目的、一级指标和二级指标划分为三个不同层次。第一层为综合评价层,第二层为一级评价指标层,第三层为二级指标层,最下层为待评价的对象。
下面的任务就是要确定各项指标因素的权重。为了更加全面地反映各指标对于综合评价的影响程度,我们采用层次分析法确定各指标的权重。
2.2 各指标相对重要性的比较
为了便于把各指标重要程度的定性描述转化为定量分析,我们把任意两因素对评价目标影响的强度划分为相同、较强、强、很强、绝对强五种程度。通过调查和征求有关方面的意见,得到各指标相对重要性的比较结果如下:
相对于综合评价总目标Z,队伍结果(C1)、组织管理(C2)、业务能力(C3)这三项指标两两比较的结果为:C1“较强”于C2,C3“强”于C1,C3“较强”于C2;
, http://www.100md.com
相对于队伍结构(C1)有:C11“相同”于C13,C12“强”于C11,C12“强”于C13;
相对于组织管理(C2)有:C21“稍稍强”于C22,C23“强”于C21,C24“强”于C21,C23“较强”于C22,C24“较强”于C22,C23“相同”于C24;
相对于业务能力(C3)有:C31“强”于C33,C32“较强”于C31,C32“稍稍强”于C33。
, 百拇医药
2.3 构造比较判断矩阵
为把上面各指标比较得到的经验结果转化为比较判断矩阵(aij)n×n,这里aij表示两指标重要程度的比,我们采取1~9尺度[1],确定aij的取值如下:
(1) 当xi与xj的影响程度“相同”时,取aij=1;
(2) 当xi与xj“较强”时,取aij=3;
(3) 当xi与xj“强”时,取aij=5;
(4) 当xi与xj“很强”时,取aij=7;
, 百拇医药
(5) 当xi与xj“绝对强”时,取aij=9;
(6) 当xi与xj的影响程度介于上述五种情况的相邻两者之间时,取aij为两个判断值的平均,即2、4、6、8之一;
(7) 当xi与xj的影响之比aji取aij的倒数。
于是,得到第一级指标(第二层C1~C3)关于评价总目标层Z的比较判断矩阵Z-C和第二级指标(第三层C11~C33)关于第一指标的比较判断矩阵C1~C1j,C2~C2j,C3~C3j分别是

, 百拇医药
2.4 确定权重向量
由比较判断矩阵确定各指标因素的权重有多种方法,这里我们取矩阵的最大特征值λmax所对应的归一化的特征向量ω=(ω1,ω2,…,ωn)作为诸指标的权重向量。
基于求矩阵特征值和特征向量的困难,下面我们利用“求和法”近似计算比较判断矩阵的最大特征值和特征向量,其步骤是:
(1) 将比较判断矩阵A的列向量归一化得, ij=
ij=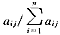 ;
;
(2) 对 ij按行求和得
ij按行求和得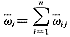 ;
;
, http://www.100md.com
(3) 将 i归一化
i归一化 ,即得近似特征向量ω=(ω1,ω2,…,ωn)T ;
,即得近似特征向量ω=(ω1,ω2,…,ωn)T ;
(4) 计算 ,作为最大特征值的近似值。其中(Aω)i是Aω的第i个分量。
,作为最大特征值的近似值。其中(Aω)i是Aω的第i个分量。
定义 作为衡量所得权重向量是否合理的指标,称CR为随机一致性比率,其中
作为衡量所得权重向量是否合理的指标,称CR为随机一致性比率,其中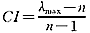 称为一致性指标,RI称为随机一致性指标(其具体数值由下表给出)。当
称为一致性指标,RI称为随机一致性指标(其具体数值由下表给出)。当 <0.1时,由上得到的归一化的特征向量即作为评价指标的权重向量。否则,说明比较判断矩阵不够合理,需要进行调整。这一步称为一致性检验。表1给出了用于判断的随机一致性指标RI的数值。
<0.1时,由上得到的归一化的特征向量即作为评价指标的权重向量。否则,说明比较判断矩阵不够合理,需要进行调整。这一步称为一致性检验。表1给出了用于判断的随机一致性指标RI的数值。
, 百拇医药
表1 随机一致性指标RI的值 n
1
2
3
4
5
6
7
8
9
10
11
RI
0
, http://www.100md.com
0
0.58
0.90
1.12
1.24
1.32
1.41
1.45
1.49
1.51
其中n为比较判断矩阵的阶数。
现在利用“求和法”计算上面各个比较判断矩阵的权向量(这里略去具体的计算过程)为:
, http://www.100md.com
矩阵Z~Ci的权向量和最大特征值是:
ωz=(0.1061,0.2605,0.6334)T, λzmax=3.0386
按照一致性检验公式,分别计算一致性指标CIz和一致性比率CRz得:
CIz=0.0193,RIz=0.85,CRz=0.03<0.1
由于CRz=0.03<0.1,可见比较矩阵Z~Ci具有满意的一致性,所以由此得到的权向量是可行的,即C1,C2,C3关于Z的权重分别是0.1061,0.2605,0.6334。这说明对于综合考评来讲,一级指标层中的3项指标相对重要的是业务能力,其次是组织管理,最后是队伍结构。
, 百拇医药
类似可以得到其它三个矩阵的权向量、最大特征值、一致性指标和一致性比率分别是:
ωC1=(0.2,0.6,0.2)T, λC1maxmax=3
CIC1=0,RIC1=0.58,CRC1=0<0.1;
ωC2=(0.1165,0.1044,0.3895,0.3895)T, λC2maxmax=4.1935
, http://www.100md.com CIC2=0.0645,RIC2=0.9,CRC21=0.0716<0.1;
ωC3=(0.2518,0.5889,0.1593)T, λC3maxmax=3.0539
CIC3=0.027,RIC3=0.58,CRC3=0.0465<0.1。
各矩阵都通过了一致性的检验,如此我们得到了各子指标对于第二层每个指标的权重。为了得到这10项指标因素(Cij)对于综合考评这一总目标的权重(即给出层次总排序),按下列方法进行计算:
, http://www.100md.com
设一级指标层中3项指标因素C1,C2,C3的权重是a1,a2,a3,二级指标层中10项指标因素D1,D2,…,D10的权重分别是d1j,d2j,…,d10j,(j=1,2,3),(当Di与Cj无联系时记dij=0)。那么Di关于总目标Z的权重就是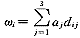 (i=1,2,…,10),于是,第二级指标层中10项指标因素的总排序即总的权向量是:
(i=1,2,…,10),于是,第二级指标层中10项指标因素的总排序即总的权向量是:
ω=(ω1,ω2,…,ω10)T
, 百拇医药
层次总排序也要进行一致性检验,设二经指标层中某些指标对Cj单排序的一致性指标为CIj,随机一致性指标为RIj,则二级指标层总排序的随机一致性比率定义为: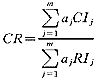
当CR<0.1时,认为层次总排序具有满意的程度。
现按此计算方法,求10项指标对于综合评价总目标的层次总排序,对于没有隶属影响的权值记为0,所得结果见表2。
表2 10项指标的权重总排序 第二层C
第三层D
C1
C2
, 百拇医药
C3
层次总
排序∑
0.1061
0.2605
0.6334
C11
0.2
0
0
0.0212
C12
, http://www.100md.com
0.6
0
0
0.0640
C13
0.2
0
0
0.0212
C21
0
0.1165
0
, 百拇医药
0.0303
C22
0
0.1044
0
0.0272
C23
0
0.3895
0
0.1015
C24
, 百拇医药
0
0.3895
0
0.1015
C31
0
0
0.2518
0.1599
C32
0
0
0.3730
, http://www.100md.com
0.3730
C33
0
0
0.1593
0.1009
进行总体一致性检验:
故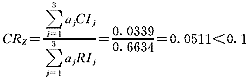
可见,得到的10项指标因素对于总评价目标的权向量是可接受的。于是,按照权重大小得到的10项指标因素相对于评价总目标重要程度的总排序是:
, 百拇医药
C32,C31,C23,C24,C33,C12,C13,C21,C11,C13
它们的权重分别由表2中右边一栏的数据给出。由上述过程可知,各项权重是对所有指标因素进行综合评判得到的,因此,具有较好的客观性和公正性。
由此可见,在10项考评指标中,相对重要的是第9项“对危重病人的抢救能力”、第8项“对疑难病症的诊治能力”、第6项“服务质量”、第7项“完成任务情况”、第10项“开拓创新能力”和第2项“业务与学术水平”。这里明显地体现了科室整体的专业能力、服务质量和完成任务情况。它们在综合评价中所占的权重分别是0.3730、0.1599、0.1015、0.1015、0.1009、0.064,占10项指标总权重的83.68%。
, http://www.100md.com
3 模型评述
3.1 对评价指标两两比较的结果,是由专家根据其客观经验确定的,可能会因不同的专家而异,可以请各专家分别给出比较结果,然后取其众数作为专家组一致的意见,但亦可采用其他方式,比如讨论协商等,达成一致的结果。
3.2 该模型给出了如何将评价的定性描述转化为定量分析的一般方法,并且算法也较为简单(通过简单的计算器即可完成),具有一般性,因此可以推广到许多类似的问题上去。
3.3 在实际使用中,各指标的权重只须取其两位有效数字即可。
3.4 对具体被评价的对象,应该就每一项指标按照五种比较强度标准建立相应的比较判断矩阵,计算各对象对每一指标的权重,最后计算各对象的层次总排序,但这不便于实际操作。因此,对每一项评价指标可以采取直接给评价对象打分,然后按上述权重计算加权平均,最后给出总排序就简单多了。■
参考文献:
[1] 王莲芬,许树柏.层次分析法引论.中国人民大学出版社,1990.
[2] 姜启源.数学模型(第二版).高等教育出版社,1997.
收稿日期:1999-03-22, 百拇医药
单位:张双德(武警医学院数学教研室 天津300162)
关键词:综合评价;指标因素;权重
数理医药学杂志000107
摘 要:应用层次分析法建立了医院科室综合评价的数学模型,该模型具有较强的实际应用意义,并可作进一步的推广。
中图分类号:O 242
文章编号:1004-4337(2000)01-0015-03▲
1 问题的提出
在医院科室综合考评工作中,以往多采用定性分析、单因素考核的方法,在其过程中容易受到较多主观因素的影响,往往会出现偏离客观、公正的现象。如果利用数学方法将这些定性分析的考核指标进行量化,把多种考核因素作综合系统分析,就会避免许多因主观引起的弊端,所得结果将会更加科学与合理。
, http://www.100md.com
美国著名运筹学家T.L.Saaty教授于70年代初提出的层次分析法(Analytic Hierarch Process)就是一种简便、灵活的多准则决策的数学方法,它可以实现由定性到定量的转化,把复杂的问题系统化、层次化。为此,我们利用层次分析法来建立医院科室综合考核的数学模型。
2 建模与求解
2.1 确定评价指标体系
确定综合评价指标体系是进行评价工作的基础,由评价对象和评价目的的不同,所选的评价指标就有所不同,我们限定的被评价对象是医院的技术科室。通过查阅大量有关医院管理方面的资料和向有关专家及医院管理人员作调查,同时又考虑到实际操作的简单性、可行性原则,最后确定出用于综合评价的指标体系。该体系包括两级评价指标。第一级指标包括队伍结构(C1)、组织管理(C2)、业务能力(C3)三项内容。第二级指标包括10项内容,是由一级指标分解出的子指标,队伍结构分解为:年龄、学历、职称结构(C11)、业务与学术水平(C12)、人才培养和值班情况(C13);组织管理分解为:团结协作(C21)、制度健全(C22)、服务质量(C23)、完成任务情况(C24);业务能力分解为:疑难病症诊治能力(C31)、危重病人抢救能力(C32)、开拓创新能力(C33)。
, http://www.100md.com
为了清晰起见,我们把已得到的评价指标体系按照总目的、一级指标和二级指标划分为三个不同层次。第一层为综合评价层,第二层为一级评价指标层,第三层为二级指标层,最下层为待评价的对象。
下面的任务就是要确定各项指标因素的权重。为了更加全面地反映各指标对于综合评价的影响程度,我们采用层次分析法确定各指标的权重。
2.2 各指标相对重要性的比较
为了便于把各指标重要程度的定性描述转化为定量分析,我们把任意两因素对评价目标影响的强度划分为相同、较强、强、很强、绝对强五种程度。通过调查和征求有关方面的意见,得到各指标相对重要性的比较结果如下:
相对于综合评价总目标Z,队伍结果(C1)、组织管理(C2)、业务能力(C3)这三项指标两两比较的结果为:C1“较强”于C2,C3“强”于C1,C3“较强”于C2;
, http://www.100md.com
相对于队伍结构(C1)有:C11“相同”于C13,C12“强”于C11,C12“强”于C13;
相对于组织管理(C2)有:C21“稍稍强”于C22,C23“强”于C21,C24“强”于C21,C23“较强”于C22,C24“较强”于C22,C23“相同”于C24;
相对于业务能力(C3)有:C31“强”于C33,C32“较强”于C31,C32“稍稍强”于C33。
, 百拇医药
2.3 构造比较判断矩阵
为把上面各指标比较得到的经验结果转化为比较判断矩阵(aij)n×n,这里aij表示两指标重要程度的比,我们采取1~9尺度[1],确定aij的取值如下:
(1) 当xi与xj的影响程度“相同”时,取aij=1;
(2) 当xi与xj“较强”时,取aij=3;
(3) 当xi与xj“强”时,取aij=5;
(4) 当xi与xj“很强”时,取aij=7;
, 百拇医药
(5) 当xi与xj“绝对强”时,取aij=9;
(6) 当xi与xj的影响程度介于上述五种情况的相邻两者之间时,取aij为两个判断值的平均,即2、4、6、8之一;
(7) 当xi与xj的影响之比aji取aij的倒数。
于是,得到第一级指标(第二层C1~C3)关于评价总目标层Z的比较判断矩阵Z-C和第二级指标(第三层C11~C33)关于第一指标的比较判断矩阵C1~C1j,C2~C2j,C3~C3j分别是


, 百拇医药
2.4 确定权重向量
由比较判断矩阵确定各指标因素的权重有多种方法,这里我们取矩阵的最大特征值λmax所对应的归一化的特征向量ω=(ω1,ω2,…,ωn)作为诸指标的权重向量。
基于求矩阵特征值和特征向量的困难,下面我们利用“求和法”近似计算比较判断矩阵的最大特征值和特征向量,其步骤是:
(1) 将比较判断矩阵A的列向量归一化得,
 ij=
ij=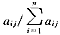 ;
;(2) 对
 ij按行求和得
ij按行求和得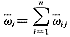 ;
;, http://www.100md.com
(3) 将
 i归一化
i归一化 ,即得近似特征向量ω=(ω1,ω2,…,ωn)T ;
,即得近似特征向量ω=(ω1,ω2,…,ωn)T ;(4) 计算
 ,作为最大特征值的近似值。其中(Aω)i是Aω的第i个分量。
,作为最大特征值的近似值。其中(Aω)i是Aω的第i个分量。定义
 作为衡量所得权重向量是否合理的指标,称CR为随机一致性比率,其中
作为衡量所得权重向量是否合理的指标,称CR为随机一致性比率,其中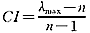 称为一致性指标,RI称为随机一致性指标(其具体数值由下表给出)。当
称为一致性指标,RI称为随机一致性指标(其具体数值由下表给出)。当 <0.1时,由上得到的归一化的特征向量即作为评价指标的权重向量。否则,说明比较判断矩阵不够合理,需要进行调整。这一步称为一致性检验。表1给出了用于判断的随机一致性指标RI的数值。
<0.1时,由上得到的归一化的特征向量即作为评价指标的权重向量。否则,说明比较判断矩阵不够合理,需要进行调整。这一步称为一致性检验。表1给出了用于判断的随机一致性指标RI的数值。, 百拇医药
表1 随机一致性指标RI的值 n
1
2
3
4
5
6
7
8
9
10
11
RI
0
, http://www.100md.com
0
0.58
0.90
1.12
1.24
1.32
1.41
1.45
1.49
1.51
其中n为比较判断矩阵的阶数。
现在利用“求和法”计算上面各个比较判断矩阵的权向量(这里略去具体的计算过程)为:
, http://www.100md.com
矩阵Z~Ci的权向量和最大特征值是:
ωz=(0.1061,0.2605,0.6334)T, λzmax=3.0386
按照一致性检验公式,分别计算一致性指标CIz和一致性比率CRz得:
CIz=0.0193,RIz=0.85,CRz=0.03<0.1
由于CRz=0.03<0.1,可见比较矩阵Z~Ci具有满意的一致性,所以由此得到的权向量是可行的,即C1,C2,C3关于Z的权重分别是0.1061,0.2605,0.6334。这说明对于综合考评来讲,一级指标层中的3项指标相对重要的是业务能力,其次是组织管理,最后是队伍结构。
, 百拇医药
类似可以得到其它三个矩阵的权向量、最大特征值、一致性指标和一致性比率分别是:
ωC1=(0.2,0.6,0.2)T, λC1maxmax=3
CIC1=0,RIC1=0.58,CRC1=0<0.1;
ωC2=(0.1165,0.1044,0.3895,0.3895)T, λC2maxmax=4.1935
, http://www.100md.com CIC2=0.0645,RIC2=0.9,CRC21=0.0716<0.1;
ωC3=(0.2518,0.5889,0.1593)T, λC3maxmax=3.0539
CIC3=0.027,RIC3=0.58,CRC3=0.0465<0.1。
各矩阵都通过了一致性的检验,如此我们得到了各子指标对于第二层每个指标的权重。为了得到这10项指标因素(Cij)对于综合考评这一总目标的权重(即给出层次总排序),按下列方法进行计算:
, http://www.100md.com
设一级指标层中3项指标因素C1,C2,C3的权重是a1,a2,a3,二级指标层中10项指标因素D1,D2,…,D10的权重分别是d1j,d2j,…,d10j,(j=1,2,3),(当Di与Cj无联系时记dij=0)。那么Di关于总目标Z的权重就是
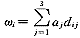 (i=1,2,…,10),于是,第二级指标层中10项指标因素的总排序即总的权向量是:
(i=1,2,…,10),于是,第二级指标层中10项指标因素的总排序即总的权向量是:ω=(ω1,ω2,…,ω10)T
, 百拇医药
层次总排序也要进行一致性检验,设二经指标层中某些指标对Cj单排序的一致性指标为CIj,随机一致性指标为RIj,则二级指标层总排序的随机一致性比率定义为:
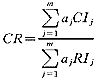
当CR<0.1时,认为层次总排序具有满意的程度。
现按此计算方法,求10项指标对于综合评价总目标的层次总排序,对于没有隶属影响的权值记为0,所得结果见表2。
表2 10项指标的权重总排序 第二层C
第三层D
C1
C2
, 百拇医药
C3
层次总
排序∑
0.1061
0.2605
0.6334
C11
0.2
0
0
0.0212
C12
, http://www.100md.com
0.6
0
0
0.0640
C13
0.2
0
0
0.0212
C21
0
0.1165
0
, 百拇医药
0.0303
C22
0
0.1044
0
0.0272
C23
0
0.3895
0
0.1015
C24
, 百拇医药
0
0.3895
0
0.1015
C31
0
0
0.2518
0.1599
C32
0
0
0.3730
, http://www.100md.com
0.3730
C33
0
0
0.1593
0.1009
进行总体一致性检验:

故
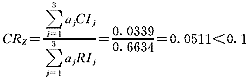
可见,得到的10项指标因素对于总评价目标的权向量是可接受的。于是,按照权重大小得到的10项指标因素相对于评价总目标重要程度的总排序是:
, 百拇医药
C32,C31,C23,C24,C33,C12,C13,C21,C11,C13
它们的权重分别由表2中右边一栏的数据给出。由上述过程可知,各项权重是对所有指标因素进行综合评判得到的,因此,具有较好的客观性和公正性。
由此可见,在10项考评指标中,相对重要的是第9项“对危重病人的抢救能力”、第8项“对疑难病症的诊治能力”、第6项“服务质量”、第7项“完成任务情况”、第10项“开拓创新能力”和第2项“业务与学术水平”。这里明显地体现了科室整体的专业能力、服务质量和完成任务情况。它们在综合评价中所占的权重分别是0.3730、0.1599、0.1015、0.1015、0.1009、0.064,占10项指标总权重的83.68%。
, http://www.100md.com
3 模型评述
3.1 对评价指标两两比较的结果,是由专家根据其客观经验确定的,可能会因不同的专家而异,可以请各专家分别给出比较结果,然后取其众数作为专家组一致的意见,但亦可采用其他方式,比如讨论协商等,达成一致的结果。
3.2 该模型给出了如何将评价的定性描述转化为定量分析的一般方法,并且算法也较为简单(通过简单的计算器即可完成),具有一般性,因此可以推广到许多类似的问题上去。
3.3 在实际使用中,各指标的权重只须取其两位有效数字即可。
3.4 对具体被评价的对象,应该就每一项指标按照五种比较强度标准建立相应的比较判断矩阵,计算各对象对每一指标的权重,最后计算各对象的层次总排序,但这不便于实际操作。因此,对每一项评价指标可以采取直接给评价对象打分,然后按上述权重计算加权平均,最后给出总排序就简单多了。■
参考文献:
[1] 王莲芬,许树柏.层次分析法引论.中国人民大学出版社,1990.
[2] 姜启源.数学模型(第二版).高等教育出版社,1997.
收稿日期:1999-03-22, 百拇医药