Fitzhugh-Nagumo神经传导方程的周期初值问题
作者：王慕洁 张仲
单位：王慕洁(哈尔滨医科大学 哈尔滨150086)； 张仲(哈尔滨医科大学 哈尔滨150086)
关键词：Fitzhugh-Nagumo方程；Galcrkin方法；Gronwall不等式
数理医药学杂志000106 摘 要：讨论了Fitzhugh-Nagumo方程的周期初值问题，用Galerkin方法证明了整体解的存在唯一性。
中图分类号：O 241.81
文章编号：1004-4337(2000)01-0013-02▲
1 引言
近年来人们对描述神经脉冲传导的Fitzhugh-Nagumo方程
, 百拇医药
ut=uxx+f(u)-v (1)
vt=σu-γv (2)
其中σ，γ>0是已知常数，f是已知实函数，进行了许多研究。如文献[1～4]讨论了方程行波解、周期平面波解的存在性，文献[5]讨论了方程初边值问题的整体存在性等。本文讨论方程(1)、(2)及其周期初值问题。
u(x+2D,t)=u(x,t),v(x+2D,t)=v(x,t) (3)
u(x,0)=u0(x),v(x,0)=v(x) (4)
我们用Galerkin方法证明了问题(1)～(4)整体解的存在唯一性。为了后面的讨论，我们先引入下面的记号：
, 百拇医药
令Ω=[0,2D],L2p(Ω)表示以2D为周期Ω上的平方可积函数空间，其内积和范数分别为：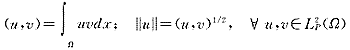
Hmp(Ω)表示以2D为周期的m阶Sobolev空间，用‖.‖m表示其范数。
2 主要结果及其证明
设{
k(x)}是问题
-kxx=λkk, k(x+2D)=k(x)
, http://www.100md.com
的特征函数所构成的规范正交完备系，N是任意正整数，SN=span{k(x)|k≤N},记问题(1)～(4)的近似解为：
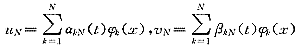
那么由Galerkin方法，uN,vN应满足下面的常微分方程组
(uNt-uNxx-f(uN)+vN,)=0; (5)
(vNt+γvN-σuN,)=0, 
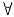
∈SN (6)
, http://www.100md.com
αkN(0)=akN,βkN(0)=bkN,k≤N (7)
初值akN,bkN的选择应该使得在空间H1p(Ω)中有
uN(0)→u0,vN(0)→v0,当N→+∞时 (8)
由常微分方程理论，方程组(5)～(7)存在唯一局部解uN,vN。下面我们对uN,vN作一致的先验估计。
引理1 假设f∈c2,f(0)=0,f′(0)=-a<0,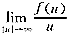
=-∞,那么对近似解uN,vN有下面的估计式成立：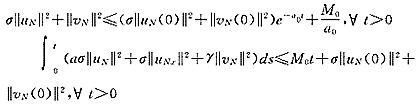
, http://www.100md.com
其中a0,M0是与N无关的常数。
证明 在(5)式中令=σuN,在(6)式中令=vN，相加有
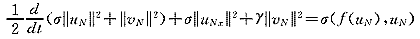(9)
由对f的假设可知f可写成f(u)=-au+u2f1(u),并且
于是uf1(u)的上确界M1≥0,且存在常数M2>0，使得当‖u‖≥M2时，uf1(u)≤0。因此有
, 百拇医药
(f(uN),uN)=-a‖uN‖2+(uNf1(uN),u2N)≤-a‖uN‖2+2DM1M22
将上式代入(9)式并记M0=4DM1M22有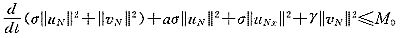
(10)
令a0=min{a,γ},对(10)式用Gronwall不等式可得引理中第一式，再直接对(10)式积分即完成引理证明。
, 百拇医药 引理2 假设引理1的条件成立，且|f1(u)|≤A|u|+B,那么对问题(4)～(6)的解uN,vN有下面的估计式
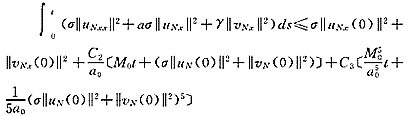
其中Ci是只与A、B、D、σ有关的常数。
证明 在(5)式中令=-σuNxx,在(6)式中令=-vNxx,并利用琴生不等式和Sobolev不等式有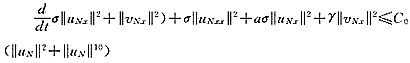
, http://www.100md.com
对上式用Gronwall不等式并利用引理1的结果即完成本引理的证明。
注意到上面估计式中的各常数均与N无关，因此由紧致性原理立即有：
定理1 假设引理2的条件成立，且u0,v0∈H1p(Ω),那么问题(1)～(4)存在整体解u(x,t)和v(x,t)，并且
u∈L∞(R+;H1p(Ω))∩L2(0,T;H2p(Ω)),v∈L∞(R+;H1p(Ω))∩L2(0,T;H1p(Ω))。
, 百拇医药
推论 在定理1的假设下有
‖u‖∞+‖v‖∞≤c,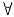t>0
其中c是与‖u0‖1,‖v0‖1有关与t无关的常数。
定理2 在定理2.1的条件下，问题(1)～(4)的整体解是唯一的。
证明 设u1,v1和u2,v2都是问题(1)～(4)的解，令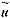
=u1-u2, 
=v1-v2,则有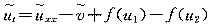
(11)
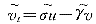(12)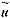(x,0)=(x,0)=0 (13)
, 百拇医药
用σ(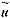-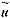xx),-xx分别与(11)，(12)式作内积有
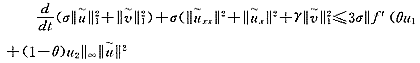
由Gronwall不等式和(13)式有
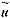‖‖21+‖‖21=0, t>0
, 百拇医药
进面有
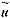‖xx‖2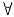=0, t>0
这就证明了问题(1)～(4)的整体解是唯一的。■
参考文献：
[1] B.D.Sleeman, Small Amplitude Periodic Waves for the Fitzhugh-Nagumo Equations, J.Math. Biol., 1982,14:309～325.
[2] J.Rinzel, Repetitive Activitg and Bifurcation Under Point Stimulation For a Simple Fitzhugh-Nagumo Nerve Conduction Model, J.Math Biol, 1978,5:363～382.
[3] M.E.Schorbeck, Boundary Value Problems for the Fitzhugh-Nagumo Equations, J. Diff Equa, 1978,30:119～147.
[4] 刘宝平，赵壁.Fitzhugh-Nagumo神经传导方程的多重周期平面波解.应用数学学报，1989，12：13～23.
[5] 郑宋穆，沈玮熙.Fitzhugh-Nagumo方程组初边值问题的整体存在性.科学通报，1984，16，966～969.
收稿日期：1999-02-20, http://www.100md.com
单位：王慕洁(哈尔滨医科大学 哈尔滨150086)； 张仲(哈尔滨医科大学 哈尔滨150086)
关键词：Fitzhugh-Nagumo方程；Galcrkin方法；Gronwall不等式
数理医药学杂志000106 摘 要：讨论了Fitzhugh-Nagumo方程的周期初值问题，用Galerkin方法证明了整体解的存在唯一性。
中图分类号：O 241.81
文章编号：1004-4337(2000)01-0013-02▲
1 引言
近年来人们对描述神经脉冲传导的Fitzhugh-Nagumo方程
, 百拇医药
ut=uxx+f(u)-v (1)
vt=σu-γv (2)
其中σ，γ>0是已知常数，f是已知实函数，进行了许多研究。如文献[1～4]讨论了方程行波解、周期平面波解的存在性，文献[5]讨论了方程初边值问题的整体存在性等。本文讨论方程(1)、(2)及其周期初值问题。
u(x+2D,t)=u(x,t),v(x+2D,t)=v(x,t) (3)
u(x,0)=u0(x),v(x,0)=v(x) (4)
我们用Galerkin方法证明了问题(1)～(4)整体解的存在唯一性。为了后面的讨论，我们先引入下面的记号：
, 百拇医药
令Ω=[0,2D],L2p(Ω)表示以2D为周期Ω上的平方可积函数空间，其内积和范数分别为：
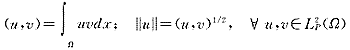
Hmp(Ω)表示以2D为周期的m阶Sobolev空间，用‖.‖m表示其范数。
2 主要结果及其证明
设{
k(x)}是问题-
kxx=λkk, k(x+2D)=k(x), http://www.100md.com
的特征函数所构成的规范正交完备系，N是任意正整数，SN=span{
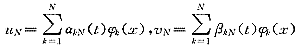
k(x)|k≤N},记问题(1)～(4)的近似解为：那么由Galerkin方法，uN,vN应满足下面的常微分方程组
(uNt-uNxx-f(uN)+vN,
)=0; (5)(vNt+γvN-σuN,
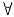
)=0, ∈SN (6), http://www.100md.com
αkN(0)=akN,βkN(0)=bkN,k≤N (7)
初值akN,bkN的选择应该使得在空间H1p(Ω)中有
uN(0)→u0,vN(0)→v0,当N→+∞时 (8)
由常微分方程理论，方程组(5)～(7)存在唯一局部解uN,vN。下面我们对uN,vN作一致的先验估计。
引理1 假设f∈c2,f(0)=0,f′(0)=-a<0,
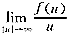=-∞,那么对近似解uN,vN有下面的估计式成立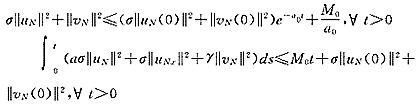：, http://www.100md.com
其中a0,M0是与N无关的常数。
证明 在(5)式中令
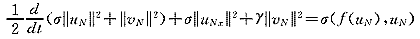=σuN,在(6)式中令=vN，相加有 (9)由对f的假设可知f可写成f(u)=-au+u2f1(u),并且
于是uf1(u)的上确界M1≥0,且存在常数M2>0，使得当‖u‖≥M2时，uf1(u)≤0。因此有
, 百拇医药
(f(uN),uN)=-a‖uN‖2+(uNf1(uN),u2N)≤-a‖uN‖2+2DM1M22
将上式代入(9)式并记M0=4DM1M22有
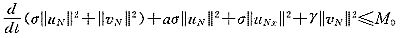(10)令a0=min{a,γ},对(10)式用Gronwall不等式可得引理中第一式，再直接对(10)式积分即完成引理证明。
, 百拇医药 引理2 假设引理1的条件成立，且|f1(u)|≤A|u|+B,那么对问题(4)～(6)的解uN,vN有下面的估计式
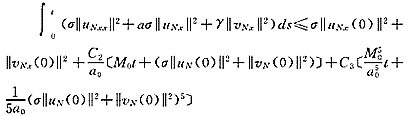
其中Ci是只与A、B、D、σ有关的常数。
证明 在(5)式中令
=-σuNxx,在(6)式中令=-vNxx,并利用琴生不等式和Sobolev不等式有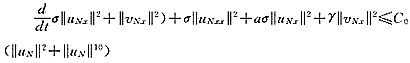, http://www.100md.com
对上式用Gronwall不等式并利用引理1的结果即完成本引理的证明。
注意到上面估计式中的各常数均与N无关，因此由紧致性原理立即有：
定理1 假设引理2的条件成立，且u0,v0∈H1p(Ω),那么问题(1)～(4)存在整体解u(x,t)和v(x,t)，并且
u∈L∞(R+;H1p(Ω))∩L2(0,T;H2p(Ω)),v∈L∞(R+;H1p(Ω))∩L2(0,T;H1p(Ω))。
, 百拇医药
推论 在定理1的假设下有
‖u‖∞+‖v‖∞≤c,
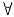t>0其中c是与‖u0‖1,‖v0‖1有关与t无关的常数。
定理2 在定理2.1的条件下，问题(1)～(4)的整体解是唯一的。
证明 设u1,v1和u2,v2都是问题(1)～(4)的解，令
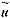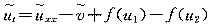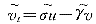=u1-u2, =v1-v2,则有 (11) (12)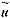(x,0)=(x,0)=0 (13), 百拇医药
用σ(
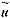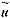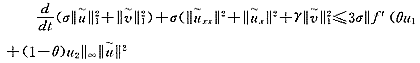
-xx),-xx分别与(11)，(12)式作内积有由Gronwall不等式和(13)式有
‖
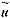‖21+‖‖21=0, t>0, 百拇医药
进面有
‖
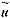xx‖2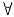=0, t>0这就证明了问题(1)～(4)的整体解是唯一的。■
参考文献：
[1] B.D.Sleeman, Small Amplitude Periodic Waves for the Fitzhugh-Nagumo Equations, J.Math. Biol., 1982,14:309～325.
[2] J.Rinzel, Repetitive Activitg and Bifurcation Under Point Stimulation For a Simple Fitzhugh-Nagumo Nerve Conduction Model, J.Math Biol, 1978,5:363～382.
[3] M.E.Schorbeck, Boundary Value Problems for the Fitzhugh-Nagumo Equations, J. Diff Equa, 1978,30:119～147.
[4] 刘宝平，赵壁.Fitzhugh-Nagumo神经传导方程的多重周期平面波解.应用数学学报，1989，12：13～23.
[5] 郑宋穆，沈玮熙.Fitzhugh-Nagumo方程组初边值问题的整体存在性.科学通报，1984，16，966～969.
收稿日期：1999-02-20, http://www.100md.com