基于Iwao -m生态模型的疾病空间分布动态模型—疾病的空间分布动态模型研究(二)
作者:薛付忠 王洁贞
单位:薛付忠(山东医科大学公共卫生学院 济南250072); 王洁贞(山东医科大学公共卫生学院 济南250072)
关键词:
数理医药学杂志000102
中图分类号:Q 141
文章编号:1004-4337(2000)01-0003-03▲
在生态学研究中,Iwao在1968、1969年所描述的生物种群空间分布图式为[1~3,5]: =α+βm,其中m~为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解放。本文根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
=α+βm,其中m~为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解放。本文根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
, 百拇医药
我们的流行病学假设是:在某一特定生境内的某病病例,其空间分布格局指标可以由病例平均密度mc(case density)平均拥挤度及 c(case cowding)来描述。定义如下:
c(case cowding)来描述。定义如下:
当样本含量较大时有近似形式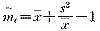
 c的第一种形式反映对于每个个体,在同一样方(即样本单位)中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数;或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。
c的第一种形式反映对于每个个体,在同一样方(即样本单位)中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数;或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。 c的第二种形式则直观地反映了
c的第二种形式则直观地反映了 c与病例空间格局的关系,因为在随机格局中s2
c与病例空间格局的关系,因为在随机格局中s2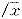 =1,故有
=1,故有 c=
c=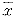 。于是有:
。于是有: c
c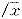 =1,为随机格局;
=1,为随机格局; c
c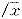 <1,为均匀格局;
<1,为均匀格局; c
c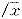 >1,为聚集格局。
>1,为聚集格局。 c
c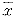 刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与
刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与 c
c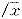 间的函数关系,则能定量反映疾病聚集动态的变化规律。
间的函数关系,则能定量反映疾病聚集动态的变化规律。
, 百拇医药
这里我们的假设是病例的平均拥挤度 c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。
c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。
1 建模方法及其模型参数的流行病学含义
在以上假设的基础上,根据 c和mc的含义以及疾病的流行病学特点,我们提出以下模型:
c和mc的含义以及疾病的流行病学特点,我们提出以下模型: c=α+β1mc+β2m2c+β3m3c+…+βkmkc
c=α+β1mc+β2m2c+β3m3c+…+βkmkc
, http://www.100md.com
一般情况下,取 c的3次模型便可以达到拟合精度:
c的3次模型便可以达到拟合精度: c=α+βmc+γm2c+δm3c
c=α+βmc+γm2c+δm3c
模型中参数的流行病学含义为:
① α是每个基本成分中个体数分布的平均拥挤度,称为基本聚集度指标:
α=0,分布的基本成分是单个个体,病例间没有相互内在联系,既不相互排斥也不相互吸引;
α>0,分布的基本成分是个群体,病例间存在着某种内在联系,病例间相互吸引;
, 百拇医药
α<0,病例间存在相互排斥的内在联系特点。
② β表示基本成分的空间格局,体现了基本成分的相对聚集度,称为密度-聚集度指标:
β=0,病例的空间格局为随机分布;
β<1,病例的空间格局为均匀分布,β越小分布越均匀;
β>0,病例的空间格局为聚集分布,β越大分布越聚集。
③ γ+2δm是基本成分的相对聚集度随病例平均密度而变化的速率;
④ 2δ是基本成分的相对聚集度随病例平均密度变化的加速率。
这是因为我们假定β随mc变化的速率不只是一个常数,而是与mc有关的,因为病例平均密度变大时,相对聚集度β变化的速率也随之变大,因此设:
, 百拇医药
β=f(mc)=β′+γmc+δm2c,f′(x)=γ+2δmc,f″(x)=2δ
用同样的方法可以定义更高阶的模型参数的流行病学含义。
⑤ 当病例密度足够低时,模型中右端第四项m3c为高阶无穷小,可以忽略,即相当于不考虑加速度,δ=0,这时模型为: c=α+βmc+γm2c。
c=α+βmc+γm2c。
⑥ 当右端的m2c也看成是无穷小时,则m2c也可以忽略,即相当于不考虑速率,γ=0,这时模型为: c=α+βmc,也就是Iwao的原模型。
c=α+βmc,也就是Iwao的原模型。
, http://www.100md.com
⑦ 若 c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对
c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对 c实施对数变换,则模型变为:
c实施对数变换,则模型变为:
Ln( c)=α+β1mc+β2m2c+β3m3c+…+βkmkc
c)=α+β1mc+β2m2c+β3m3c+…+βkmkc
同样根据以上方法确定模型参数的流行病学含义。
, http://www.100md.com
⑧ 评价模型拟合优度的指标我们定义为偏离度(B,Bias):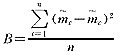
其中, c为模型计算所得的平均拥挤度的估计值。
c为模型计算所得的平均拥挤度的估计值。
⑨ 病例空间结构特点的表达:
以聚块性指标 c/mc为因变量,以密度mc为自变量,建立回归模型,它们的回归关系一般不是线性的,可试用指数曲线、对数曲线、幂曲线、多项式曲线等拟合,以观察密度mc随聚块性指标
c/mc为因变量,以密度mc为自变量,建立回归模型,它们的回归关系一般不是线性的,可试用指数曲线、对数曲线、幂曲线、多项式曲线等拟合,以观察密度mc随聚块性指标 c/mc动态变化的趋势。
c/mc动态变化的趋势。
, http://www.100md.com
⑩病例个体群范围的量化:
对于特定的微小生境(由一个自然村或几个自然村组成),用不同大小的样方单位面积,多次对其划定网络,按样方单位面积梯度以聚块性指标 c/mc为因变量,以样方面积为自变量做曲线图,
c/mc为因变量,以样方面积为自变量做曲线图, c/mc曲线下降最陡时所对应的样方面积大小,或
c/mc曲线下降最陡时所对应的样方面积大小,或 c/mc-样方单位面积曲线模型的一阶导数取得最大值时,所对应的样方面积大小,就相当于病例个体群(即基本成分)的面积;还可以在时间维上分别作
c/mc-样方单位面积曲线模型的一阶导数取得最大值时,所对应的样方面积大小,就相当于病例个体群(即基本成分)的面积;还可以在时间维上分别作 c/mc-样方单位面积曲线图或拟合模型,找出不同时间病例个体群的面积。对传染病来说,个体群面积反映了传染源的活动面积范围,这对划定疫点范围具有重要的指导意义。
c/mc-样方单位面积曲线图或拟合模型,找出不同时间病例个体群的面积。对传染病来说,个体群面积反映了传染源的活动面积范围,这对划定疫点范围具有重要的指导意义。
, http://www.100md.com
2 模型解法
根据最小二乘法原理,采用一般多项式曲线拟合的SAS程序建立模型和优选模型,或用逐步回归方法进行模型优选[7]:
将模型通过变量变换转化为多元线性回归问题,即设z1=mc,z2=m2c,z3=m3c,…,zk=mkc,就把模型转化为多元线性回归方程:
z=α+β1z1+β2z2+…+βkzk
调用SAS软件中的REG过程便可完成建模和模型优选。
, 百拇医药
3 实例分析
现以山东省平邑县1997年肾综合征出血热(HRFS)空间分布资料为例说明建模过程:该县处于山东临沂市,为全国HRFS重点发病县,1997年发病率高达106.24/10万。县内地理生态环境复杂,山区、丘岭、平原、库区、涝洼交错布局,且各地植被、鼠类种群分布各异。为此,根据地理生态环境特点,打破乡(镇)间的行政界限将全县划为14个生境区进行分析。
3.1 网格的划定和自然村的标化
由于HRFS的空间分布与自然村的分布有关,因而在划定网格(即样本单位)时必须设法消除自然村的影响。我们巧妙地采取了一种特殊的技术措施使自然村成为均匀分布:即①、设定正方形网格的大小与最大自然村的面积相等;②、抽取生境区时,尽量使自然村的网格内的分布均匀;③、经①、②处理后仍有部分自然村具有极强的聚集性,这时,如果一个网格内的自然村数在5个以上时,则将它们看作为一个自然村。通过这三步处理就使自然村达到了均匀分布(见表1)。
, http://www.100md.com
表1 平邑县自然村和1997年肾综合征出血热空间分布基本参数 生境区域
自然村空间分布参数
肾综合征出血热空间分布参数
mc c
c c/mc
c/mc
s2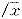
mc c
c c/mc
c/mc
, 百拇医药
s2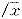
1
1.0261
1.0885
1.0608
1.0625
0.5479
1.3503
2.4641
1.8022
2
, 百拇医药
1.1343
1.1359
1.0014
1.1816
0.6377
5.3632
8.4102
5.7255
3
1.2911
0.8627
0.6682
0.5716
, 百拇医药
1.5488
4.2992
2.7758
3.7504
4
1.0857
0.6053
0.5575
0.5196
2.6806
6.3936
2.3851
4.7130
, http://www.100md.com
5
1.1563
0.6217
0.5377
0.4653
2.1176
5.1529
2.4334
4.0353
6
1.3012
0.9630
0.7401
, 百拇医药
0.6618
0.9762
2.9754
3.0480
2.9992
7
1.3448
0.7692
0.5720
0.4244
0.7627
4.4047
5.7751
, 百拇医药
4.6820
8
1.6667
1.0858
0.6515
0.9191
1.3881
4.3869
3.1604
3.9988
9
1.9545
1.7441
, 百拇医药
0.8924
0.7896
0.5238
2.4545
4.6860
2.9307
10
1.3281
1.2235
0.9214
0.8954
0.3333
, 百拇医药 1.5654
4.6967
2.2321
11
2.3261
1.8609
0.8000
0.5348
1.3571
4.2456
3.1284
3.8885
12
, 百拇医药
2.4000
2.0417
0.8507
0.6417
0.7000
1.7429
2.3470
1.9429
13
2.3721
2.0784
0.8762
, 百拇医药 0.7063
0.6364
1.9286
3.0305
2.2922
14
1.8684
1.5493
0.8292
0.6809
0.3256
0.5414
1.7549
, 百拇医药
1.2458
自然村空间分布的数学模型:根据以上设定网格的方法,抽取了14个生境区,计算各区内自然村的mc、 c、
c、 c/mc、s2
c/mc、s2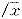 见表1。
见表1。
由表1可见自然村的 c/mc、s
c/mc、s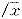 ,1、2区接近于1,其它区都小于1,基本达到了均匀分布。其空间分布动态模型为:
,1、2区接近于1,其它区都小于1,基本达到了均匀分布。其空间分布动态模型为: c=-0.2130+0.9267mc γ=0.9178,P=0.0001
c=-0.2130+0.9267mc γ=0.9178,P=0.0001
, 百拇医药
其F=64.155,P=0.0001;tα=-1.112,P=0.2878;tβ=8.010,P=0.0001。
在0.05水平上回归方程及回归系数均有极显著性;B=0.0378,说明模型拟合极佳。因α=-0.2130,而P=0.2827>0.05,所以总体α为0,自然村分布的基本成分是单个个体;又β<0,所以自然村的空间格局是均匀分布。在此水平上研究HRFS的空间格局就消除了自然村的影响。
2.2 不同生境内的HRFS病例空间分布格局分析结果
由表1可见,HRFS的 c/mc、s2
c/mc、s2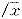 均大于1,说明其有明显的聚集性。进一步根据不同的生境特点做回归分析,其结果如下:
均大于1,说明其有明显的聚集性。进一步根据不同的生境特点做回归分析,其结果如下:
, 百拇医药
① 将全县看作一个特定生境(共14个生境区):
空间格局模型: c=1.2476+2.0135mc,γ=0.7915,P=0.0007;
c=1.2476+2.0135mc,γ=0.7915,P=0.0007;
模型检验:F=20.132,P=0.0007;tα=2.245,p=0.0444;tβ=4.487,p=0.0007;
模型精度:B=1.1000。
② 平原地带
生境特点:该区由3、4、5、6、7、11区组成,为平原,主要作物为小麦、玉米,境内的自然村一般较大。
, 百拇医药 空间格局模型: c=2.4466+1.3546mc,γ=0.8597,P=0.0281;
c=2.4466+1.3546mc,γ=0.8597,P=0.0281;
模型检验:F=11.333,P=0.0281;tα=3.566,p=0.0235;tβ=3.366,p=0.0281;
模型精度:B=0.6467。
③ 山区干旱地带
生境特点:该区由1、8、9、10、12、13、14区组成,为山区干旱地带,主要作物地瓜、花生、以秋季作物为主。
空间格局模型: c=0.0605+3.0249mc,γ=0.9053,P=0.005;
c=0.0605+3.0249mc,γ=0.9053,P=0.005;
, 百拇医药
模型检验:F=22.705,P=0.005;tα=0.133,p=0.9886;tβ=4.765,p=0.005;
模型精度:B=0.2240。
④ 涝洼、库区
生境特点:该区由2、3、4、5、7、8、11组成,其中2、3、4、5、7为平原区中涝洼较多的地带,8、11虽为山区、丘陵,但内有唐村、昌里两大水库位于其中。
空间格局模型: c=6.6753+3.3743mc+1.2273m2c,R2=0.9120;
c=6.6753+3.3743mc+1.2273m2c,R2=0.9120;
, 百拇医药
模型检验:F=20.736,P=0.0077;tα=11.151,p=0.0004;tβ=4.160,p=0.0141;tγ=5.047,p=0.0072;
模型精度:B=0.0366。
由此可见,以全县为一大的生境时,α>0,HRFS病例的基本成分是群体,病例间存在某种流行病学联系;β>0,HRFS病例呈聚集分布。而按不同生境分别分析时,却各有特点:平原和涝洼、库区α值都较大,分别为2.4466、6.6753,病例间有较强的联系;它们的β的绝对值都大于1,分别为1.3546、3.3743,病例分布具有较高聚集性,且涝洼、库区的联系性和聚集性均大于平原。对于山区干旱地带,α为0.0605,P>0.05,所以病例的基本成分是个体,没有流行病学联系;而β为3.0249,表明病例的聚集性也较强。充分体现了HRFS在不同生境内的空间分布特点。关于 c/mc和mc关系分布和疫点范围量化,限于篇幅将另文讨论。模型还可用于研究时间维上的某一特定生境内HRFS病例的空间分布动态规律,即对于某一特定生境,计算其内不同的时间HRFS病例分布的
c/mc和mc关系分布和疫点范围量化,限于篇幅将另文讨论。模型还可用于研究时间维上的某一特定生境内HRFS病例的空间分布动态规律,即对于某一特定生境,计算其内不同的时间HRFS病例分布的 c与mc,建立模型,以反映该特定生境内HRFS病例的空间分布随时间的变化规律。模型揭示对于平原和涝洼、库区在重点抓好病例聚集区内的灭鼠防病时,应注重发病“灶点”的处理;而对于平原干旱地带则不易采取“灶点”处理,而应当对整个病例聚集区采取措施。同时,提示我们对于HRFS的防治不能一刀切地搞“大面积灭鼠”,而必须因地制宜地根据其所处的生境特点采取相应的措施。■
c与mc,建立模型,以反映该特定生境内HRFS病例的空间分布随时间的变化规律。模型揭示对于平原和涝洼、库区在重点抓好病例聚集区内的灭鼠防病时,应注重发病“灶点”的处理;而对于平原干旱地带则不易采取“灶点”处理,而应当对整个病例聚集区采取措施。同时,提示我们对于HRFS的防治不能一刀切地搞“大面积灭鼠”,而必须因地制宜地根据其所处的生境特点采取相应的措施。■
, http://www.100md.com
参考文献:
[1] Iwao,S and Kuno, E.Use of the regression of mean crowding on mean density for estimating sample size and the transformation of data for the analysis of variance. Res. Popul Ecol. 1984,210~214.
[2] Iwao, S. and Kuno, E:An approach to the analysis of aggregation patterns in biological populations. Statistical Ecology.1, 461~513,Penn State Univ. Press. 1971.
[3] Iwao,S: Application of the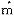 -m method to the analysis of spatial pattern by changing the quadrat sine. Res. Popul. Ecol. 1972,14(1):79~128.
-m method to the analysis of spatial pattern by changing the quadrat sine. Res. Popul. Ecol. 1972,14(1):79~128.
, http://www.100md.com
[4] 蔡晓明等.大白菜上七星瓢虫空间格局及抽样技术研究生态学杂志,1991,10(5):6~11.
[5] Iwao S. A new regression method for analysis the aggregation pattern of animal populations Res. Popul.Ecol. 1968,10(1):1~20.
[6] 徐汝梅等.改正的Iwao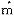 -m模型.生态学报,1984,4(2):111~118.
-m模型.生态学报,1984,4(2):111~118.
[7] 胡良平.现代统计学与SAS应用.军事医学科学出版社,1996,215~265.
收稿日期:1999-03-09, 百拇医药
单位:薛付忠(山东医科大学公共卫生学院 济南250072); 王洁贞(山东医科大学公共卫生学院 济南250072)
关键词:
数理医药学杂志000102
中图分类号:Q 141
文章编号:1004-4337(2000)01-0003-03▲
在生态学研究中,Iwao在1968、1969年所描述的生物种群空间分布图式为[1~3,5]:
 =α+βm,其中m~为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解放。本文根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。
=α+βm,其中m~为种群平均拥挤度,m为平均密度,并且对α,β的生物学含义作出了明确的解放。本文根据这些生态学研究的基本思想,提出适合描述疾病空间动态的基本流行病学假设,并据此假设建立相应的数学模型,定量地刻划其空间分布动态。, 百拇医药
我们的流行病学假设是:在某一特定生境内的某病病例,其空间分布格局指标可以由病例平均密度mc(case density)平均拥挤度及
 c(case cowding)来描述。定义如下:
c(case cowding)来描述。定义如下:
当样本含量较大时有近似形式
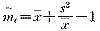
 c的第一种形式反映对于每个个体,在同一样方(即样本单位)中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数;或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。
c的第一种形式反映对于每个个体,在同一样方(即样本单位)中有多少其它个体的平均数,即每个个体在它样方中“邻居”的平均数;或者说是平均每个个体有多少在同单位内的其它个体,可以认为这些个体是与第一个个体共占一个单位。 c的第二种形式则直观地反映了
c的第二种形式则直观地反映了 c与病例空间格局的关系,因为在随机格局中s2
c与病例空间格局的关系,因为在随机格局中s2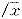 =1,故有
=1,故有 c=
c=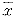 。于是有:
。于是有: c
c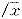 =1,为随机格局;
=1,为随机格局; c
c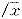 <1,为均匀格局;
<1,为均匀格局; c
c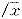 >1,为聚集格局。
>1,为聚集格局。 c
c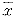 刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与
刻划了病例空间格局的内在性质,反映了其在一定条件下的聚集状态的变化。如果在时间维上,建立时间t与 c
c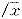 间的函数关系,则能定量反映疾病聚集动态的变化规律。
间的函数关系,则能定量反映疾病聚集动态的变化规律。, 百拇医药
这里我们的假设是病例的平均拥挤度
 c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。
c与其平均密度mc间存在着某种线性或非线性关系,而这种线性或非线性关系则体现了病例的空间分布动态机制,进而反映其流行病学机制。1 建模方法及其模型参数的流行病学含义
在以上假设的基础上,根据
 c和mc的含义以及疾病的流行病学特点,我们提出以下模型:
c和mc的含义以及疾病的流行病学特点,我们提出以下模型: c=α+β1mc+β2m2c+β3m3c+…+βkmkc
c=α+β1mc+β2m2c+β3m3c+…+βkmkc, http://www.100md.com
一般情况下,取
 c的3次模型便可以达到拟合精度:
c的3次模型便可以达到拟合精度: c=α+βmc+γm2c+δm3c
c=α+βmc+γm2c+δm3c模型中参数的流行病学含义为:
① α是每个基本成分中个体数分布的平均拥挤度,称为基本聚集度指标:
α=0,分布的基本成分是单个个体,病例间没有相互内在联系,既不相互排斥也不相互吸引;
α>0,分布的基本成分是个群体,病例间存在着某种内在联系,病例间相互吸引;
, 百拇医药
α<0,病例间存在相互排斥的内在联系特点。
② β表示基本成分的空间格局,体现了基本成分的相对聚集度,称为密度-聚集度指标:
β=0,病例的空间格局为随机分布;
β<1,病例的空间格局为均匀分布,β越小分布越均匀;
β>0,病例的空间格局为聚集分布,β越大分布越聚集。
③ γ+2δm是基本成分的相对聚集度随病例平均密度而变化的速率;
④ 2δ是基本成分的相对聚集度随病例平均密度变化的加速率。
这是因为我们假定β随mc变化的速率不只是一个常数,而是与mc有关的,因为病例平均密度变大时,相对聚集度β变化的速率也随之变大,因此设:
, 百拇医药
β=f(mc)=β′+γmc+δm2c,f′(x)=γ+2δmc,f″(x)=2δ
用同样的方法可以定义更高阶的模型参数的流行病学含义。
⑤ 当病例密度足够低时,模型中右端第四项m3c为高阶无穷小,可以忽略,即相当于不考虑加速度,δ=0,这时模型为:
 c=α+βmc+γm2c。
c=α+βmc+γm2c。⑥ 当右端的m2c也看成是无穷小时,则m2c也可以忽略,即相当于不考虑速率,γ=0,这时模型为:
 c=α+βmc,也就是Iwao的原模型。
c=α+βmc,也就是Iwao的原模型。, http://www.100md.com
⑦ 若
 c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对
c与mc的k次方间仍不呈线性,则可以对它实施变量变换,使其达到线性化的要求。例如对 c实施对数变换,则模型变为:
c实施对数变换,则模型变为:Ln(
 c)=α+β1mc+β2m2c+β3m3c+…+βkmkc
c)=α+β1mc+β2m2c+β3m3c+…+βkmkc同样根据以上方法确定模型参数的流行病学含义。
, http://www.100md.com
⑧ 评价模型拟合优度的指标我们定义为偏离度(B,Bias):
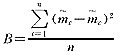
其中,
 c为模型计算所得的平均拥挤度的估计值。
c为模型计算所得的平均拥挤度的估计值。⑨ 病例空间结构特点的表达:
以聚块性指标
 c/mc为因变量,以密度mc为自变量,建立回归模型,它们的回归关系一般不是线性的,可试用指数曲线、对数曲线、幂曲线、多项式曲线等拟合,以观察密度mc随聚块性指标
c/mc为因变量,以密度mc为自变量,建立回归模型,它们的回归关系一般不是线性的,可试用指数曲线、对数曲线、幂曲线、多项式曲线等拟合,以观察密度mc随聚块性指标 c/mc动态变化的趋势。
c/mc动态变化的趋势。, http://www.100md.com
⑩病例个体群范围的量化:
对于特定的微小生境(由一个自然村或几个自然村组成),用不同大小的样方单位面积,多次对其划定网络,按样方单位面积梯度以聚块性指标
 c/mc为因变量,以样方面积为自变量做曲线图,
c/mc为因变量,以样方面积为自变量做曲线图, c/mc曲线下降最陡时所对应的样方面积大小,或
c/mc曲线下降最陡时所对应的样方面积大小,或 c/mc-样方单位面积曲线模型的一阶导数取得最大值时,所对应的样方面积大小,就相当于病例个体群(即基本成分)的面积;还可以在时间维上分别作
c/mc-样方单位面积曲线模型的一阶导数取得最大值时,所对应的样方面积大小,就相当于病例个体群(即基本成分)的面积;还可以在时间维上分别作 c/mc-样方单位面积曲线图或拟合模型,找出不同时间病例个体群的面积。对传染病来说,个体群面积反映了传染源的活动面积范围,这对划定疫点范围具有重要的指导意义。
c/mc-样方单位面积曲线图或拟合模型,找出不同时间病例个体群的面积。对传染病来说,个体群面积反映了传染源的活动面积范围,这对划定疫点范围具有重要的指导意义。, http://www.100md.com
2 模型解法
根据最小二乘法原理,采用一般多项式曲线拟合的SAS程序建立模型和优选模型,或用逐步回归方法进行模型优选[7]:
将模型通过变量变换转化为多元线性回归问题,即设z1=mc,z2=m2c,z3=m3c,…,zk=mkc,就把模型转化为多元线性回归方程:
z=α+β1z1+β2z2+…+βkzk
调用SAS软件中的REG过程便可完成建模和模型优选。
, 百拇医药
3 实例分析
现以山东省平邑县1997年肾综合征出血热(HRFS)空间分布资料为例说明建模过程:该县处于山东临沂市,为全国HRFS重点发病县,1997年发病率高达106.24/10万。县内地理生态环境复杂,山区、丘岭、平原、库区、涝洼交错布局,且各地植被、鼠类种群分布各异。为此,根据地理生态环境特点,打破乡(镇)间的行政界限将全县划为14个生境区进行分析。
3.1 网格的划定和自然村的标化
由于HRFS的空间分布与自然村的分布有关,因而在划定网格(即样本单位)时必须设法消除自然村的影响。我们巧妙地采取了一种特殊的技术措施使自然村成为均匀分布:即①、设定正方形网格的大小与最大自然村的面积相等;②、抽取生境区时,尽量使自然村的网格内的分布均匀;③、经①、②处理后仍有部分自然村具有极强的聚集性,这时,如果一个网格内的自然村数在5个以上时,则将它们看作为一个自然村。通过这三步处理就使自然村达到了均匀分布(见表1)。
, http://www.100md.com
表1 平邑县自然村和1997年肾综合征出血热空间分布基本参数 生境区域
自然村空间分布参数
肾综合征出血热空间分布参数
mc
 c
c c/mc
c/mcs2
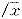
mc
 c
c c/mc
c/mc, 百拇医药
s2
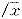
1
1.0261
1.0885
1.0608
1.0625
0.5479
1.3503
2.4641
1.8022
2
, 百拇医药
1.1343
1.1359
1.0014
1.1816
0.6377
5.3632
8.4102
5.7255
3
1.2911
0.8627
0.6682
0.5716
, 百拇医药
1.5488
4.2992
2.7758
3.7504
4
1.0857
0.6053
0.5575
0.5196
2.6806
6.3936
2.3851
4.7130
, http://www.100md.com
5
1.1563
0.6217
0.5377
0.4653
2.1176
5.1529
2.4334
4.0353
6
1.3012
0.9630
0.7401
, 百拇医药
0.6618
0.9762
2.9754
3.0480
2.9992
7
1.3448
0.7692
0.5720
0.4244
0.7627
4.4047
5.7751
, 百拇医药
4.6820
8
1.6667
1.0858
0.6515
0.9191
1.3881
4.3869
3.1604
3.9988
9
1.9545
1.7441
, 百拇医药
0.8924
0.7896
0.5238
2.4545
4.6860
2.9307
10
1.3281
1.2235
0.9214
0.8954
0.3333
, 百拇医药 1.5654
4.6967
2.2321
11
2.3261
1.8609
0.8000
0.5348
1.3571
4.2456
3.1284
3.8885
12
, 百拇医药
2.4000
2.0417
0.8507
0.6417
0.7000
1.7429
2.3470
1.9429
13
2.3721
2.0784
0.8762
, 百拇医药 0.7063
0.6364
1.9286
3.0305
2.2922
14
1.8684
1.5493
0.8292
0.6809
0.3256
0.5414
1.7549
, 百拇医药
1.2458
自然村空间分布的数学模型:根据以上设定网格的方法,抽取了14个生境区,计算各区内自然村的mc、
 c、
c、 c/mc、s2
c/mc、s2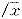 见表1。
见表1。由表1可见自然村的
 c/mc、s
c/mc、s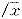 ,1、2区接近于1,其它区都小于1,基本达到了均匀分布。其空间分布动态模型为:
,1、2区接近于1,其它区都小于1,基本达到了均匀分布。其空间分布动态模型为: c=-0.2130+0.9267mc γ=0.9178,P=0.0001
c=-0.2130+0.9267mc γ=0.9178,P=0.0001, 百拇医药
其F=64.155,P=0.0001;tα=-1.112,P=0.2878;tβ=8.010,P=0.0001。
在0.05水平上回归方程及回归系数均有极显著性;B=0.0378,说明模型拟合极佳。因α=-0.2130,而P=0.2827>0.05,所以总体α为0,自然村分布的基本成分是单个个体;又β<0,所以自然村的空间格局是均匀分布。在此水平上研究HRFS的空间格局就消除了自然村的影响。
2.2 不同生境内的HRFS病例空间分布格局分析结果
由表1可见,HRFS的
 c/mc、s2
c/mc、s2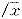 均大于1,说明其有明显的聚集性。进一步根据不同的生境特点做回归分析,其结果如下:
均大于1,说明其有明显的聚集性。进一步根据不同的生境特点做回归分析,其结果如下:, 百拇医药
① 将全县看作一个特定生境(共14个生境区):
空间格局模型:
 c=1.2476+2.0135mc,γ=0.7915,P=0.0007;
c=1.2476+2.0135mc,γ=0.7915,P=0.0007;模型检验:F=20.132,P=0.0007;tα=2.245,p=0.0444;tβ=4.487,p=0.0007;
模型精度:B=1.1000。
② 平原地带
生境特点:该区由3、4、5、6、7、11区组成,为平原,主要作物为小麦、玉米,境内的自然村一般较大。
, 百拇医药 空间格局模型:
 c=2.4466+1.3546mc,γ=0.8597,P=0.0281;
c=2.4466+1.3546mc,γ=0.8597,P=0.0281;模型检验:F=11.333,P=0.0281;tα=3.566,p=0.0235;tβ=3.366,p=0.0281;
模型精度:B=0.6467。
③ 山区干旱地带
生境特点:该区由1、8、9、10、12、13、14区组成,为山区干旱地带,主要作物地瓜、花生、以秋季作物为主。
空间格局模型:
 c=0.0605+3.0249mc,γ=0.9053,P=0.005;
c=0.0605+3.0249mc,γ=0.9053,P=0.005;, 百拇医药
模型检验:F=22.705,P=0.005;tα=0.133,p=0.9886;tβ=4.765,p=0.005;
模型精度:B=0.2240。
④ 涝洼、库区
生境特点:该区由2、3、4、5、7、8、11组成,其中2、3、4、5、7为平原区中涝洼较多的地带,8、11虽为山区、丘陵,但内有唐村、昌里两大水库位于其中。
空间格局模型:
 c=6.6753+3.3743mc+1.2273m2c,R2=0.9120;
c=6.6753+3.3743mc+1.2273m2c,R2=0.9120;, 百拇医药
模型检验:F=20.736,P=0.0077;tα=11.151,p=0.0004;tβ=4.160,p=0.0141;tγ=5.047,p=0.0072;
模型精度:B=0.0366。
由此可见,以全县为一大的生境时,α>0,HRFS病例的基本成分是群体,病例间存在某种流行病学联系;β>0,HRFS病例呈聚集分布。而按不同生境分别分析时,却各有特点:平原和涝洼、库区α值都较大,分别为2.4466、6.6753,病例间有较强的联系;它们的β的绝对值都大于1,分别为1.3546、3.3743,病例分布具有较高聚集性,且涝洼、库区的联系性和聚集性均大于平原。对于山区干旱地带,α为0.0605,P>0.05,所以病例的基本成分是个体,没有流行病学联系;而β为3.0249,表明病例的聚集性也较强。充分体现了HRFS在不同生境内的空间分布特点。关于
 c/mc和mc关系分布和疫点范围量化,限于篇幅将另文讨论。模型还可用于研究时间维上的某一特定生境内HRFS病例的空间分布动态规律,即对于某一特定生境,计算其内不同的时间HRFS病例分布的
c/mc和mc关系分布和疫点范围量化,限于篇幅将另文讨论。模型还可用于研究时间维上的某一特定生境内HRFS病例的空间分布动态规律,即对于某一特定生境,计算其内不同的时间HRFS病例分布的 c与mc,建立模型,以反映该特定生境内HRFS病例的空间分布随时间的变化规律。模型揭示对于平原和涝洼、库区在重点抓好病例聚集区内的灭鼠防病时,应注重发病“灶点”的处理;而对于平原干旱地带则不易采取“灶点”处理,而应当对整个病例聚集区采取措施。同时,提示我们对于HRFS的防治不能一刀切地搞“大面积灭鼠”,而必须因地制宜地根据其所处的生境特点采取相应的措施。■
c与mc,建立模型,以反映该特定生境内HRFS病例的空间分布随时间的变化规律。模型揭示对于平原和涝洼、库区在重点抓好病例聚集区内的灭鼠防病时,应注重发病“灶点”的处理;而对于平原干旱地带则不易采取“灶点”处理,而应当对整个病例聚集区采取措施。同时,提示我们对于HRFS的防治不能一刀切地搞“大面积灭鼠”,而必须因地制宜地根据其所处的生境特点采取相应的措施。■, http://www.100md.com
参考文献:
[1] Iwao,S and Kuno, E.Use of the regression of mean crowding on mean density for estimating sample size and the transformation of data for the analysis of variance. Res. Popul Ecol. 1984,210~214.
[2] Iwao, S. and Kuno, E:An approach to the analysis of aggregation patterns in biological populations. Statistical Ecology.1, 461~513,Penn State Univ. Press. 1971.
[3] Iwao,S: Application of the
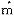 -m method to the analysis of spatial pattern by changing the quadrat sine. Res. Popul. Ecol. 1972,14(1):79~128.
-m method to the analysis of spatial pattern by changing the quadrat sine. Res. Popul. Ecol. 1972,14(1):79~128., http://www.100md.com
[4] 蔡晓明等.大白菜上七星瓢虫空间格局及抽样技术研究生态学杂志,1991,10(5):6~11.
[5] Iwao S. A new regression method for analysis the aggregation pattern of animal populations Res. Popul.Ecol. 1968,10(1):1~20.
[6] 徐汝梅等.改正的Iwao
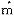 -m模型.生态学报,1984,4(2):111~118.
-m模型.生态学报,1984,4(2):111~118.[7] 胡良平.现代统计学与SAS应用.军事医学科学出版社,1996,215~265.
收稿日期:1999-03-09, 百拇医药