关于Weiss式中常量a求法的研究
作者：朱保恭
单位：朱保恭(西安医科大学生理教研室 西安710061)
关键词：
数理医药学杂志000112
中图分类号：R 444
文章编号：1004-4337(2000)01-0025-02▲
对组织兴奋性进行定量测定，是临床电诊断学上的重要方法之一。此外，在早产和慢性酒精中毒的诊断中对麻风病的电刺激疗法以及对心脏起博器的研制和应用上都有所应用。
以往曾有许多工作证明了Weiss式中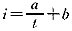
的常量a能正确反映兴奋性的高低。a是常量，但由于所用求a值的方法不同，在同一兴奋性条件下，又可得到不同的a值，这就使a的应用受到限制。为了更好地在实际中应用这一指标，我们对各种不同求a方法的可靠性通过实验数据进行了研究。
, 百拇医药
1 实验方法及资料
常规制备蛙离体坐骨神经标本，在双目解剖显微镜(Opton)下沿神经干纵轴将合适部位的被膜切开，以备插入微电极用，切口长约0.5～1.0cm，将标本移置浴槽中刺激电极上，用凡士林将刺激电极的正、负极隔开，浴槽中灌入适量任氏液，稳定30分钟后备用。
刺激电极用上海生理所产的垂直式微电极拉制仪拉成，其尖端直径小于0.5μ，阻抗20～40MΩ，其内充以3MKCI液，将直径约0.5mm的Ag-AgCl丝一端插入微电极尾部，另一端连于MEZ-8201微电极放大器探头，放大器输出端连于SBR-I二线示波器，用SEN-3201型刺激器产生方波脉冲，经SS-102J隔离器输出，频率为1次/2秒，刺激电极连于隔离器输出端。
用微电极推进器将微电极经被膜切口插入，同时观察MEZ-8201放大器显示的静息膜电位。调整微电极在神经干中位置，使膜电位值达-60mv左右，施加适当刺激则可见到具有超射的动作电位，常规测定i.t.c及tH。室温18℃～23℃。
, 百拇医药
表1 一般资料 实验材料
序号
Rp(mv)
Ap(mv)
Rh(mv)
tH(ms)
Chr(ms)
坐骨神经纤维
4
62
90
167
, 百拇医药 0.5
0.06
注：Rp为静息电位；Ap为动作电位；Rh为基强变；tH为主利用时；Chr为时值。
表2 强度-时间关系 序号
1
2
3
4
5
6
7
8
, 百拇医药
9
10
t(ms)
0.01
0.02
0.04
0.06
0.08
0.1
0.2
0.3
0.4
0.5
, 百拇医药
0.6
0.7
i(mv)
1190
695
412
325
278
253
200
179
171
167
, 百拇医药
167
167
it(mv*ms)
11.90
13.90
16.48
19.50
22.24
25.3
40.0
53.7
68.4
83.5
, 百拇医药
2 计算结果
2.1 Rh.Chr法
时值是两倍Rh条件下的t，按照传统看法，Rh=b，代入Weiss式后可得：
a=Rh.Chr=10.02
2.2 I.t法
由于Rh=b,设i-Rh=I,代入Weiss式后得：
a2=I.t=10.23
根据资料，t愈小，求得a愈精确，故选t=0.01的数值代入。
, 百拇医药
2.3 两点法
选t=0.04和t=0.02的两组数据带入Weiss式
解联立方程，得a3=11.03
2.4 平均法
理论上，同一组测量数据中出现正负偏差的机会应当相当，所以如将它们分为前后两组，各求出其平均值，然后按两点法计算，则可使解的精确程度提高：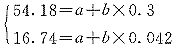
解得a4=10.65
2.5 直线回归法
, 百拇医药
Weiss式也可写成Q=a+bt，其中Q=it。故可按最小二乘法原理，用直线回归的方法求出，我们用casio fx-3600P计算器在“LR”状态下，进行直线回归，故得a5=10.72。
3 五种求a方法可靠程度的比较[1]
用5种不同的求a方法对同一实验例的数据进行计算，得到5个不同的a值。其中哪种方法最为可靠，可以通过各种方法计算结果的或然误差来判断。依据两种公式
di=Qi-Q′i
其中Qi为实测值，Q′i为根据公式求得的计算值，di为两值之偏差。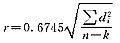
, http://www.100md.com
其中n为所测定的点数；k为Weiss式中常量数目；r为或然误差。
将∑d2i值及n=10,k=2代入上述第二个公式分别得到
Rh.Chr法：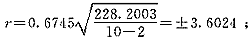
I.t法：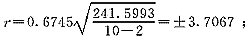
两点法：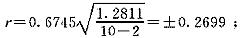
两组法：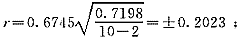
, 百拇医药
回归法：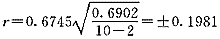
根据或然误差的意义，误差落在±范围内的应占50%，即
Rh.Chr法：误差落在±3.602之间的占50%；
I.t法：误差落在±3.707之间的占50%；
两点法：误差落在±0.270之间的占50%；
两组法：误差落在±0.202之间的占50%；
回归法：误差落在±0.198之间的占50%。
结果表明回归法和两组法最可靠，Rh.Chr法和I.t法最不可靠；与两组法相比，回归法似更可靠。在实际应用时应该用回归法求得a值。■
参考文献：
[1] 冯师颜.误差理论与实验理论处理.第一版.北京：科学出版社，1964，74～89.
收稿日期：1999-03-30, 百拇医药
单位：朱保恭(西安医科大学生理教研室 西安710061)
关键词：
数理医药学杂志000112
中图分类号：R 444
文章编号：1004-4337(2000)01-0025-02▲
对组织兴奋性进行定量测定，是临床电诊断学上的重要方法之一。此外，在早产和慢性酒精中毒的诊断中对麻风病的电刺激疗法以及对心脏起博器的研制和应用上都有所应用。
以往曾有许多工作证明了Weiss式中
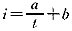的常量a能正确反映兴奋性的高低。a是常量，但由于所用求a值的方法不同，在同一兴奋性条件下，又可得到不同的a值，这就使a的应用受到限制。为了更好地在实际中应用这一指标，我们对各种不同求a方法的可靠性通过实验数据进行了研究。, 百拇医药
1 实验方法及资料
常规制备蛙离体坐骨神经标本，在双目解剖显微镜(Opton)下沿神经干纵轴将合适部位的被膜切开，以备插入微电极用，切口长约0.5～1.0cm，将标本移置浴槽中刺激电极上，用凡士林将刺激电极的正、负极隔开，浴槽中灌入适量任氏液，稳定30分钟后备用。
刺激电极用上海生理所产的垂直式微电极拉制仪拉成，其尖端直径小于0.5μ，阻抗20～40MΩ，其内充以3MKCI液，将直径约0.5mm的Ag-AgCl丝一端插入微电极尾部，另一端连于MEZ-8201微电极放大器探头，放大器输出端连于SBR-I二线示波器，用SEN-3201型刺激器产生方波脉冲，经SS-102J隔离器输出，频率为1次/2秒，刺激电极连于隔离器输出端。
用微电极推进器将微电极经被膜切口插入，同时观察MEZ-8201放大器显示的静息膜电位。调整微电极在神经干中位置，使膜电位值达-60mv左右，施加适当刺激则可见到具有超射的动作电位，常规测定i.t.c及tH。室温18℃～23℃。
, 百拇医药
表1 一般资料 实验材料
序号
Rp(mv)
Ap(mv)
Rh(mv)
tH(ms)
Chr(ms)
坐骨神经纤维
4
62
90
167
, 百拇医药 0.5
0.06
注：Rp为静息电位；Ap为动作电位；Rh为基强变；tH为主利用时；Chr为时值。
表2 强度-时间关系 序号
1
2
3
4
5
6
7
8
, 百拇医药
9
10
t(ms)
0.01
0.02
0.04
0.06
0.08
0.1
0.2
0.3
0.4
0.5
, 百拇医药
0.6
0.7
i(mv)
1190
695
412
325
278
253
200
179
171
167
, 百拇医药
167
167
it(mv*ms)
11.90
13.90
16.48
19.50
22.24
25.3
40.0
53.7
68.4
83.5
, 百拇医药
2 计算结果
2.1 Rh.Chr法
时值是两倍Rh条件下的t，按照传统看法，Rh=b，代入Weiss式后可得：
a=Rh.Chr=10.02
2.2 I.t法
由于Rh=b,设i-Rh=I,代入Weiss式后得：
a2=I.t=10.23
根据资料，t愈小，求得a愈精确，故选t=0.01的数值代入。
, 百拇医药
2.3 两点法
选t=0.04和t=0.02的两组数据带入Weiss式
解联立方程，得a3=11.03
2.4 平均法
理论上，同一组测量数据中出现正负偏差的机会应当相当，所以如将它们分为前后两组，各求出其平均值，然后按两点法计算，则可使解的精确程度提高：
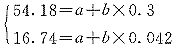
解得a4=10.65
2.5 直线回归法
, 百拇医药
Weiss式也可写成Q=a+bt，其中Q=it。故可按最小二乘法原理，用直线回归的方法求出，我们用casio fx-3600P计算器在“LR”状态下，进行直线回归，故得a5=10.72。
3 五种求a方法可靠程度的比较[1]
用5种不同的求a方法对同一实验例的数据进行计算，得到5个不同的a值。其中哪种方法最为可靠，可以通过各种方法计算结果的或然误差来判断。依据两种公式
di=Qi-Q′i
其中Qi为实测值，Q′i为根据公式求得的计算值，di为两值之偏差。
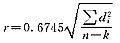
, http://www.100md.com
其中n为所测定的点数；k为Weiss式中常量数目；r为或然误差。
将∑d2i值及n=10,k=2代入上述第二个公式分别得到
Rh.Chr法：
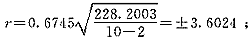
I.t法：
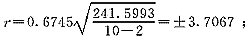
两点法：
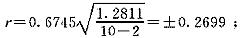
两组法：
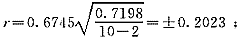
, 百拇医药
回归法：
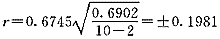
根据或然误差的意义，误差落在±范围内的应占50%，即
Rh.Chr法：误差落在±3.602之间的占50%；
I.t法：误差落在±3.707之间的占50%；
两点法：误差落在±0.270之间的占50%；
两组法：误差落在±0.202之间的占50%；
回归法：误差落在±0.198之间的占50%。
结果表明回归法和两组法最可靠，Rh.Chr法和I.t法最不可靠；与两组法相比，回归法似更可靠。在实际应用时应该用回归法求得a值。■
参考文献：
[1] 冯师颜.误差理论与实验理论处理.第一版.北京：科学出版社，1964，74～89.
收稿日期：1999-03-30, 百拇医药