模糊数学在评价疾病治疗质量中的应用
作者：王启栋 刘荣甫 王洁贞 陈常玲 鞠峰
单位：王启栋(济南军区总医院信息科 济南250031)； 刘荣甫(济南军区总医院信息科 济南250031)； 王洁贞(济南军区总医院信息科 济南250031 山东医科大学公共卫生学院)； 陈常玲(济南军区总医院信息科 济南250031)； 鞠峰(济南军区总医院信息科 济南250031)
关键词：模糊数学；综合评价；隶属度
数理医药学杂志000142
摘 要：以最大隶属度作为最终指标，对疾病的治疗质量进行综合评价，为医院管理决策提供了信息服务。
中图分类号：O 159
文章编号：1004-4337(2000)01-0073-02▲
, 百拇医药
模糊综合评价[1]是应用模糊数学的理论，将模糊信息通过模糊判断的手段，求得明确评价结果的一种综合评价方法。
在卫生事业管理工作中，有不少资料蕴藏的信息呈现模糊性，如医院管理质量的好坏，疾病治疗质量的好坏等等。当对这种资料进行分析评价时，需要采用模糊综合评价。由于被评价项目的各指标水平或等级间没有一个绝对明确的界限，可用模糊矩阵描述它们之间的关系，即用模糊矩阵对每个指标作模糊评价，再根据各指标对总体作用的大小确定相应的权重系数，通过权重系数和模糊评价矩阵的复合运算，得出一个较为清晰的归一化结论。
1 方法步骤
1.1 对一个评价系统给出一个指标集合以及评价集合
U={U1,U2……Un} U为指标集合
, 百拇医药
V={V1,V2……Vn} V为评价集合
1.2 建立U、V的模糊评价矩阵R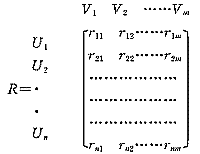
rij表示根据第i个指标对评价对象作出第j种评价的可能程度(隶属度)。
i=1,2…n j=1,2…m；且必须满足∑rij=1。
1.3 设置指标的权数分配A
简记为：A=(a1,a2,…an),且∑ai=1
, http://www.100md.com 1.4 矩阵合成
根据模糊矩阵乘法原理，将A与R合成，得到评价结果B。
B=A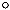
R=(b1,b2…bm)
这里“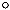”运算与普通矩阵乘法类似，区别在于把矩阵乘法中的“乘”换成取最小，“加”换成取最大[2]。
1.5 对B进行归一化处理
为方便比较，令∑b1=1,并设归一化处理的结果为模糊集合C，则
, 百拇医药 C=(b1/∑bi,b2/∑bi,…,bm/∑bi)
1.6 根据最大隶属度判断
取Ci最大数值所对应的评价等级为最后判定结果。
2 实例分析
我院1996、1997年脑出血治疗情况如表1所示，试对这两年的治疗质量进行综合评价。
表1 济南军区总医院1996、1997年脑出血治疗质量指标 年
份
例
, 百拇医药 数
疗 效(%)
平均
住院日
(天)
平均
费用
(元)
治愈率
好转率
未愈率
病死率
1996
, http://www.100md.com 59
32.20
49.15
3.39
15.26
29.08
6107.04
1997
49
36.73
53.06
0.00
10.21
, http://www.100md.com
23.37
6755.05
2.1 建立指标集合U及评价集合V
将治愈率、好转率、未愈率、病死率归为一类指标，即疗效。
指标集合：
U={疗效，平均住院日，平均费用}；
评价集合：
V={很好，好，一般，差}
2.2 建立U，V的模糊评价矩阵R
① 确定指标集合的评价等级标准(即U×V表)，见表2所示。表2 指标评价等级标准(U×V表) 指 标
, http://www.100md.com
评价等级
很好
好
一般
差
疗 效
治疗
好转
未愈
病死
平均住院日
≤20
21～25
, http://www.100md.com 26～30
>30
平均费用
≤3000
3001～5000
5001～6000
>6000
② 根据U×V表得两年资料的频数分配，见表3。表3 1996、1997年统计资料的频数分配 指 标
评价等级
很好
好
一般
, 百拇医药
差
疗 效
19，18
29，26
2，0
9，5
平均住院日
26，27
4，3
9，9
20，10
平均费用
21，14
, http://www.100md.com
15，13
1，5
22，17
③根据统计资料的频数分配建立模糊矩阵。
2.3 分配指标的权重如下： 疗效
平均住院日
平均费用
0.60
0.25
0.15
得权数集合A=(0.60,0.25,0.15)
, 百拇医药
2.4 将A与R合成，得评价结果B[2]。
B=A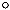R，于是
∑bi=1.21
∑bi=1.29
2.5 对B进行归一化处理得到C
C96=(0.32/1.21,0.49/1.21,0.15/1.21,0.25/1.21)
, 百拇医药
=(0.26,0.41,0.12,0.21)
C97=(0.37/1.29,0.53/1.29,0.18/1.29,0.21/1.29)
=(0.29,0.41,0.14,0.16)
2.6 综合评价
根据隶属度进行疾病治疗质量的综合评价。以两年最大隶属度(Cj)来判断疾病的治疗质量，本例1996年为0.41，1997年也为0.41，均属于等级“好”这一等级，结合“很好”这一等级的隶属度分析，分别将两个等级的隶属度相加，1996年为0.67，1997年为0.70。因此可以认为1997年脑出血的治疗质量比1996年有所提高。■
参考文献：
[1] 宇传华主编.卫生管理统计.西安：第四军医大学出版社，1994，122～126.
[2] 高慕勤主编.卫生管理运筹学.上海：第二军医大学出版社，1995，161～164.
收稿日期：1999-05-04, 百拇医药
单位：王启栋(济南军区总医院信息科 济南250031)； 刘荣甫(济南军区总医院信息科 济南250031)； 王洁贞(济南军区总医院信息科 济南250031 山东医科大学公共卫生学院)； 陈常玲(济南军区总医院信息科 济南250031)； 鞠峰(济南军区总医院信息科 济南250031)
关键词：模糊数学；综合评价；隶属度
数理医药学杂志000142
摘 要：以最大隶属度作为最终指标，对疾病的治疗质量进行综合评价，为医院管理决策提供了信息服务。
中图分类号：O 159
文章编号：1004-4337(2000)01-0073-02▲
, 百拇医药
模糊综合评价[1]是应用模糊数学的理论，将模糊信息通过模糊判断的手段，求得明确评价结果的一种综合评价方法。
在卫生事业管理工作中，有不少资料蕴藏的信息呈现模糊性，如医院管理质量的好坏，疾病治疗质量的好坏等等。当对这种资料进行分析评价时，需要采用模糊综合评价。由于被评价项目的各指标水平或等级间没有一个绝对明确的界限，可用模糊矩阵描述它们之间的关系，即用模糊矩阵对每个指标作模糊评价，再根据各指标对总体作用的大小确定相应的权重系数，通过权重系数和模糊评价矩阵的复合运算，得出一个较为清晰的归一化结论。
1 方法步骤
1.1 对一个评价系统给出一个指标集合以及评价集合
U={U1,U2……Un} U为指标集合
, 百拇医药
V={V1,V2……Vn} V为评价集合
1.2 建立U、V的模糊评价矩阵R
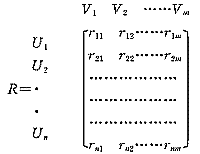
rij表示根据第i个指标对评价对象作出第j种评价的可能程度(隶属度)。
i=1,2…n j=1,2…m；且必须满足∑rij=1。
1.3 设置指标的权数分配A
简记为：A=(a1,a2,…an),且∑ai=1
, http://www.100md.com 1.4 矩阵合成
根据模糊矩阵乘法原理，将A与R合成，得到评价结果B。
B=A
R=(b1,b2…bm)这里“
”运算与普通矩阵乘法类似，区别在于把矩阵乘法中的“乘”换成取最小，“加”换成取最大[2]。1.5 对B进行归一化处理
为方便比较，令∑b1=1,并设归一化处理的结果为模糊集合C，则
, 百拇医药 C=(b1/∑bi,b2/∑bi,…,bm/∑bi)
1.6 根据最大隶属度判断
取Ci最大数值所对应的评价等级为最后判定结果。
2 实例分析
我院1996、1997年脑出血治疗情况如表1所示，试对这两年的治疗质量进行综合评价。
表1 济南军区总医院1996、1997年脑出血治疗质量指标 年
份
例
, 百拇医药 数
疗 效(%)
平均
住院日
(天)
平均
费用
(元)
治愈率
好转率
未愈率
病死率
1996
, http://www.100md.com 59
32.20
49.15
3.39
15.26
29.08
6107.04
1997
49
36.73
53.06
0.00
10.21
, http://www.100md.com
23.37
6755.05
2.1 建立指标集合U及评价集合V
将治愈率、好转率、未愈率、病死率归为一类指标，即疗效。
指标集合：
U={疗效，平均住院日，平均费用}；
评价集合：
V={很好，好，一般，差}
2.2 建立U，V的模糊评价矩阵R
① 确定指标集合的评价等级标准(即U×V表)，见表2所示。表2 指标评价等级标准(U×V表) 指 标
, http://www.100md.com
评价等级
很好
好
一般
差
疗 效
治疗
好转
未愈
病死
平均住院日
≤20
21～25
, http://www.100md.com 26～30
>30
平均费用
≤3000
3001～5000
5001～6000
>6000
② 根据U×V表得两年资料的频数分配，见表3。表3 1996、1997年统计资料的频数分配 指 标
评价等级
很好
好
一般
, 百拇医药
差
疗 效
19，18
29，26
2，0
9，5
平均住院日
26，27
4，3
9，9
20，10
平均费用
21，14
, http://www.100md.com
15，13
1，5
22，17
③根据统计资料的频数分配建立模糊矩阵。
2.3 分配指标的权重如下： 疗效
平均住院日
平均费用
0.60
0.25
0.15
得权数集合A=(0.60,0.25,0.15)
, 百拇医药
2.4 将A与R合成，得评价结果B[2]。
B=A
R，于是∑bi=1.21
∑bi=1.29
2.5 对B进行归一化处理得到C
C96=(0.32/1.21,0.49/1.21,0.15/1.21,0.25/1.21)
, 百拇医药
=(0.26,0.41,0.12,0.21)
C97=(0.37/1.29,0.53/1.29,0.18/1.29,0.21/1.29)
=(0.29,0.41,0.14,0.16)
2.6 综合评价
根据隶属度进行疾病治疗质量的综合评价。以两年最大隶属度(Cj)来判断疾病的治疗质量，本例1996年为0.41，1997年也为0.41，均属于等级“好”这一等级，结合“很好”这一等级的隶属度分析，分别将两个等级的隶属度相加，1996年为0.67，1997年为0.70。因此可以认为1997年脑出血的治疗质量比1996年有所提高。■
参考文献：
[1] 宇传华主编.卫生管理统计.西安：第四军医大学出版社，1994，122～126.
[2] 高慕勤主编.卫生管理运筹学.上海：第二军医大学出版社，1995，161～164.
收稿日期：1999-05-04, 百拇医药