引入协变量比较药物的效果
作者:娄冬华
单位:娄冬华(南京医科大学卫生统计教研室 南京210029)
关键词:协变量;协方差分析
数理医药学杂志000138
摘 要:在比较多个处理前后或多组样本同一个处理前后某指标观察值变化的显著性作方差分析时,处理前几组观察值应无显著差异,如果处理前有差异可将处理前的观察值作为协变量作协方差分析。
中图分类号:O 212.4
文章编号:1004-4337(2000)01-0066-02▲
几种不同处理的效应的比较当响应值满足正态分布和方差齐性条件时,可以应用t检验或方差分析去处理,但是要求除了要比较的因素不同之外,其它对结果有影响的非处理因素要做到均衡性,否则方差分析的结果中就掺杂了非处理因素的效应。这种均衡性应在设计阶段中完成,但有时事先未充分考虑到,或其本身无法控制时,可以引入协变量去处理。
, http://www.100md.com
1 模型与分析
单因子一个协变量的协方差分析模型是:Yij=μ+αi+γXij+εij i=1,…k,j=1,…,ni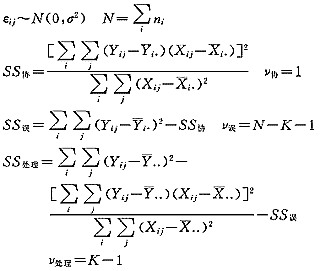
均方和 MS=SS/ν
F协=MS协/MS误 F处=MS处/MS误
其中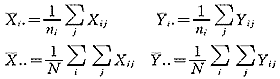
例 心脏与脑血管梗塞是引起人类死亡的主要原因之一,它们与高血压有着密切的联系。现在作一次研究,对一些病人发送一种抗高血压药品,实验对象按年龄和社会经济方面的特征分为两组,实验数据如表1。
, 百拇医药
表1 两组人群用药前后舒张压(mmHg) A组
B组
前X1j
后Z1j
差Y1j
前X2j
后Z2j
差Y2j
102
82
26
, http://www.100md.com
92
78
14
108
100
8
98
88
10
102
86
16
100
88
, 百拇医药
12
118
88
30
100
82
18
120
100
20
95
76
19
120
, 百拇医药
100
20
88
88
0
105
92
13
90
76
14
108
88
20
, 百拇医药
98
82
16
108
90
18
90
74
16
106
94
12
98
86
, 百拇医药
12
102
86
16
98
86
12
110
84
26
104
92
12
105
, 百拇医药
82
23
102
84
18
104
86
18
105
85
20
106
88
18
, 百拇医药
人们常用的方法是对两组血压的变化置Yij作t检验或方差分析,方差分析的结果见表2。表2 血压变化量的方差分析 来源
平方和
自由度
均方和
F
P
处理
232.40
1
232.40
8.34
0.0076
, http://www.100md.com
误差
752.77
27
27.88
总
985.17
28
结果为差别显著,但是这两组人用药前的血压是否相同呢?我们可以作两组用药前血压的方差分析,结果见表3。表3 用药前两组血压的方差分析 来源
平方和
自由度
均方和
F
, http://www.100md.com
P
处理
1041.95
1
1041.95
34.69
0.0001
误差
811.01
27
30.04
总
1852.96
, 百拇医药
28
表3说明两组人群在用药前舒张压之间差异显著,那么导致血压变化量的差异的原因有二:一是该药对两组人群的效果不同;二是两组人群用药前血压不同(可能该药对血压较高的病人效果较好)。此时,可以将用药前血压值作为一个协变量,建立协方差分析模型,计算结果见表4。表4 两组人群血压变化的协方差分析 来源
平方和
自由度
均方和
F
P
协变量
118.08
1
, http://www.100md.com
118.08
4.84
0.0369
处理
3.75
1
3.75
0.15
0.6982
误差
634.69
26
24.41
, http://www.100md.com
如果将用药前两组人的血压值作为协变量,即消除了两组人用药前不同的影响后,两组人的效应无差别,与不消除影响结论相反。
2 讨论
对于多组比较及多因子、多个协变量的情况,同样可以处理,是否需要引入协变量视具体情况而定。如果在处理前几组观察值已经做到均衡性或其对观察结果影响不大时,可以不引入协变量,用方差分析处理,否则宜将处理前的观察值作为协变量,作协方差分析。■
参考文献:
[1] 王松桂.线性模型的理论及其应用.安徽教育出版社,1987.
[2] SAS/STAT Users Guide, Version 6, Fourth Edition Volume 2, Cary, USA, 1994.
收稿日期:1999-03-21, http://www.100md.com
单位:娄冬华(南京医科大学卫生统计教研室 南京210029)
关键词:协变量;协方差分析
数理医药学杂志000138
摘 要:在比较多个处理前后或多组样本同一个处理前后某指标观察值变化的显著性作方差分析时,处理前几组观察值应无显著差异,如果处理前有差异可将处理前的观察值作为协变量作协方差分析。
中图分类号:O 212.4
文章编号:1004-4337(2000)01-0066-02▲
几种不同处理的效应的比较当响应值满足正态分布和方差齐性条件时,可以应用t检验或方差分析去处理,但是要求除了要比较的因素不同之外,其它对结果有影响的非处理因素要做到均衡性,否则方差分析的结果中就掺杂了非处理因素的效应。这种均衡性应在设计阶段中完成,但有时事先未充分考虑到,或其本身无法控制时,可以引入协变量去处理。
, http://www.100md.com
1 模型与分析
单因子一个协变量的协方差分析模型是:Yij=μ+αi+γXij+εij i=1,…k,j=1,…,ni
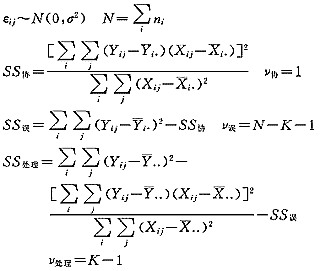
均方和 MS=SS/ν
F协=MS协/MS误 F处=MS处/MS误
其中
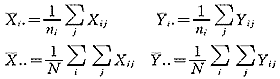
例 心脏与脑血管梗塞是引起人类死亡的主要原因之一,它们与高血压有着密切的联系。现在作一次研究,对一些病人发送一种抗高血压药品,实验对象按年龄和社会经济方面的特征分为两组,实验数据如表1。
, 百拇医药
表1 两组人群用药前后舒张压(mmHg) A组
B组
前X1j
后Z1j
差Y1j
前X2j
后Z2j
差Y2j
102
82
26
, http://www.100md.com
92
78
14
108
100
8
98
88
10
102
86
16
100
88
, 百拇医药
12
118
88
30
100
82
18
120
100
20
95
76
19
120
, 百拇医药
100
20
88
88
0
105
92
13
90
76
14
108
88
20
, 百拇医药
98
82
16
108
90
18
90
74
16
106
94
12
98
86
, 百拇医药
12
102
86
16
98
86
12
110
84
26
104
92
12
105
, 百拇医药
82
23
102
84
18
104
86
18
105
85
20
106
88
18
, 百拇医药
人们常用的方法是对两组血压的变化置Yij作t检验或方差分析,方差分析的结果见表2。表2 血压变化量的方差分析 来源
平方和
自由度
均方和
F
P
处理
232.40
1
232.40
8.34
0.0076
, http://www.100md.com
误差
752.77
27
27.88
总
985.17
28
结果为差别显著,但是这两组人用药前的血压是否相同呢?我们可以作两组用药前血压的方差分析,结果见表3。表3 用药前两组血压的方差分析 来源
平方和
自由度
均方和
F
, http://www.100md.com
P
处理
1041.95
1
1041.95
34.69
0.0001
误差
811.01
27
30.04
总
1852.96
, 百拇医药
28
表3说明两组人群在用药前舒张压之间差异显著,那么导致血压变化量的差异的原因有二:一是该药对两组人群的效果不同;二是两组人群用药前血压不同(可能该药对血压较高的病人效果较好)。此时,可以将用药前血压值作为一个协变量,建立协方差分析模型,计算结果见表4。表4 两组人群血压变化的协方差分析 来源
平方和
自由度
均方和
F
P
协变量
118.08
1
, http://www.100md.com
118.08
4.84
0.0369
处理
3.75
1
3.75
0.15
0.6982
误差
634.69
26
24.41
, http://www.100md.com
如果将用药前两组人的血压值作为协变量,即消除了两组人用药前不同的影响后,两组人的效应无差别,与不消除影响结论相反。
2 讨论
对于多组比较及多因子、多个协变量的情况,同样可以处理,是否需要引入协变量视具体情况而定。如果在处理前几组观察值已经做到均衡性或其对观察结果影响不大时,可以不引入协变量,用方差分析处理,否则宜将处理前的观察值作为协变量,作协方差分析。■
参考文献:
[1] 王松桂.线性模型的理论及其应用.安徽教育出版社,1987.
[2] SAS/STAT Users Guide, Version 6, Fourth Edition Volume 2, Cary, USA, 1994.
收稿日期:1999-03-21, http://www.100md.com