作者:ZHAO Guolong(Henan Medical University Zhengzhou 450052) Heidi Holmes Morgan(University of Kansas Medical Center Kansas 66160)
单位:
关键词:Censorship;Effective sample size;Rate test;Sample size
数理医药学杂志000353A NONPARAMETRIC PROCEDURE OF THE SAMPLE
SIZE DETERMINATION FOR SURVIVAL RATE TEST
ZHAO Guolong
(Henan Medical University Zhengzhou 450052)
Heidi Holmes Morgan
(University of Kansas Medical Center Kansas 66160)
Abstract Objective This paper proposes a nonparametric procedure of the sample size determination for survival rate test. Methods Using the classical asymptotic normal procedure yields the required homogenetic effective sample size and using the inverse operation with the prespecified value of the survival function of censoring times yields the required sample size. Results It is matched with the rate test for censored data, does not involve survival distributions, and reduces to its classical counterpart when there is no censoring. The observed power of the test coincides with the prescribed power under usual clinical conditions. Conclusion It can be used for planning survival studies of chronic diseases.
Key works Censorship Effective sample size Rate test Sample size
中图分类号:O 213.9 文献标识码:A
文章编号:1004-4337(2000)03-0273-05
In the survival studies of chronic diseases, the most frequently used methods of data analysis are the nonparametric estimations and comparisons of survival rates at different times but there have been no matched methods for determining the required sample size so far. Instead have been often used the parametric methods based on the assumption of exponential distributions[1~7] such that the relevant sample sizes may not be satisfied with the prescribed power.
This paper reports a nonparametric procedure of the sample size determination for survival rate test.
1 Survival Rate Test
Let Xi(i=1,…,n) be independent and identically distributed (i.i.d.) failure times of individuals with continuous distribution function Fx(t)=Pr(Xi≤t). Its complement is survival function Sx(t)=1-Fx(t). Let Ci be i.i.d. censoring times with distribution function Fc(t)=Pr(Ci(t). The corresponding survival function is Sc(t)=1-Fc(t). Suppose C is independent of X so that Fc is functionally independent of Fx. Suppose we observe a sequence of paires (Ti,δi)(i=1,…,n) such that Ti=min(Xi,Ci) Where δi=1 if Xi≤Ci and δi=0 if Xi>Ci. Permutation gives order statistics T(1)<…(n) and the corresponding indicator δ(1),…,δ(n).
The Kaplan-Meier estimate[8] for Sx(t) is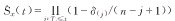 (1) (1)
Its homogenetic effective sample size is given by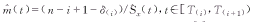 (2) (2)
It declines with the censoring vector (1-δ(i))[9]: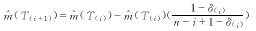 (3) (3)
and reduces to the sample size when there is no censoring: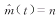
Let π be the expectation of 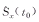 at some interested time t0 with π=π0 under a null hypothesis H0 and π=π1 under an alternative hypothesis H1, where π1≠π0 (two sided test) or π1>π0 or π1<π0(one sided). By the asymptotic normality of Kaplan-Meier estimate[10], the statistic for festing H0 is at some interested time t0 with π=π0 under a null hypothesis H0 and π=π1 under an alternative hypothesis H1, where π1≠π0 (two sided test) or π1>π0 or π1<π0(one sided). By the asymptotic normality of Kaplan-Meier estimate[10], the statistic for festing H0 is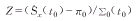 (4) (4)
where 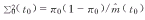 . Thus, we have Z~N(0,1) if H0 is true. By contrast with its classical counterpart[11], the only change is that the sample size n is replaced by the observed homogenetic effective sample size . Thus, we have Z~N(0,1) if H0 is true. By contrast with its classical counterpart[11], the only change is that the sample size n is replaced by the observed homogenetic effective sample size 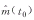 in (4). in (4).
2 Determination of Required Sample Size
The determination of required homogenetic effective sample size can inherit the classical asymptotic normal procedure[12]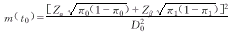 (5) (5)
where Zα and Zβ are the standard normal deviates at levels α and β the essential design parameters respectively and D0=π1-π0 is the selected maximum error, ie. the principle design parameter.
As for the required sample size, it can be realized by the inverse operation from m(t0) to n. Then it is useful to estimate the survival function of censoring times (6) (6)
It follows that 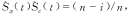 ...... ......
|