Hopfield型连续神经网络模型的稳定性
作者：樊爱军 朱志富 余小平
单位：樊爱军(第三军医大学基础部数学教研室 重庆400038)；朱志富(重庆通讯学院教研部)；余小平(第三军医大学营养卫生学教研室)
关键词：神经网络；正平衡态；全局渐近稳定
数理医药学杂志000305
摘 要 利用单调流方法得到一类Hopfield型连续神经网络模型存在唯一全局渐近稳定正平衡态的充分条件。
中图分类号：Q-332 文献标识码：A
文章编号：1004-4337(2000)03-0200-02
Hophield型连续神经网络模型[1]在最优化计算和联想记忆等方面已有重要的应用。神经网络应用于最优化计算(如求二次型多元函数的最值点)时，理想的情形是能够将此最优化问题映射成一个连续反馈神经网络，使它具有对应于目标函数最值点的唯一全局平衡态吸引子，且从相空间中任一点出发的网络运动轨道都将趋于该平衡态吸引子，这即是相当于要设计出具有全局稳定平衡态吸引子的连续反馈神经网络。1993年，在取消突触强度矩阵对称的假设下，廖晓昕[2]给出了Hopfield型连续神经网络平衡态稳定性的一系列判别准则，讨论了模型平衡态的存在唯一性。本文在不同于文献[2]的假设下，重新得到了模型存在全局渐近稳定正平衡态的充分条件。
, http://www.100md.com
1 模型及主要结论
本文讨论由美国生物物理学家Hopfield在80年代提出的连续神经网络模型：
(1)
其中，ui,Ci,Ri分别为电压、电容和电阻；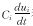
表示输入电流向人工神经元i的电容充电至电位ui的电流；Tijfj(uj)表示神经网络中人工神经元j输出端电压通过神经元间连接电导Tij产生的电流，Tij是神经元j、i之间的突触传递强度；fi表示神经元j的模式函数，因此
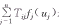是所有与神经元i相连接的神经元对神经元i提供的电流；
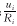表示i神经元因存在膜电阻而产生的漏电流；Ii表示从神经网络外部流入本人工神经网络的电流。一般假设模式函数fj连续、有界单调增且fj(0)=0，即存在正常数αj、βj,j=1,2,…,n，使|fj|≤αj,0j≤βj。
, 百拇医药
对模型(1)，本文始终作如下假设：
Tij≥0,i≠j,Ii>0 (2)
在假设(2)之下，我们讨论了系统(1)的流的性质、平衡态的存在唯一性及其稳定性等问题，得到了如下的本文主要定理：
定理1 如果矩阵A稳定，那么系统(1)存在唯一全局渐近稳定的正平衡态U*=(u*1,u*2,…,u*n),使得对任意初值U0∈Rn,当t→+∞时，其解都有φt(U0)→U*。其中，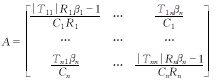
, 百拇医药
2 结论的证明
我们首先证明如下引理：
引理1 在假设(2)下，系统(1)的流单调。
证明：记
这里U=(u1,u2,…,un)T，则有
由Kamke定量[3]即可得结果U1≤U2(U12),那么对t≥0，系统(1)的流满足φt(U1)≤φt(U2)(φt(U1)<φt(U2)),即系统(1)的流单调。
, 百拇医药
引理2 系统(1)的所有解有界。
证明：对系统(1)的任意解U(t)=(u1(t),u2(t),…,un(t))T,令
Vi=u2i(t), i=1,2,…,n
则有
其中，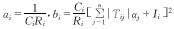
，所以
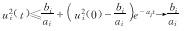
由U(t)的任意性，即可得系统(1)的所有解有界。
, http://www.100md.com
引理3 如果矩阵A稳定，那么系统(1)存在唯一的正平衡态U*。
证明：因为
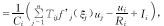
这里ξj为0和uj之间的某数。利用fj的有界性，所以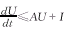
其中A如定理1所述，
。由于矩阵A稳定，I>0，利用文献[4]中定理1.1，1.2便可得系统(1)的正平衡态U*存在。
, http://www.100md.com
如果系统(1)存在两个平衡态U*,V*且U*≠V*，那么因为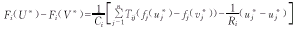
这里ηj为u*j和v*j之间的某数，所以
0=F(U*)-F(V*)=B(U*-V*)，其中，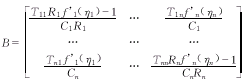
显然有B≤A,所以矩阵B稳定，故不可约。由Crammev规则必有U*-V*=0，矛盾。
, 百拇医药
所以系统(1)存在唯一正平衡态。
参考文献
1，Hopfield JJ. Neural networks and physics systems with emergent collective computertation abilities. Proc Natl Acad Sci USA, 1982,79:2554～2558.
2，廖晓昕.Hopfield型神经网络的稳定性.中国科学(A辑).1993，23：1025～1035.
3，Hirsch MW. Systems of differential equations that are competitive or cooperative Ⅱ：convergence almost everywhere. SIAMJ Math Anal. 1985,16:423～439.
4，Smith HL. On the asymptotic behavior of a class of deterministic models of cooperative species. SIAM J Appl Math. 1986,46:368～375.
5，Hirsch MW. The dynamical systems approach to differential equations. Bull Amer Math Soc. 1984,11:1～64.
收稿日期：1999-11-05, http://www.100md.com
单位：樊爱军(第三军医大学基础部数学教研室 重庆400038)；朱志富(重庆通讯学院教研部)；余小平(第三军医大学营养卫生学教研室)
关键词：神经网络；正平衡态；全局渐近稳定
数理医药学杂志000305
摘 要 利用单调流方法得到一类Hopfield型连续神经网络模型存在唯一全局渐近稳定正平衡态的充分条件。
中图分类号：Q-332 文献标识码：A
文章编号：1004-4337(2000)03-0200-02
Hophield型连续神经网络模型[1]在最优化计算和联想记忆等方面已有重要的应用。神经网络应用于最优化计算(如求二次型多元函数的最值点)时，理想的情形是能够将此最优化问题映射成一个连续反馈神经网络，使它具有对应于目标函数最值点的唯一全局平衡态吸引子，且从相空间中任一点出发的网络运动轨道都将趋于该平衡态吸引子，这即是相当于要设计出具有全局稳定平衡态吸引子的连续反馈神经网络。1993年，在取消突触强度矩阵对称的假设下，廖晓昕[2]给出了Hopfield型连续神经网络平衡态稳定性的一系列判别准则，讨论了模型平衡态的存在唯一性。本文在不同于文献[2]的假设下，重新得到了模型存在全局渐近稳定正平衡态的充分条件。
, http://www.100md.com
1 模型及主要结论
本文讨论由美国生物物理学家Hopfield在80年代提出的连续神经网络模型：
(1)其中，ui,Ci,Ri分别为电压、电容和电阻；
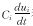表示输入电流向人工神经元i的电容充电至电位ui的电流；Tijfj(uj)表示神经网络中人工神经元j输出端电压通过神经元间连接电导Tij产生的电流，Tij是神经元j、i之间的突触传递强度；fi表示神经元j的模式函数，因此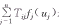是所有与神经元i相连接的神经元对神经元i提供的电流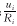；表示i神经元因存在膜电阻而产生的漏电流；Ii表示从神经网络外部流入本人工神经网络的电流。一般假设模式函数fj连续、有界单调增且fj(0)=0，即存在正常数αj、βj,j=1,2,…,n，使|fj|≤αj,0, 百拇医药
对模型(1)，本文始终作如下假设：
Tij≥0,i≠j,Ii>0 (2)
在假设(2)之下，我们讨论了系统(1)的流的性质、平衡态的存在唯一性及其稳定性等问题，得到了如下的本文主要定理：
定理1 如果矩阵A稳定，那么系统(1)存在唯一全局渐近稳定的正平衡态U*=(u*1,u*2,…,u*n),使得对任意初值U0∈Rn,当t→+∞时，其解都有φt(U0)→U*。其中，
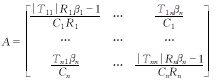
, 百拇医药
2 结论的证明
我们首先证明如下引理：
引理1 在假设(2)下，系统(1)的流单调。
证明：记
这里U=(u1,u2,…,un)T，则有
由Kamke定量[3]即可得结果U1≤U2(U1
, 百拇医药
引理2 系统(1)的所有解有界。
证明：对系统(1)的任意解U(t)=(u1(t),u2(t),…,un(t))T,令
Vi=u2i(t), i=1,2,…,n
则有
其中，
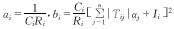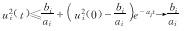
，所以由U(t)的任意性，即可得系统(1)的所有解有界。
, http://www.100md.com
引理3 如果矩阵A稳定，那么系统(1)存在唯一的正平衡态U*。
证明：因为
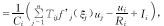
这里ξj为0和uj之间的某数。利用fj的有界性，所以
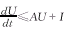
其中A如定理1所述，
。由于矩阵A稳定，I>0，利用文献[4]中定理1.1，1.2便可得系统(1)的正平衡态U*存在。, http://www.100md.com
如果系统(1)存在两个平衡态U*,V*且U*≠V*，那么因为
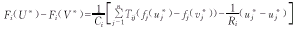
这里ηj为u*j和v*j之间的某数，所以
0=F(U*)-F(V*)=B(U*-V*)，其中，
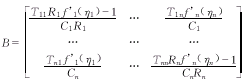
显然有B≤A,所以矩阵B稳定，故不可约。由Crammev规则必有U*-V*=0，矛盾。
, 百拇医药
所以系统(1)存在唯一正平衡态。
参考文献
1，Hopfield JJ. Neural networks and physics systems with emergent collective computertation abilities. Proc Natl Acad Sci USA, 1982,79:2554～2558.
2，廖晓昕.Hopfield型神经网络的稳定性.中国科学(A辑).1993，23：1025～1035.
3，Hirsch MW. Systems of differential equations that are competitive or cooperative Ⅱ：convergence almost everywhere. SIAMJ Math Anal. 1985,16:423～439.
4，Smith HL. On the asymptotic behavior of a class of deterministic models of cooperative species. SIAM J Appl Math. 1986,46:368～375.
5，Hirsch MW. The dynamical systems approach to differential equations. Bull Amer Math Soc. 1984,11:1～64.
收稿日期：1999-11-05, http://www.100md.com