Poisson分布资料的治疗前后比较检验方法
作者：赵耐青
单位：赵耐青(上海医科大学数学教研室 上海200032)
关键词：
数理医药学杂志000523
中图分类号： O 211.9 文献标识码： B 文章编号：1004-4337(2000)05-0424-02
在临床医学上，常有一类疾病是不易根治的(如支气管哮喘、癫痫等疾病)，在临床上常采取药物控制治疗，使患者不发作或少发作这类疾病。因此在临床研究中常需要通过考察治疗前后的患者发病次数对某个治疗方案的疗效进行评判。在某一个固定时期，一个患者的发病次数是随机的，可以认为近似服从Poisson分布。因此考察某控制治疗方案是否有效的问题就是考察患者治疗前后的发病次数是否减少，由于治疗后的发病情况与治疗前发病情况有关，故不能采用两组Poisson资料均数比较的统计方法进行检验。目前尚无有关文献报道此类资料的统计方法，所以本文将导出这类资料的统计检验方法。
, http://www.100md.com
1 方法
设第i个病例在治疗前的一个时期[-T,0]中的发病次数为Xi,且记λix=E(Xi)=exp(αi)，该病例在治疗后的一个时期[0,T]中的发病次数为Yi，并假定治疗后的患者发病次数与仅与治疗前的总体平均发病次数有关，则记λiy=E(Yi|Xi)=exp(αi+β)，因此治疗前后是否有变化的充要条件为β≠0。记(xi,yi)为(Xi,Yi)的样本点，(Xi,Yi)的联合概率密度为
,则似然函数为：
, 百拇医药
对数似然函数为：
由
解得：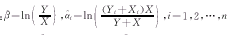
其中
所以当H0∶β=0成立时，对应检验统计量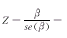
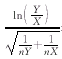近似服从N(0，1)分布，因此检验治疗前后发病次数是否发生改变的问题也就是应用上述检验方法进行检验。
, http://www.100md.com
2 实例应用
例 某医院为了评价某治疗方案是否能有效控制4～5岁儿童癫痫发病情况，在考虑和控制有关混杂因素后，随机收治了20名患有癫痫的儿童，其治疗前一年和治疗后一年的发病情况如下： 患者编号
1
2
3
4
5
6
7
8
9
, 百拇医药 10
11
12
13
14
15
16
17
18
19
20
治疗前发病次数
6
11
, 百拇医药
12
10
8
4
8
10
12
12
5
12
10
8
8
9
, 百拇医药
15
10
7
9
治疗后发病次数
8
10
7
8
9
5
7
10
7
, 百拇医药
5
4
7
10
7
7
5
9
7
9
8
治疗前平均发病次数
, 百拇医药 治疗后平均发病次数
1-0.8018=19.892%，因此治疗后的发病次数与治疗前发病次数相比，下降了19.892%。
。因为|Z|>1.96，对应的P<0.05，所以拒绝无效假设H0∶β=0，因此可以认为治疗后癫痫发病次数比治疗前有显著下降(控制癫痫发作的疗效是显著的)。3 讨论
本文给出Poisson分布资料前后对照的检验方法和例子，eβ是治疗后发病次数的总体均数与治疗前发病次数的总体均数之比。在实际应用时，应注意混杂因素对结果的影响，特别如年龄等混杂因素的影响。在可能的情况下，应采用随机对照试验(Random Control Trial, RCT)设计进行疗效评价研究，并通过随机分组平衡可能的混杂因素影响。由于篇幅所限，对于RCT设计的疗效评价研究中Poisson分布资料，作者只能在另文中论述。
参 考 文 献
1，Dobson AJ, An Introduction to Generalized Linear Models, Printed in Great Britain by T. J. Press(Padstow) Ltd, Padstow, Gornwall in 1991.
2，金丕焕.医用统计方法.上海医科大学出版社，1992.
收稿日期：2000-01-21, 百拇医药
单位：赵耐青(上海医科大学数学教研室 上海200032)
关键词：
数理医药学杂志000523
中图分类号： O 211.9 文献标识码： B 文章编号：1004-4337(2000)05-0424-02
在临床医学上，常有一类疾病是不易根治的(如支气管哮喘、癫痫等疾病)，在临床上常采取药物控制治疗，使患者不发作或少发作这类疾病。因此在临床研究中常需要通过考察治疗前后的患者发病次数对某个治疗方案的疗效进行评判。在某一个固定时期，一个患者的发病次数是随机的，可以认为近似服从Poisson分布。因此考察某控制治疗方案是否有效的问题就是考察患者治疗前后的发病次数是否减少，由于治疗后的发病情况与治疗前发病情况有关，故不能采用两组Poisson资料均数比较的统计方法进行检验。目前尚无有关文献报道此类资料的统计方法，所以本文将导出这类资料的统计检验方法。
, http://www.100md.com
1 方法
设第i个病例在治疗前的一个时期[-T,0]中的发病次数为Xi,且记λix=E(Xi)=exp(αi)，该病例在治疗后的一个时期[0,T]中的发病次数为Yi，并假定治疗后的患者发病次数与仅与治疗前的总体平均发病次数有关，则记λiy=E(Yi|Xi)=exp(αi+β)，因此治疗前后是否有变化的充要条件为β≠0。记(xi,yi)为(Xi,Yi)的样本点，(Xi,Yi)的联合概率密度为
,则似然函数为：, 百拇医药
对数似然函数为：
由
解得：
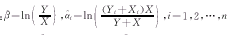
其中
所以当H0∶β=0成立时，对应检验统计量
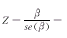
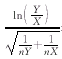近似服从N(0，1)分布，因此检验治疗前后发病次数是否发生改变的问题也就是应用上述检验方法进行检验。, http://www.100md.com
2 实例应用
例 某医院为了评价某治疗方案是否能有效控制4～5岁儿童癫痫发病情况，在考虑和控制有关混杂因素后，随机收治了20名患有癫痫的儿童，其治疗前一年和治疗后一年的发病情况如下： 患者编号
1
2
3
4
5
6
7
8
9
, 百拇医药 10
11
12
13
14
15
16
17
18
19
20
治疗前发病次数
6
11
, 百拇医药
12
10
8
4
8
10
12
12
5
12
10
8
8
9
, 百拇医药
15
10
7
9
治疗后发病次数
8
10
7
8
9
5
7
10
7
, 百拇医药
5
4
7
10
7
7
5
9
7
9
8
治疗前平均发病次数
, 百拇医药 治疗后平均发病次数
1-0.8018=19.892%，因此治疗后的发病次数与治疗前发病次数相比，下降了19.892%。。因为|Z|>1.96，对应的P<0.05，所以拒绝无效假设H0∶β=0，因此可以认为治疗后癫痫发病次数比治疗前有显著下降(控制癫痫发作的疗效是显著的)。3 讨论本文给出Poisson分布资料前后对照的检验方法和例子，eβ是治疗后发病次数的总体均数与治疗前发病次数的总体均数之比。在实际应用时，应注意混杂因素对结果的影响，特别如年龄等混杂因素的影响。在可能的情况下，应采用随机对照试验(Random Control Trial, RCT)设计进行疗效评价研究，并通过随机分组平衡可能的混杂因素影响。由于篇幅所限，对于RCT设计的疗效评价研究中Poisson分布资料，作者只能在另文中论述。
参 考 文 献
1，Dobson AJ, An Introduction to Generalized Linear Models, Printed in Great Britain by T. J. Press(Padstow) Ltd, Padstow, Gornwall in 1991.
2，金丕焕.医用统计方法.上海医科大学出版社，1992.
收稿日期：2000-01-21, 百拇医药