基于可变形表面模型的MR图像脑表面形态提取
作者:罗述谦 闫华
单位:首都医科大学生物医学工程系
关键词:可变形表面;皮质;MR图像
首都医科大学学报990103 提要: 探讨了大脑表面形态提取的一种新方法可变形表面模型。脑表面形态的提取是脑的可视化、形态学分析、脑图像配准等多种工作的基础。对于多层MR脑图像,应用可变形表面算法,可以较准确地获得脑外部皮质的参数化表示。该算法对噪声具有一定的鲁棒性,并对于不同的外部形态具有较大范围的适应性。
中图分类号: R318.5
Based on Deformable Surface Model Morphology Extraction of Cortical Surface in MR Images
, 百拇医药
Luo Shuqian, Yan Hua
Department of Biomedical Engineering, Capital University of Medical Sciences
Abstract: As a new method to map the outer cortex of the human brain, a deformable surface model is described in this paper. Obtaining the shape of the brain is an important step for shape visualization, morphological analysis and registration of brain images.Using the deformable surface algorithm on three-dimensional MR images a parametererization of the central layer of the outer cortex can be obtained. This algorithm combines robustness to noise with flexibility to represent a broad class of shapes.
, 百拇医药
Key words: deformable surface; cortex; magnetic resonance image
在图像处理领域,二维和三维图像边界提取作为形态的可视化和分析工作中非常关键的一步,被大家广泛关注和研究。通常采用的3种方法:边缘提取和连接、轮廓跟踪及手绘各有其不足之处。第1种方法存在着过多或者过少的边界点的识别与连接问题;轮廓跟踪法不易确定合适的边界条件;而手绘法则需要大量的时间,无自动性,不可重复。针对这3种方法的不足,可变形表面模型既具有抗噪声性又对各种形状的变化能灵活适应。三维空间中的可变形表面模型是二维中边界提取的活动轮廓模型的扩展[1]。
可变形表面如同一个弹性的布单,可以是闭合的,也可以是开放的。开始时我们将它放置于感兴趣的边界附近,在图像数据产生的外力和表面上点与点之间的弹性内力的共同作用下,可变形表面向着要提取的边界逐步靠近。经过数次变形之后,外力与内力的总和为零,可变形表面满足力的平衡方程,这时它已紧紧贴着我们所要提取的边界,变形终止。这一系列过程可以归纳为一个可变形表面算法,即deformable surface algorithm(DFSA)[2]。
, 百拇医药
我们的研究目的是利用DFSA算法获取脑皮质的中间层的参数化表示。
在用DFSA算法获取皮质中间层之后,可以采用控制点法深入脑的沟、裂(深度定位),并计算曲率(曲率定位),不同的曲率反映不同的沟回结构,从而更准确、全面地反映脑表面的形态。
1 原理和方法
1.1 皮质壳层与质量函数
在讲述可变形表面算法之前,先看一看脑的解剖结构。脑组织按成分分为灰质、白质、脑脊液和皮层脂肪。皮质由灰质组成,是高度卷曲的包绕着绝大部分脑组织的薄层,它的厚度大致均匀。我们所要提取的表面便是皮质的中间层。
我们用C来表示皮质薄壳,厚度记为w。将α(u,v)作为C的中间层的参数化表示(图1),Nα(u,v)表示α(u,v)的法向量,则C可以精确地表示为:
, 百拇医药
C={X∈IR3|X=α(u,v)+λNα(u,v),
(1)
图1 三维空间中薄壳C的中心到二维平面D的映射
在这里,D是α(u,v)的定义域。
应用DFSA之前,需要先对图像进行预处理。即在体积数据集V中,对每一点X∈V,以质量函数m(X)表示点X属于C的概率。质量函数一般为二值函数: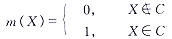
(2)
, 百拇医药
描述了质量函数之后,我们再来看可变形表面,它是1个闭合的表面,用X(u,v)=[x(u,v),y(u,v),z(u,v)]表示,定义于二维区域D。
1.2 力学模型
1.2.1 外力 外力由质心力和法向力2个成分构成,将表面拉向α(u,v)。
质心力来自图像数据,记为F1(X)。为定义这部分外力,先定义μ(X)为C包含在点X的球形邻域N(半径为ρ)内的质量,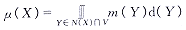
(3)
定义质心为包含在N(X)∩V内的质量μ(X)的中心,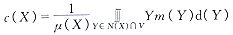
, http://www.100md.com
(4)
可以看出,如果邻域的半径 ,位于α(u,v)上的点的质心就是它本身(图2)。相应地,定义作用于点X的外力F1(X)为来自c(X)的吸引力,F1(X)=c(X)-X
,位于α(u,v)上的点的质心就是它本身(图2)。相应地,定义作用于点X的外力F1(X)为来自c(X)的吸引力,F1(X)=c(X)-X
(5)
图2 质心力图示
法向力是当球形邻域与C不相交,F1(X)不起作用时将可变形表面上的点向C拉近的力,等于γ(u,v)N(u,v),N(u,v)为表面的法向量,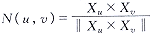
, 百拇医药
(6)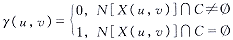
(7)
1.2.2 内力 内力为弹性力,维持表面变形过程中点与点之间的连续性,由β(u,v)加权。
(8)
1.2.3 力的平衡方程 在外力和内力的共同作用下,可变形表面像1个收缩或扩展的弹性膜一样,不断向α(u,v)靠近,经一系列变形后收敛于1个平衡状态,满足如下微分方程:
β(u,v)〔Xuu(u,v)+Xvv(u,v)〕+〔1-y(u,v)〕{c〔X(u,v)〕-X(u,v)}+γ(u,v)N(u,v)=0
, 百拇医药
(9)
1.3 迭代求解
为解方程(9),通过把D划分为(2N×N)个小正方形将矢量函数X(u,v)离散化,并用差分来近似微分,运用逐次松弛法得出迭代公式: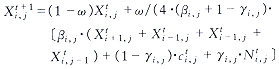
(10)
2 实验
本次实验选取25张头部横断面的MR图像(大小为256像素×256像素)进行处理。
首先进行预处理。预处理是非常关键的1个步骤,也是个比较困难的问题。文献[2]运用三维图像分割法,分两步来决定质量函数:第一步运用形态学的腐蚀法将脑组织与周围的骨、皮肤与脂肪分开,用形态学的扩展捕获在腐蚀中丢失的脑组织;第二步,应用基于Markov随机场的分割方法来分离灰质与白质和脑脊液,得到1个灰质的二值的指示函数。这一方法很复杂,需要运用许多形态学和图像处理方面的知识。这里,我们通过一种简单的方法进行预处理。对每张图,将头皮、颅骨去除,再从脑组织中提取宽度为20像素的带状区域(包含灰质和白质)(图3)。不同于文献[2]中所用的只能取0或1的二值质量函数(称为“硬分割”),该法要用到复杂的脑组织概率分布知识及图像预处理[3]。我们采用“软分割”的方法定义质量函数m(X),对提取的带状部分作灰度直方图,依此定义1个在0到1之间取值的质量函数。
, http://www.100md.com
图3 宽度为20像素的灰、白质带
构建1个层数为60的体积文件,处理过的MR图像位于第20到44层的位置。由于层数较少、脑的外型尺寸变化不大,将可变形表面初始化为一个圆柱,高度30像素,半径110像素。圆柱的中心定在x0=128,y0=128,z0=32。
柱坐标系中的点可以表示为:
(11)
体积文件中圆柱上点的坐标基于(11)式,但做了一定改动。
对于25层MR图像的情况,由于X(u,v)的定义域D横向与纵向比大于2,因此将D分成M×N个小正方形,M=100,N=12(M为横向,N为纵向)。即i∈〔0,1,…,100〕,j∈〔0,1,…,12〕,i对应于纬度角,j对应于Z值,每间隔1层有M个初始点。表面提取结果如图4所示。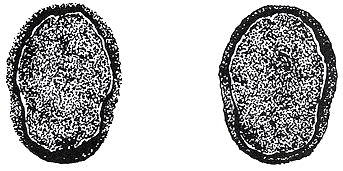
, 百拇医药
图4 应用DFSA后的2张不同层面的MR图像
左图:MR07,右图:MR15
通常迭代运算量很大,为减少运算时间,这里采用多尺度法。即初始时M和N比较小,DFSA能较快地收敛,使可变形表面大致包绕皮质的中间层;然后再增大M和N,继续计算。由于以低分辨率的处理结果为初始值,所以高分辨率下能很快地收敛。由低分辨率向高分辨率的转化采用差值法在2个参数坐标相邻点的中间插入新点,或者将新点放在1个点的最邻近位置处。
将球形邻域N的半径定为3像素。在DFSA中,多次对N(X)∩V是否为空集(即可变形表面上的点的邻域是否与C相交)进行判断,我们用flag(X)作为标识,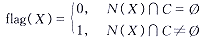
(12)
, http://www.100md.com
[法1]:可以简单地用N(X)∩C内的质量μ(X)与1的比较来判断,μ(X)大于或等于1时认为相交。预处理中,有时会将噪声误认为是灰质,有时又可能将灰质判断为噪声。由于我们的算法运用了积分,所以对噪声有一定的鲁棒性。但遇到被判为灰质的较密集的噪声时,用此法有时仍会错判。
[法2]:设一阈值t(t>1,一般可以取[10,30]之内的值),μ(X)≥t时认为相交。即在X与C相交很少时仍以法向力和L0加权的内力作用于X,将X拉向α(u,v)。这样的处理,不仅可以略过分散的噪声点,对一些较密集的噪声也能较好地抑制,弥补了不太精确的预处理带来的错误。如图4中左上方靠近皮质的白块包围的一些像素灰度与皮质灰度相似,难以用简单的预处理去掉,用此法可以使其不对结果的准确性产生影响。
定义停止迭代的判据为: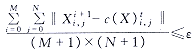
, 百拇医药
(13a)
或者
(13b)
取K0=5×10-5,L0=2×10-4时,经30~40次迭代,可变形表面收敛于1个平衡形态,迭代终止。
3 结果和讨论
在预处理中定义质量函数时,我们采用了软分割,适于灰质与白质灰度分界不够明显的特点,又比较适合有噪声的情况。这是硬分割所不能及的。
DFSA中2个重要的参数为K0和L0。K0和L0是内力的加权系数,当可变形表面离C比较远时和表面上点的邻域切割C时外力不同,前者为法向力γ(X)N(X),后者为质心力F(X)=c(X)-X。相应地,前一种情况下,内力的加权系数为L0,后一种情况下为K0。由此可见,离C较远时,可变形表面的弹性行为依赖于L0,经数次变形后表面与皮质很接近时K0起作用,最终的形态几乎完全由质心力和K0加权的弹性力所决定。L0的作用在于保证变形的平滑。实验中发现,L0越大,可变形表面的收缩速度越慢,L0越小则收缩速度越快。但不能为加快速度而使L0过小,这样可能点从皮质外一下子跳到皮质内部,进一步远离皮质的中间层,出现严重错误。K0和L0都对点分布的均匀性有影响,2个值过小时,点的分布不够均匀。定量研究发现,K0在10-4以下DFSA的结果比较稳定,超过这一数值时结果显著恶化;当L0在较大的范围内(10-5~10-3)变化时结果基本稳定。
, http://www.100md.com
综上可以看出,利用可变形表面模型提取脑表面形态,其结果在很大程度上依赖于预处理。预处理若能准确地将灰质与别的成分分离,那么,运用该算法便能得到准确的皮质中心层的参数化表示;如果预处理做得不够好,得到的中心层也不够精确。因此,预处理是一个关键的步骤,对结果的准确性有重要的影响。
尽管对预处理有较高的要求是DFSA的一个局限之处,它仍然具有许多优点:①可变形表面模型初始为一个面,在向最终的解迭代变形过程中始终保持为一个曲面,因此,曲面的性质,如法向量、曲率等可以被估算。②外力的计算运用图像数据的积分而不是差分,这就使算法对噪声具有一定程度的鲁棒性。③对较大范围的形状变化能灵活适应。
应用可变形表面算法获得皮质中间层的参数化表示之后,再利用深度定位和曲率计算就能对大脑形态有准确的描述。一些显著的解剖特征如半球间裂、中央沟、枕叶等都能识别出来,从而能为图像的自动特征识别及匹配等工作所用。
, 百拇医药 北京市教委科技发展计划资助项目
参考文献
1 Davatzikos C A, Prince J L. An active contour model for mapping the cortex. IEEE Trans Med Imag, 1995,14:3
2 Davatzikos I C, Bryan R N. Using a deformable surface model to obtain a shape representation of the cortex. IEEE Trans Med Imag, 1996,15:12
3 Evans A C, Kamber M, Collins D L, et al. An MRI-based probabilistic atlas of neuroanatomy. In: Shprovon S D,ed. Megnetic Resonance Scanning and Elilepsy. New York: Plenum Press, 1994. 263
收稿日期:1998-09-11, http://www.100md.com
单位:首都医科大学生物医学工程系
关键词:可变形表面;皮质;MR图像
首都医科大学学报990103 提要: 探讨了大脑表面形态提取的一种新方法可变形表面模型。脑表面形态的提取是脑的可视化、形态学分析、脑图像配准等多种工作的基础。对于多层MR脑图像,应用可变形表面算法,可以较准确地获得脑外部皮质的参数化表示。该算法对噪声具有一定的鲁棒性,并对于不同的外部形态具有较大范围的适应性。
中图分类号: R318.5
Based on Deformable Surface Model Morphology Extraction of Cortical Surface in MR Images
, 百拇医药
Luo Shuqian, Yan Hua
Department of Biomedical Engineering, Capital University of Medical Sciences
Abstract: As a new method to map the outer cortex of the human brain, a deformable surface model is described in this paper. Obtaining the shape of the brain is an important step for shape visualization, morphological analysis and registration of brain images.Using the deformable surface algorithm on three-dimensional MR images a parametererization of the central layer of the outer cortex can be obtained. This algorithm combines robustness to noise with flexibility to represent a broad class of shapes.
, 百拇医药
Key words: deformable surface; cortex; magnetic resonance image
在图像处理领域,二维和三维图像边界提取作为形态的可视化和分析工作中非常关键的一步,被大家广泛关注和研究。通常采用的3种方法:边缘提取和连接、轮廓跟踪及手绘各有其不足之处。第1种方法存在着过多或者过少的边界点的识别与连接问题;轮廓跟踪法不易确定合适的边界条件;而手绘法则需要大量的时间,无自动性,不可重复。针对这3种方法的不足,可变形表面模型既具有抗噪声性又对各种形状的变化能灵活适应。三维空间中的可变形表面模型是二维中边界提取的活动轮廓模型的扩展[1]。
可变形表面如同一个弹性的布单,可以是闭合的,也可以是开放的。开始时我们将它放置于感兴趣的边界附近,在图像数据产生的外力和表面上点与点之间的弹性内力的共同作用下,可变形表面向着要提取的边界逐步靠近。经过数次变形之后,外力与内力的总和为零,可变形表面满足力的平衡方程,这时它已紧紧贴着我们所要提取的边界,变形终止。这一系列过程可以归纳为一个可变形表面算法,即deformable surface algorithm(DFSA)[2]。
, 百拇医药
我们的研究目的是利用DFSA算法获取脑皮质的中间层的参数化表示。
在用DFSA算法获取皮质中间层之后,可以采用控制点法深入脑的沟、裂(深度定位),并计算曲率(曲率定位),不同的曲率反映不同的沟回结构,从而更准确、全面地反映脑表面的形态。
1 原理和方法
1.1 皮质壳层与质量函数
在讲述可变形表面算法之前,先看一看脑的解剖结构。脑组织按成分分为灰质、白质、脑脊液和皮层脂肪。皮质由灰质组成,是高度卷曲的包绕着绝大部分脑组织的薄层,它的厚度大致均匀。我们所要提取的表面便是皮质的中间层。
我们用C来表示皮质薄壳,厚度记为w。将α(u,v)作为C的中间层的参数化表示(图1),Nα(u,v)表示α(u,v)的法向量,则C可以精确地表示为:
, 百拇医药
C={X∈IR3|X=α(u,v)+λNα(u,v),

(1)

图1 三维空间中薄壳C的中心到二维平面D的映射
在这里,D是α(u,v)的定义域。
应用DFSA之前,需要先对图像进行预处理。即在体积数据集V中,对每一点X∈V,以质量函数m(X)表示点X属于C的概率。质量函数一般为二值函数:
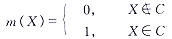
(2)
, 百拇医药
描述了质量函数之后,我们再来看可变形表面,它是1个闭合的表面,用X(u,v)=[x(u,v),y(u,v),z(u,v)]表示,定义于二维区域D。
1.2 力学模型
1.2.1 外力 外力由质心力和法向力2个成分构成,将表面拉向α(u,v)。
质心力来自图像数据,记为F1(X)。为定义这部分外力,先定义μ(X)为C包含在点X的球形邻域N(半径为ρ)内的质量,
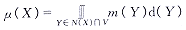
(3)
定义质心为包含在N(X)∩V内的质量μ(X)的中心,
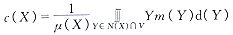
, http://www.100md.com
(4)
可以看出,如果邻域的半径
 ,位于α(u,v)上的点的质心就是它本身(图2)。相应地,定义作用于点X的外力F1(X)为来自c(X)的吸引力,F1(X)=c(X)-X
,位于α(u,v)上的点的质心就是它本身(图2)。相应地,定义作用于点X的外力F1(X)为来自c(X)的吸引力,F1(X)=c(X)-X(5)

图2 质心力图示
法向力是当球形邻域与C不相交,F1(X)不起作用时将可变形表面上的点向C拉近的力,等于γ(u,v)N(u,v),N(u,v)为表面的法向量,
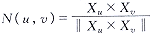
, 百拇医药
(6)
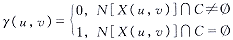
(7)
1.2.2 内力 内力为弹性力,维持表面变形过程中点与点之间的连续性,由β(u,v)加权。

(8)
1.2.3 力的平衡方程 在外力和内力的共同作用下,可变形表面像1个收缩或扩展的弹性膜一样,不断向α(u,v)靠近,经一系列变形后收敛于1个平衡状态,满足如下微分方程:
β(u,v)〔Xuu(u,v)+Xvv(u,v)〕+〔1-y(u,v)〕{c〔X(u,v)〕-X(u,v)}+γ(u,v)N(u,v)=0
, 百拇医药
(9)
1.3 迭代求解
为解方程(9),通过把D划分为(2N×N)个小正方形将矢量函数X(u,v)离散化,并用差分来近似微分,运用逐次松弛法得出迭代公式:
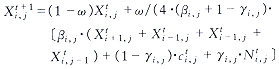
(10)
2 实验
本次实验选取25张头部横断面的MR图像(大小为256像素×256像素)进行处理。
首先进行预处理。预处理是非常关键的1个步骤,也是个比较困难的问题。文献[2]运用三维图像分割法,分两步来决定质量函数:第一步运用形态学的腐蚀法将脑组织与周围的骨、皮肤与脂肪分开,用形态学的扩展捕获在腐蚀中丢失的脑组织;第二步,应用基于Markov随机场的分割方法来分离灰质与白质和脑脊液,得到1个灰质的二值的指示函数。这一方法很复杂,需要运用许多形态学和图像处理方面的知识。这里,我们通过一种简单的方法进行预处理。对每张图,将头皮、颅骨去除,再从脑组织中提取宽度为20像素的带状区域(包含灰质和白质)(图3)。不同于文献[2]中所用的只能取0或1的二值质量函数(称为“硬分割”),该法要用到复杂的脑组织概率分布知识及图像预处理[3]。我们采用“软分割”的方法定义质量函数m(X),对提取的带状部分作灰度直方图,依此定义1个在0到1之间取值的质量函数。

, http://www.100md.com
图3 宽度为20像素的灰、白质带
构建1个层数为60的体积文件,处理过的MR图像位于第20到44层的位置。由于层数较少、脑的外型尺寸变化不大,将可变形表面初始化为一个圆柱,高度30像素,半径110像素。圆柱的中心定在x0=128,y0=128,z0=32。
柱坐标系中的点可以表示为:

(11)
体积文件中圆柱上点的坐标基于(11)式,但做了一定改动。
对于25层MR图像的情况,由于X(u,v)的定义域D横向与纵向比大于2,因此将D分成M×N个小正方形,M=100,N=12(M为横向,N为纵向)。即i∈〔0,1,…,100〕,j∈〔0,1,…,12〕,i对应于纬度角,j对应于Z值,每间隔1层有M个初始点。表面提取结果如图4所示。

, 百拇医药
图4 应用DFSA后的2张不同层面的MR图像
左图:MR07,右图:MR15
通常迭代运算量很大,为减少运算时间,这里采用多尺度法。即初始时M和N比较小,DFSA能较快地收敛,使可变形表面大致包绕皮质的中间层;然后再增大M和N,继续计算。由于以低分辨率的处理结果为初始值,所以高分辨率下能很快地收敛。由低分辨率向高分辨率的转化采用差值法在2个参数坐标相邻点的中间插入新点,或者将新点放在1个点的最邻近位置处。
将球形邻域N的半径定为3像素。在DFSA中,多次对N(X)∩V是否为空集(即可变形表面上的点的邻域是否与C相交)进行判断,我们用flag(X)作为标识,
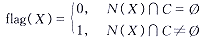
(12)
, http://www.100md.com
[法1]:可以简单地用N(X)∩C内的质量μ(X)与1的比较来判断,μ(X)大于或等于1时认为相交。预处理中,有时会将噪声误认为是灰质,有时又可能将灰质判断为噪声。由于我们的算法运用了积分,所以对噪声有一定的鲁棒性。但遇到被判为灰质的较密集的噪声时,用此法有时仍会错判。
[法2]:设一阈值t(t>1,一般可以取[10,30]之内的值),μ(X)≥t时认为相交。即在X与C相交很少时仍以法向力和L0加权的内力作用于X,将X拉向α(u,v)。这样的处理,不仅可以略过分散的噪声点,对一些较密集的噪声也能较好地抑制,弥补了不太精确的预处理带来的错误。如图4中左上方靠近皮质的白块包围的一些像素灰度与皮质灰度相似,难以用简单的预处理去掉,用此法可以使其不对结果的准确性产生影响。
定义停止迭代的判据为:
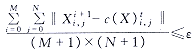
, 百拇医药
(13a)
或者

(13b)
取K0=5×10-5,L0=2×10-4时,经30~40次迭代,可变形表面收敛于1个平衡形态,迭代终止。
3 结果和讨论
在预处理中定义质量函数时,我们采用了软分割,适于灰质与白质灰度分界不够明显的特点,又比较适合有噪声的情况。这是硬分割所不能及的。
DFSA中2个重要的参数为K0和L0。K0和L0是内力的加权系数,当可变形表面离C比较远时和表面上点的邻域切割C时外力不同,前者为法向力γ(X)N(X),后者为质心力F(X)=c(X)-X。相应地,前一种情况下,内力的加权系数为L0,后一种情况下为K0。由此可见,离C较远时,可变形表面的弹性行为依赖于L0,经数次变形后表面与皮质很接近时K0起作用,最终的形态几乎完全由质心力和K0加权的弹性力所决定。L0的作用在于保证变形的平滑。实验中发现,L0越大,可变形表面的收缩速度越慢,L0越小则收缩速度越快。但不能为加快速度而使L0过小,这样可能点从皮质外一下子跳到皮质内部,进一步远离皮质的中间层,出现严重错误。K0和L0都对点分布的均匀性有影响,2个值过小时,点的分布不够均匀。定量研究发现,K0在10-4以下DFSA的结果比较稳定,超过这一数值时结果显著恶化;当L0在较大的范围内(10-5~10-3)变化时结果基本稳定。
, http://www.100md.com
综上可以看出,利用可变形表面模型提取脑表面形态,其结果在很大程度上依赖于预处理。预处理若能准确地将灰质与别的成分分离,那么,运用该算法便能得到准确的皮质中心层的参数化表示;如果预处理做得不够好,得到的中心层也不够精确。因此,预处理是一个关键的步骤,对结果的准确性有重要的影响。
尽管对预处理有较高的要求是DFSA的一个局限之处,它仍然具有许多优点:①可变形表面模型初始为一个面,在向最终的解迭代变形过程中始终保持为一个曲面,因此,曲面的性质,如法向量、曲率等可以被估算。②外力的计算运用图像数据的积分而不是差分,这就使算法对噪声具有一定程度的鲁棒性。③对较大范围的形状变化能灵活适应。
应用可变形表面算法获得皮质中间层的参数化表示之后,再利用深度定位和曲率计算就能对大脑形态有准确的描述。一些显著的解剖特征如半球间裂、中央沟、枕叶等都能识别出来,从而能为图像的自动特征识别及匹配等工作所用。
, 百拇医药 北京市教委科技发展计划资助项目
参考文献
1 Davatzikos C A, Prince J L. An active contour model for mapping the cortex. IEEE Trans Med Imag, 1995,14:3
2 Davatzikos I C, Bryan R N. Using a deformable surface model to obtain a shape representation of the cortex. IEEE Trans Med Imag, 1996,15:12
3 Evans A C, Kamber M, Collins D L, et al. An MRI-based probabilistic atlas of neuroanatomy. In: Shprovon S D,ed. Megnetic Resonance Scanning and Elilepsy. New York: Plenum Press, 1994. 263
收稿日期:1998-09-11, http://www.100md.com