适于图像型微粒检测的自适应滤波新方法*
作者：杨成胡 陈光杰 樊英杰
单位：第一军医大学 (510515)
关键词：自适应滤波；中值滤波；OS滤波；α均值滤波；反α均值滤波；局部直方图
中国医疗器械杂志990203 提要 基于其局部灰度直方图，提出了一种新的适用于图像型微粒检测的自适应噪声滤波方法。它由中值滤波和特殊的OS滤波(即α均值滤波、反α均值滤波)等基本滤波器构成。此滤波器在噪声滤除和图像边缘保持两方面都有较满意的性能，而且能简单快速地实现。文中给出了实验的结果。
A New Adaptive Filtering Method for
Micro-Particle Image Processing
Yang Chenghu Chen Guangjie Fan Yingjie
, 百拇医药
The First Military Medical University
ABSTRACT Based on the local gray level histogram of macro-particle image which is more special than other images, a new adaptive noise filtering method for macro-particle image processing is developed and described in this paper. It is made up of median filter and special order statistic(OS) filters (α-mean filter and inverse α-mean filter).This adaptive filter not only has satisfactory performance in both of noise-removal and edge-preservation of macro-particle image,but also is easy and quick to implement. An example is presented in this paper.
, 百拇医药
KEY WORDS Adaptive filtering Median filter OS filter α-mean filter Inverse α-mean filter Local histogram
微粒检测广泛应用于医学及临床的许多领域[6]。近年来，由于CCD技术和计算机数字图像处理、分析技术的迅速发展，人们愈来愈乐意于采用CCD和数字图像处理方法来进行微粒的检测和分析[4]，即图像型微粒的检测。
图像型微粒的检测中最关键的是图像的正确分割。由于实际的微粒图像往往受噪声污染，微粒与背景对应的灰度级变得较模糊，不能直接进行正确的图像分割，因此，在图像分割(即二值化)之前，必须进行必要的预处理，即滤波处理[5]。正确的图像分割一般是指确保微粒的数量、尺寸和形态等信息，不失真地将微粒从背景中提取出来。因此，就要求预处理滤波能有效地滤除噪声的同时，兼有良好的保图像边缘的性能。
, 百拇医药
《药典》上对静脉注射药剂中的悬浮微粒的尺寸和数目都有严格的要求和规定，目前国内普遍采用效率低、不可靠的“人工灯检法”，进行产品质量检验和控制。为提高生产效率和可靠性，实现产品质量检验的自动化，我们正研制一种自动检测系统。该检测系统的核心就是微粒的计数和尺寸信息的检测。其显著特点是：微粒图像中噪声结构较复杂化，既有高斯型噪声，也有脉冲型噪声，且信噪较低；微粒尺寸也较小；而且是一种生产线在线检测系统，因此，要求处理速度快。研制过程中的实践证明，现有的各种滤波方法往往不能同时兼顾上述三方面的性能，尤其是实现速度难兼顾[1][2][5]。
基于上述缘由，针对微粒图像的特性，本文研究并提出一种较简便的自适应滤波方法，具体地讲，就是根据图像局部直方图特点，自适应地进行α均值滤波、反α均值滤波或中值滤波。其特点是不仅有滤波和保持微粒边缘的两方面良好的性能，而且实现简单、速度快，完全可用DSP或FPGA实现。
1 基本滤波器简介
, 百拇医药
在介绍本文所提出的自适应滤波方法之前，先须简要介绍它所包含的几种基本滤波器的概念与特性，即中值滤波、α均值滤波和反α均值滤波等。
1.1 中值滤波
所谓中值滤波就是用处理窗口中各象素的灰度级中间值作为滤波器的输出，主要是针对随机脉冲型噪声的一种滤波方法。中值滤波具有能保持轮廓边缘清晰度的显著优点，但存在在抑制噪声的同时也会对信号产生抑制的不足、以及对于某些作用形式较为缓和的干扰或噪声效果较差的缺点[3]、[5]。
1.2 滤波
普通的局部均值滤波虽然简单易实现，且对随机的互不相关、均值为零的高斯噪声等的平滑效果较好，但对脉冲型噪声很敏感，平滑效果差，而且会使图像变模糊，特别是使图像边缘变得不清晰[2][5]。为同时获得较理想的滤除各种噪声和保持图像边缘的性能，人们研究并提出了一些新的均值滤波方法。由Bovik等提出的OS滤波[3]就是其中的一种，其基本思想是先将窗口内象素按灰度级进行排序，再取部分象素的某种线性平均：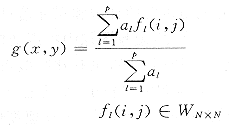
(1)
, http://www.100md.com
其中，fl(i,j)是滤波窗口WN×N内的第l个最小灰度值，而g(x,y)为窗口中心的滤波输出值，一般取P2，{al}为系数，具体的OS滤波形式就由{al}决定，其实算术平均和中值滤波都是OS滤波的特例。
1.2.1 α均值滤波
α均值滤波是一种特殊部的OS滤波法[1]，具体就是，取系数为：
(2)
即只取窗口内p个最小灰度的象素点进行算术平均的滤波方法，其中参加平均的象素数占处理窗口内总象素数的比率为α。其特点是在普通均值滤波的基础上，增强了对脉冲型噪声的滤除能力。但仍属平均法，依旧存在模糊边缘的缺点。
, 百拇医药
1.2.2 反α均值滤波
反α均值滤波中，系数{al}的取法恰好与α均值滤波相反，即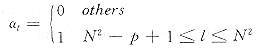
(3)
同样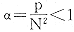
，即只取窗口内p个最大灰度的象素点进行算术平均的滤波方法，其中参加平均的象素数占处理窗口内总象素数的比率仍为α。这是本文针对当滤波处理窗口滑动到微粒上时，提出的一种特殊的均值滤波法。为方便起见，称之为“反α均值滤波”。
2 基于局部直方图的自适应滤波方法
2.1 微粒图象中局部直方图的特点
微粒图像仅由两类区域组成，即背景和微粒。当处理窗口移动时，将处理三种类型的局部区域(简称局域)，即背景域、微粒域和两者间的边缘域。
, 百拇医药
理想的微粒图像中，背景和微粒分别对应不同灰度级范围(二值图像只有两个灰度级)且此两个灰度级范围相距有一定的距离[5]，因此，上述三类局域的局部直方图完全不同，如图1所示。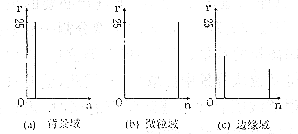
图1 理想微粒图像的局部直方图(统计窗口为5×5)
通过CCD所获取的实际微粒图像虽因噪声的介入及其它因素，两类区域对应的灰度级范围发生了重叠现象(主要是背景区域上分布有对应于微粒的灰度级)，但三类局域的局部直方图依然具有较明显的区别，类似理想情况。图2为典型的药剂中悬浮微粒图像的局部直方图。值得说明的是，图2是将8bits的灰度值经四舍五入取成10的倍数后统计得来的，且>90的值皆取为90，这是因为图像中的灰度值基本集中在0～90的范围内。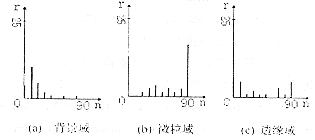
, 百拇医药
图2 实际微粒图像的局部直方图(统计窗口为5×5)
2.2 基于局部直方图的自适应滤波方法
滤波处理的根本目的是为增大微粒和背景的灰度差，以便于图像分割处理[5]。换句话，经滤波处理后，要求背景域的灰度值尽可能小，而微粒具有尽量大的灰度值，二者间的边缘力求清晰。若针对三种不同特点的区域，分别采取不同的滤波处理方法，即背景域采用α均值滤波，微粒域取反α均值滤波，而边缘处进行中值滤波，就可达到目的。局部直方图就为实现该自适应滤波所需的区域判别提供了依据。这就是基于局部直方图的自适应滤波方法的基本思想。此中也包含了本文之所以提出所谓的“反α均值滤波”的缘由。
显然，实现此自适应滤波的关键是如何根据局部直方图进行区域判别。实际上有多种判别方法，最简单的方法是先设定一灰度阀值(设为T)，然后统计滤波处理窗口内灰度值≥或1和N2表示)，若N1/(N1+N2)≥α(α为一比率)，则为微粒域；而当N2/(N1+N2)≥α时，就是背景域；都不满足时，就归于边缘域。阀值T既可用实验选定，也可从微粒图像的整体直方图中得到；而参数α一般需通过实验来确定。
, http://www.100md.com
处理窗口大小的选择，也直接影响到滤波器的性能。现设为N×N，一般N与图像中微粒的大小及噪声的特点有关，而且为能更好地保持边缘，中值滤波窗口应取小些[2]。因此，基于局部直方图的自适应滤波可用下式表示，即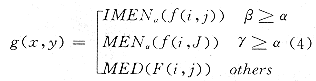
式中(i,j)∈WN×N；(x,y)为处理窗口WN×N的中心象素点；MENα()、IMENa()和MED()分别表示α均值滤波、反α均值滤波和中值滤波；f(i,j)和g(x,y)分别表示原始图象及滤波输出；而
β=N1/N2； γ=N2/N2
由于各基本滤波器均有简单而快速的实现算法[1][7][8]，此自适应滤波就完全能简单且快速地得以实现。
, 百拇医药
3 实验结果及结论
3.1 实验结果
图3(a)为一幅通过CCD所获取的透明药剂中悬浮微粒的原始数字微粒图像，图3(b)、(c)及(d)分别为采用α均值滤波、中值滤波和自适应滤波后的同一阀值二值化结果。实验中，灰度分辨率为8bits，处理窗口取为5×5(中值滤波窗口取为3×3)、α=0.8。
3.2 结论
从实验结果中可见：简单的中值滤波保边缘好，但对噪声的抑制不够，造成二值化图像中有虚假的微粒出现；α均值滤波虽然能很好地抑制噪声，却造成微粒图像的边缘模糊，如图3(c)中，两个相距较近的微粒就因滤波后边缘变模糊，无法分割而连成一体，且形态失真较大；而自适应滤波既能很好地抑制噪声，又保持较好的边缘特性。该自适应滤波器的实现简单且有快速算法，完全可用DSP、FPGA等来实现[8]，在药剂悬浮微粒的在线自动检测系统中，我们采用FPGA和DSP的综合实现法，速度完全满足要求。
, 百拇医药
图3 药剂中悬浮微粒图像中的滤波处理的实验结果
因此，基于局部直方图的自适应滤波方法是一种既有效又实用的预处理滤波方法。
*广东省科学基金资助课题
参 考 文 献
1.程存学等.计算机视觉—低层处理技术.电子工业出版社，1993
2.X.Z.Sun.Anastasios N. Venetsanopoulos.Adaptiveschemes for noise filtering and edge detection by use of local statistics.IEEE Trans.on circuits and system,1988,35(1):57-69
, 百拇医药
3.A.C.Bovik,T.S.Huang,and D.C.Munson.A generalization of median filtering using linear combinations of order statistices.IEEE Trans. Acoust.,Speech,Signal Processing,1983,ASSP-31(12):1342-1349
4.王庆有等.CCD应用技术.天津大学出版社，1993.
5.周新伦等.数字图象处理.国防工业出版社，1988.
6.汤耀法等.计算机应用与软件.1996，13(1) 17-21
7.Thomas S. Huang,George J.Yang,Gregory Y. Tang.A fast two-dimensionalMedian filtering algorithm.IEEE Trans. Acoust.,Speech,Singal Procesing,1979,ASSP-27(1)：13-18
8.余小游等.电子技术应用.1997，(11)：35-38
(1998年5月7日收稿), 百拇医药
单位：第一军医大学 (510515)
关键词：自适应滤波；中值滤波；OS滤波；α均值滤波；反α均值滤波；局部直方图
中国医疗器械杂志990203 提要 基于其局部灰度直方图，提出了一种新的适用于图像型微粒检测的自适应噪声滤波方法。它由中值滤波和特殊的OS滤波(即α均值滤波、反α均值滤波)等基本滤波器构成。此滤波器在噪声滤除和图像边缘保持两方面都有较满意的性能，而且能简单快速地实现。文中给出了实验的结果。
A New Adaptive Filtering Method for
Micro-Particle Image Processing
Yang Chenghu Chen Guangjie Fan Yingjie
, 百拇医药
The First Military Medical University
ABSTRACT Based on the local gray level histogram of macro-particle image which is more special than other images, a new adaptive noise filtering method for macro-particle image processing is developed and described in this paper. It is made up of median filter and special order statistic(OS) filters (α-mean filter and inverse α-mean filter).This adaptive filter not only has satisfactory performance in both of noise-removal and edge-preservation of macro-particle image,but also is easy and quick to implement. An example is presented in this paper.
, 百拇医药
KEY WORDS Adaptive filtering Median filter OS filter α-mean filter Inverse α-mean filter Local histogram
微粒检测广泛应用于医学及临床的许多领域[6]。近年来，由于CCD技术和计算机数字图像处理、分析技术的迅速发展，人们愈来愈乐意于采用CCD和数字图像处理方法来进行微粒的检测和分析[4]，即图像型微粒的检测。
图像型微粒的检测中最关键的是图像的正确分割。由于实际的微粒图像往往受噪声污染，微粒与背景对应的灰度级变得较模糊，不能直接进行正确的图像分割，因此，在图像分割(即二值化)之前，必须进行必要的预处理，即滤波处理[5]。正确的图像分割一般是指确保微粒的数量、尺寸和形态等信息，不失真地将微粒从背景中提取出来。因此，就要求预处理滤波能有效地滤除噪声的同时，兼有良好的保图像边缘的性能。
, 百拇医药
《药典》上对静脉注射药剂中的悬浮微粒的尺寸和数目都有严格的要求和规定，目前国内普遍采用效率低、不可靠的“人工灯检法”，进行产品质量检验和控制。为提高生产效率和可靠性，实现产品质量检验的自动化，我们正研制一种自动检测系统。该检测系统的核心就是微粒的计数和尺寸信息的检测。其显著特点是：微粒图像中噪声结构较复杂化，既有高斯型噪声，也有脉冲型噪声，且信噪较低；微粒尺寸也较小；而且是一种生产线在线检测系统，因此，要求处理速度快。研制过程中的实践证明，现有的各种滤波方法往往不能同时兼顾上述三方面的性能，尤其是实现速度难兼顾[1][2][5]。
基于上述缘由，针对微粒图像的特性，本文研究并提出一种较简便的自适应滤波方法，具体地讲，就是根据图像局部直方图特点，自适应地进行α均值滤波、反α均值滤波或中值滤波。其特点是不仅有滤波和保持微粒边缘的两方面良好的性能，而且实现简单、速度快，完全可用DSP或FPGA实现。
1 基本滤波器简介
, 百拇医药
在介绍本文所提出的自适应滤波方法之前，先须简要介绍它所包含的几种基本滤波器的概念与特性，即中值滤波、α均值滤波和反α均值滤波等。
1.1 中值滤波
所谓中值滤波就是用处理窗口中各象素的灰度级中间值作为滤波器的输出，主要是针对随机脉冲型噪声的一种滤波方法。中值滤波具有能保持轮廓边缘清晰度的显著优点，但存在在抑制噪声的同时也会对信号产生抑制的不足、以及对于某些作用形式较为缓和的干扰或噪声效果较差的缺点[3]、[5]。
1.2 滤波
普通的局部均值滤波虽然简单易实现，且对随机的互不相关、均值为零的高斯噪声等的平滑效果较好，但对脉冲型噪声很敏感，平滑效果差，而且会使图像变模糊，特别是使图像边缘变得不清晰[2][5]。为同时获得较理想的滤除各种噪声和保持图像边缘的性能，人们研究并提出了一些新的均值滤波方法。由Bovik等提出的OS滤波[3]就是其中的一种，其基本思想是先将窗口内象素按灰度级进行排序，再取部分象素的某种线性平均：
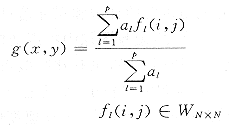(1), http://www.100md.com
其中，fl(i,j)是滤波窗口WN×N内的第l个最小灰度值，而g(x,y)为窗口中心的滤波输出值，一般取P
1.2.1 α均值滤波
α均值滤波是一种特殊部的OS滤波法[1]，具体就是，取系数为：
(2)即只取窗口内p个最小灰度的象素点进行算术平均的滤波方法，其中参加平均的象素数占处理窗口内总象素数的比率为α。其特点是在普通均值滤波的基础上，增强了对脉冲型噪声的滤除能力。但仍属平均法，依旧存在模糊边缘的缺点。
, 百拇医药
1.2.2 反α均值滤波
反α均值滤波中，系数{al}的取法恰好与α均值滤波相反，即
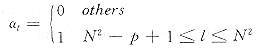(3)同样
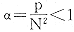，即只取窗口内p个最大灰度的象素点进行算术平均的滤波方法，其中参加平均的象素数占处理窗口内总象素数的比率仍为α。这是本文针对当滤波处理窗口滑动到微粒上时，提出的一种特殊的均值滤波法。为方便起见，称之为“反α均值滤波”。2 基于局部直方图的自适应滤波方法
2.1 微粒图象中局部直方图的特点
微粒图像仅由两类区域组成，即背景和微粒。当处理窗口移动时，将处理三种类型的局部区域(简称局域)，即背景域、微粒域和两者间的边缘域。
, 百拇医药
理想的微粒图像中，背景和微粒分别对应不同灰度级范围(二值图像只有两个灰度级)且此两个灰度级范围相距有一定的距离[5]，因此，上述三类局域的局部直方图完全不同，如图1所示。
图1 理想微粒图像的局部直方图(统计窗口为5×5)
通过CCD所获取的实际微粒图像虽因噪声的介入及其它因素，两类区域对应的灰度级范围发生了重叠现象(主要是背景区域上分布有对应于微粒的灰度级)，但三类局域的局部直方图依然具有较明显的区别，类似理想情况。图2为典型的药剂中悬浮微粒图像的局部直方图。值得说明的是，图2是将8bits的灰度值经四舍五入取成10的倍数后统计得来的，且>90的值皆取为90，这是因为图像中的灰度值基本集中在0～90的范围内。
, 百拇医药
图2 实际微粒图像的局部直方图(统计窗口为5×5)
2.2 基于局部直方图的自适应滤波方法
滤波处理的根本目的是为增大微粒和背景的灰度差，以便于图像分割处理[5]。换句话，经滤波处理后，要求背景域的灰度值尽可能小，而微粒具有尽量大的灰度值，二者间的边缘力求清晰。若针对三种不同特点的区域，分别采取不同的滤波处理方法，即背景域采用α均值滤波，微粒域取反α均值滤波，而边缘处进行中值滤波，就可达到目的。局部直方图就为实现该自适应滤波所需的区域判别提供了依据。这就是基于局部直方图的自适应滤波方法的基本思想。此中也包含了本文之所以提出所谓的“反α均值滤波”的缘由。
显然，实现此自适应滤波的关键是如何根据局部直方图进行区域判别。实际上有多种判别方法，最简单的方法是先设定一灰度阀值(设为T)，然后统计滤波处理窗口内灰度值≥或
, http://www.100md.com
处理窗口大小的选择，也直接影响到滤波器的性能。现设为N×N，一般N与图像中微粒的大小及噪声的特点有关，而且为能更好地保持边缘，中值滤波窗口应取小些[2]。因此，基于局部直方图的自适应滤波可用下式表示，即
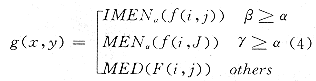
式中(i,j)∈WN×N；(x,y)为处理窗口WN×N的中心象素点；MENα()、IMENa()和MED()分别表示α均值滤波、反α均值滤波和中值滤波；f(i,j)和g(x,y)分别表示原始图象及滤波输出；而
β=N1/N2； γ=N2/N2
由于各基本滤波器均有简单而快速的实现算法[1][7][8]，此自适应滤波就完全能简单且快速地得以实现。
, 百拇医药
3 实验结果及结论
3.1 实验结果
图3(a)为一幅通过CCD所获取的透明药剂中悬浮微粒的原始数字微粒图像，图3(b)、(c)及(d)分别为采用α均值滤波、中值滤波和自适应滤波后的同一阀值二值化结果。实验中，灰度分辨率为8bits，处理窗口取为5×5(中值滤波窗口取为3×3)、α=0.8。
3.2 结论
从实验结果中可见：简单的中值滤波保边缘好，但对噪声的抑制不够，造成二值化图像中有虚假的微粒出现；α均值滤波虽然能很好地抑制噪声，却造成微粒图像的边缘模糊，如图3(c)中，两个相距较近的微粒就因滤波后边缘变模糊，无法分割而连成一体，且形态失真较大；而自适应滤波既能很好地抑制噪声，又保持较好的边缘特性。该自适应滤波器的实现简单且有快速算法，完全可用DSP、FPGA等来实现[8]，在药剂悬浮微粒的在线自动检测系统中，我们采用FPGA和DSP的综合实现法，速度完全满足要求。
, 百拇医药
图3 药剂中悬浮微粒图像中的滤波处理的实验结果
因此，基于局部直方图的自适应滤波方法是一种既有效又实用的预处理滤波方法。
*广东省科学基金资助课题
参 考 文 献
1.程存学等.计算机视觉—低层处理技术.电子工业出版社，1993
2.X.Z.Sun.Anastasios N. Venetsanopoulos.Adaptiveschemes for noise filtering and edge detection by use of local statistics.IEEE Trans.on circuits and system,1988,35(1):57-69
, 百拇医药
3.A.C.Bovik,T.S.Huang,and D.C.Munson.A generalization of median filtering using linear combinations of order statistices.IEEE Trans. Acoust.,Speech,Signal Processing,1983,ASSP-31(12):1342-1349
4.王庆有等.CCD应用技术.天津大学出版社，1993.
5.周新伦等.数字图象处理.国防工业出版社，1988.
6.汤耀法等.计算机应用与软件.1996，13(1) 17-21
7.Thomas S. Huang,George J.Yang,Gregory Y. Tang.A fast two-dimensionalMedian filtering algorithm.IEEE Trans. Acoust.,Speech,Singal Procesing,1979,ASSP-27(1)：13-18
8.余小游等.电子技术应用.1997，(11)：35-38
(1998年5月7日收稿), 百拇医药