OCT图像“双峰值效应”的维纳逆滤波恢复*
作者:向际鹰 吴震 曾绍群 骆清铭 张平 黄德修
单位:华中理工大学光电子系 (430074)
关键词:弱相干层析技术;维纳滤波;傅里叶变换;点扩展函数
中国医疗器械杂志990202 提要 分析了OCT系统中严重影响象质的“双峰值效应”,指出其起源为参考反射镜的介质高反膜,并通过建立相应的数学模型研究了其恢复的算法。从理论上推导了考虑双峰值效应后的OCT系统点扩展函数。用平均平滑周期图法分别估算出信号与噪声的功率谱密度函数。最后用维纳逆滤波算法得到恢复图象,避免了普通逆滤波中的病态问题。该算法也可同时恢复因光谱有限带宽、象差等引起的图象降质。
The Restoration of the “Double peak”in
OCT Images Based on Inverse Wiener
, http://www.100md.com
Xiang Jiying Wu Zhen Zeng Shaoqiun Luo Qingming Zhang Ping Huang Dexiu
Dept. of Optoelectronic Engineering,Huazhong University
of Science and Technology,Wuhan China
ABSTRACT It has been found that the high reflectivity film of the reference mirror in OCT may cause a socalled “double peak effect” in the result images.To eliminate this a restoration algorithm is proposed here. The method is based on the mathematical modals of the point-spread function of OCT with consideration of double peak effect. The power spectrum of the noise and signal are estimated by the average smooth periodogram method. An inverse wiener filter algorithm, which avoids the illness condition in common inverse filter, gives the final restored images.The algorithm is also capable of the image degrading recovery due to the aberration and the band -limited spectrum.
, 百拇医药
KEY WORDS Low coherence tomography Wiener filter Fourier convert Point-spread function
光学弱相干层析(OCT)[1]是一种新兴的扫描成像技术,它为临床医学提供了一种新颖的非介入式活体检测手段。虽然从提出至今只有短短几年,但已表现出极诱人应用前景。目前它已在视网膜及黄斑疾病的早期诊断,皮肤、肠、胚胎检测等领域发挥出巨大的作用[2]。被权威人士公认为它是显微领域发展的一大趋势[3]。
在国家自然科学基金的资助下,我们成功地研制出一套OCT实验装置,其纵向分辨率达10.7μm,锁相相关解调器的应用使其具有极强的抗噪声能力。然而在研制过程中发现,OCT图象质量受到“双峰值效应”的严重影响。图1为一幅盖玻片的实测OCT图象,图中两条亮线分别对应于盖玻片上下端面的反射信号,其左侧分别有两条与之平行的暗线相伴,这就是OCT图象中的双峰值效应。这种效应在图2的截断面灰度分布图中显得更为清晰。
, http://www.100md.com
在排除了由多次反射、元件的回波、及解调器引入的可能性之后,我们确认双峰效应源于参考反射镜的介质高反膜。由于高反膜的厚度大于光源的相干长度,一部分光与信号光相干,从而在输出图象中产生副峰。为消除这一效应,我们通过建立相应的数字模型研究了图象复原的算法。该算法也可同时恢复因光谱有限带宽、象差等引起的图象降质。
图1 OCT图象中的双峰值效应
图2 OCT图象截断面灰度分布
1 OCT图象降质数学模型及维纳逆滤波恢复算法
图象的降质过程可用点扩展函数来描述。首先分析z方向上一维的情景。设点扩展函数为h(z),真实图象为f(z),采样过程中受到噪声n(z)的干扰。由线性系统理论,实测图象g(z)可写为:
, 百拇医药
g(z)=f(z) h(z)+n(z)(1)
h(z)+n(z)(1)
其中 表示z方向上的卷积运算。对上式作傅里叶变换得:
表示z方向上的卷积运算。对上式作傅里叶变换得:
G(u)=F(u)H(u)+N(u)(2)
其中u为z方向上的空间频率。H(u)为系统传递函数。上式表明,欲得到真实图象f(z)的估计值f'(z),可先用逆滤波求得其频谱:
F'(u)=G(u)/H(u)
再将其作傅里叶逆变换即可得f'(z)。然而,在实际恢复过程中,逆滤波运算往往是病态的。例如,当考虑噪声[4]的影响后,有:
, http://www.100md.com
F’(u)=F(u)+N(u)/H(u)(4)
其中N(u)为噪声频谱。在一般情况下,H(u)总量随离开原点距离的变远而急剧下降,而噪声项则相对下降缓慢。因此在高频段,噪声影响将占据主导地位,甚至使恢复后的图象面目全非。因此逆滤波算法只适用于信噪比较高的图象。
如果将f和n都看作是随机信号,且其一阶矩、二阶矩都已知,则可用统计的方法估算f'的统计参数。其中一种是最小方差估计,即维纳滤波。它要求f'(z)与f(z)的均方差E{[f(z)-f'(z)]2}最小。维纳滤波器的传递函数为:
P(u)=H*(u)/[|H(u)|2+Sn(u)/Sf(u)](5)
其中Sn(u)和Sf(u)分别为噪声与信号的功率谱。当不存在噪声时,Sn(u)=0,维纳滤波器等同于逆滤波器,当有噪声时,维纳滤波器将用信噪比对恢复过程进行修正,信噪比很小时,P(u)也很小,使恢复图象较小地依赖于降质图象。若Sf(u)趋近于0,则有P(u)趋近于0,相应的F'(u)也趋近于0,这显然是合理的。在H(u)很小或等于0时,P(u)的分母始终不可能为0,因此维纳滤波没有病态问题。
, http://www.100md.com
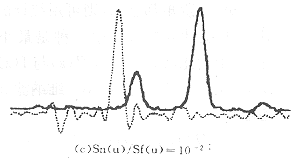
图3给出了一组纸张的OCT信号在不同的Sn(u)/Sf(u)取值下的恢复结果。由图可见,恢复之后原信号中的双峰值响应得到了抑制,脉冲宽度变窄,表明分辨率得到改善。但当Sn(u)/Sf(u)较小时恢复图象受噪声的影响很大,恢复之后的信噪比严重下降。这是因为Sn(u)/Sf(u)值较小时,维纳滤波更趋近于病态的逆滤波过程。而随着Sn(u)/Sf(u)值的增大,这一状况得到了明显的改观。
1.1 OCT点扩展函数估算
在同步扫描OCT系统中(信号臂光路与参考反射镜同步扫描),其成象特性具有空间线性不变性,而在离焦扫描OCT系统中(信号臂固定,参考镜振动),在扫描范围不大及物镜焦距较长的情况下仍可被近似看作空间不变系统,其有效点扩展函数可写为:


, 百拇医药
图3 维纳逆滤波恢复前后的信号对比(纵向点间距0.75mm)
h(x,y,z)=|g(x,y,z).Γ(2z/c)|(6)
其中g(x,y,z)为单模光纤相干共焦冲激响应,Γ(t)为光源的自相关函数。若只考虑z方向一维的情况,则有:
h(z)=|Γ(2z/c)|(7)
设光源具有高斯分布,将其光谱中心搬移到0,则其功率谱分布可写为:
S(V)=(1/Δv)(ln2/π)1/2exp[-v2ln2/Δv2]
由统计光学知光源的自相干函数Γ与其功率谱密度构成傅里叶变换对,即:
, 百拇医药
Γ(τ)=∫S(V)exp(i2πvτ)dv(9)
因此:
h(z)=|Γ(2z/c)|
=exp[-4π2Δλ2z2/λ4ln2](10)
OCT图象的双峰值效应也可用点扩展函数来描述。考虑了双峰效应的点扩展函数可写为:
h(z)=ρdp*exp[-4π2Δλ2(z+ddp)2/λ4ln2]
+exp[-4π2Δλ2z2/λ4ln2](11)
, 百拇医药
其中ρdp为副峰与主峰的高度之比,ddp为主副峰之距。在我们所设计的系统中,Δλ≈50nm,λ=1310nm,ρdp≈0.36,ddp≈37μm,相应的点扩展函数如图4所示。
1.2 功率谱估算
图4 点扩展函数
维纳滤波是一种先验算法,需要事先知道信号功率谱和噪声功率谱。假设系统中只存在白噪声,且景物信号与噪声是统计独立的,则可用变质图象功率谱中高频段作为噪声功率谱,而用低频段作为景物的功率谱。然而,OCT图象并不满足以上两项假设。首先,OCT图象是由相关解调而得,相关器已滤掉了处于多普勒频移附近的通频带以外的其它噪声,因此剩余噪声不再是白噪声,而是限带噪声。其次,即然OCT图象中噪声已通过了相关器,那么它与有用信号之间必然存在一定的关联,因此关于信号与噪声统计独立的假设也不能成立。为此,应根据实测噪声图象来估计噪声功率谱,而信号功率谱则可通过变质图象功率谱Sg(u,v)除以|H(u)|2进行估算。值得注意的是,每次改变电路参数后,都必须重新测量噪声图象。
, 百拇医药
将信号作傅里叶变换,再求其模的平方,从而得到功率谱密度(周期图法)。其定义为:
Sg(u)=|G(eiu)|2/N
其中G(eiu)为g(z)的傅里叶变换。由于对于信号g(z)只能取到有限的N点随机序列,因此周期图估计是存在偏差的,分析表明,周期图虽然是功率谱的渐近无偏估计,但却不是其一致估计。针对这一缺点,可将长度为N的序列分成K段,每段长度为L(KL=N)。计算每段周期图之前,为减少旁瓣的影响,首先对每一段乘以窗口函数W(n),称为平均平滑周期图法。第i个修正后的周期图为:
对K个周期图进行平均,得到整个信号的功率谱估计: (12)
(12)
, http://www.100md.com
这样,平均平滑周期图法就变成了一种渐近无偏的一致估计。同理,可用噪声图象来估计噪声功率谱Sn(u)。图5为一组典型的噪声波形,图6为其功率谱估计。
图5 噪声波形
图6 噪声功率谱
2 结论与讨论
维纳逆滤波算法的基本步骤为:首先采集一幅噪声图象,再用平均平滑周期图法分别计算出信号与噪声的功率谱密度函数。其次计算系统点扩展函数,并依据图象尺寸作相应的缩放。根据以上已知条件用维纳逆滤波公式求出恢复图象。

, 百拇医药
图7 维纳逆滤波恢复实例。其中图(a)(b)(e)(f)(g)(h)的纵向相邻点间距3.8μm,横向扫描点数128,图(c)(d)的纵向点间距,1.5μm,横向扫描点数128
实践证明,在OCT图象中,维纳滤器基本上都能获得较好的恢复效果。另外由于采用FFT运算[5],其速度也是令人满意的。图7给出了一组实测图象。滤波前后的图象对比可清晰地演示了维纳逆滤波算法在消除双峰值效应、改善象质中的作用。
*图家自然科学基金资助项目(基金编号39570678)
参 考 文 献
1.D.Huang.E.A.Swanson,et al.Optical coherence tomography,Science,1991,254:1178-1181
, 百拇医药
2.Zhongping Chen,Thomas E.Milner,et al.Noninvasive imaging of in vivo blood flow velocity using optical Doppler tomography,Optics Letters ,1997,22(14):1119-1121
3.S.R. Chinn and E.A.Swanson,Optical coherence tomography using a frequency-tunable optical source, Optics letters ,1997,22(5):340-342
4.J.M.Schmitt, Model of optical coherence tomography of heterogeneous tissue,J.Opt.Soc.Am.A,1997,14(6):1231-121242
5.向际鹰等.基于FFT的三维扫描图象深层损耗快速恢复方案.中国激光.1998,A25(10)
(1998年10月14日收稿), 百拇医药
单位:华中理工大学光电子系 (430074)
关键词:弱相干层析技术;维纳滤波;傅里叶变换;点扩展函数
中国医疗器械杂志990202 提要 分析了OCT系统中严重影响象质的“双峰值效应”,指出其起源为参考反射镜的介质高反膜,并通过建立相应的数学模型研究了其恢复的算法。从理论上推导了考虑双峰值效应后的OCT系统点扩展函数。用平均平滑周期图法分别估算出信号与噪声的功率谱密度函数。最后用维纳逆滤波算法得到恢复图象,避免了普通逆滤波中的病态问题。该算法也可同时恢复因光谱有限带宽、象差等引起的图象降质。
The Restoration of the “Double peak”in
OCT Images Based on Inverse Wiener
, http://www.100md.com
Xiang Jiying Wu Zhen Zeng Shaoqiun Luo Qingming Zhang Ping Huang Dexiu
Dept. of Optoelectronic Engineering,Huazhong University
of Science and Technology,Wuhan China
ABSTRACT It has been found that the high reflectivity film of the reference mirror in OCT may cause a socalled “double peak effect” in the result images.To eliminate this a restoration algorithm is proposed here. The method is based on the mathematical modals of the point-spread function of OCT with consideration of double peak effect. The power spectrum of the noise and signal are estimated by the average smooth periodogram method. An inverse wiener filter algorithm, which avoids the illness condition in common inverse filter, gives the final restored images.The algorithm is also capable of the image degrading recovery due to the aberration and the band -limited spectrum.
, 百拇医药
KEY WORDS Low coherence tomography Wiener filter Fourier convert Point-spread function
光学弱相干层析(OCT)[1]是一种新兴的扫描成像技术,它为临床医学提供了一种新颖的非介入式活体检测手段。虽然从提出至今只有短短几年,但已表现出极诱人应用前景。目前它已在视网膜及黄斑疾病的早期诊断,皮肤、肠、胚胎检测等领域发挥出巨大的作用[2]。被权威人士公认为它是显微领域发展的一大趋势[3]。
在国家自然科学基金的资助下,我们成功地研制出一套OCT实验装置,其纵向分辨率达10.7μm,锁相相关解调器的应用使其具有极强的抗噪声能力。然而在研制过程中发现,OCT图象质量受到“双峰值效应”的严重影响。图1为一幅盖玻片的实测OCT图象,图中两条亮线分别对应于盖玻片上下端面的反射信号,其左侧分别有两条与之平行的暗线相伴,这就是OCT图象中的双峰值效应。这种效应在图2的截断面灰度分布图中显得更为清晰。
, http://www.100md.com
在排除了由多次反射、元件的回波、及解调器引入的可能性之后,我们确认双峰效应源于参考反射镜的介质高反膜。由于高反膜的厚度大于光源的相干长度,一部分光与信号光相干,从而在输出图象中产生副峰。为消除这一效应,我们通过建立相应的数字模型研究了图象复原的算法。该算法也可同时恢复因光谱有限带宽、象差等引起的图象降质。

图1 OCT图象中的双峰值效应

图2 OCT图象截断面灰度分布
1 OCT图象降质数学模型及维纳逆滤波恢复算法
图象的降质过程可用点扩展函数来描述。首先分析z方向上一维的情景。设点扩展函数为h(z),真实图象为f(z),采样过程中受到噪声n(z)的干扰。由线性系统理论,实测图象g(z)可写为:
, 百拇医药
g(z)=f(z)
 h(z)+n(z)(1)
h(z)+n(z)(1)其中
 表示z方向上的卷积运算。对上式作傅里叶变换得:
表示z方向上的卷积运算。对上式作傅里叶变换得:G(u)=F(u)H(u)+N(u)(2)
其中u为z方向上的空间频率。H(u)为系统传递函数。上式表明,欲得到真实图象f(z)的估计值f'(z),可先用逆滤波求得其频谱:
F'(u)=G(u)/H(u)
再将其作傅里叶逆变换即可得f'(z)。然而,在实际恢复过程中,逆滤波运算往往是病态的。例如,当考虑噪声[4]的影响后,有:
, http://www.100md.com
F’(u)=F(u)+N(u)/H(u)(4)
其中N(u)为噪声频谱。在一般情况下,H(u)总量随离开原点距离的变远而急剧下降,而噪声项则相对下降缓慢。因此在高频段,噪声影响将占据主导地位,甚至使恢复后的图象面目全非。因此逆滤波算法只适用于信噪比较高的图象。
如果将f和n都看作是随机信号,且其一阶矩、二阶矩都已知,则可用统计的方法估算f'的统计参数。其中一种是最小方差估计,即维纳滤波。它要求f'(z)与f(z)的均方差E{[f(z)-f'(z)]2}最小。维纳滤波器的传递函数为:
P(u)=H*(u)/[|H(u)|2+Sn(u)/Sf(u)](5)
其中Sn(u)和Sf(u)分别为噪声与信号的功率谱。当不存在噪声时,Sn(u)=0,维纳滤波器等同于逆滤波器,当有噪声时,维纳滤波器将用信噪比对恢复过程进行修正,信噪比很小时,P(u)也很小,使恢复图象较小地依赖于降质图象。若Sf(u)趋近于0,则有P(u)趋近于0,相应的F'(u)也趋近于0,这显然是合理的。在H(u)很小或等于0时,P(u)的分母始终不可能为0,因此维纳滤波没有病态问题。
, http://www.100md.com
图3给出了一组纸张的OCT信号在不同的Sn(u)/Sf(u)取值下的恢复结果。由图可见,恢复之后原信号中的双峰值响应得到了抑制,脉冲宽度变窄,表明分辨率得到改善。但当Sn(u)/Sf(u)较小时恢复图象受噪声的影响很大,恢复之后的信噪比严重下降。这是因为Sn(u)/Sf(u)值较小时,维纳滤波更趋近于病态的逆滤波过程。而随着Sn(u)/Sf(u)值的增大,这一状况得到了明显的改观。
1.1 OCT点扩展函数估算
在同步扫描OCT系统中(信号臂光路与参考反射镜同步扫描),其成象特性具有空间线性不变性,而在离焦扫描OCT系统中(信号臂固定,参考镜振动),在扫描范围不大及物镜焦距较长的情况下仍可被近似看作空间不变系统,其有效点扩展函数可写为:




, 百拇医药
图3 维纳逆滤波恢复前后的信号对比(纵向点间距0.75mm)
h(x,y,z)=|g(x,y,z).Γ(2z/c)|(6)
其中g(x,y,z)为单模光纤相干共焦冲激响应,Γ(t)为光源的自相关函数。若只考虑z方向一维的情况,则有:
h(z)=|Γ(2z/c)|(7)
设光源具有高斯分布,将其光谱中心搬移到0,则其功率谱分布可写为:
S(V)=(1/Δv)(ln2/π)1/2exp[-v2ln2/Δv2]
由统计光学知光源的自相干函数Γ与其功率谱密度构成傅里叶变换对,即:
, 百拇医药
Γ(τ)=∫S(V)exp(i2πvτ)dv(9)
因此:
h(z)=|Γ(2z/c)|
=exp[-4π2Δλ2z2/λ4ln2](10)
OCT图象的双峰值效应也可用点扩展函数来描述。考虑了双峰效应的点扩展函数可写为:
h(z)=ρdp*exp[-4π2Δλ2(z+ddp)2/λ4ln2]
+exp[-4π2Δλ2z2/λ4ln2](11)
, 百拇医药
其中ρdp为副峰与主峰的高度之比,ddp为主副峰之距。在我们所设计的系统中,Δλ≈50nm,λ=1310nm,ρdp≈0.36,ddp≈37μm,相应的点扩展函数如图4所示。
1.2 功率谱估算

图4 点扩展函数
维纳滤波是一种先验算法,需要事先知道信号功率谱和噪声功率谱。假设系统中只存在白噪声,且景物信号与噪声是统计独立的,则可用变质图象功率谱中高频段作为噪声功率谱,而用低频段作为景物的功率谱。然而,OCT图象并不满足以上两项假设。首先,OCT图象是由相关解调而得,相关器已滤掉了处于多普勒频移附近的通频带以外的其它噪声,因此剩余噪声不再是白噪声,而是限带噪声。其次,即然OCT图象中噪声已通过了相关器,那么它与有用信号之间必然存在一定的关联,因此关于信号与噪声统计独立的假设也不能成立。为此,应根据实测噪声图象来估计噪声功率谱,而信号功率谱则可通过变质图象功率谱Sg(u,v)除以|H(u)|2进行估算。值得注意的是,每次改变电路参数后,都必须重新测量噪声图象。
, 百拇医药
将信号作傅里叶变换,再求其模的平方,从而得到功率谱密度(周期图法)。其定义为:
Sg(u)=|G(eiu)|2/N
其中G(eiu)为g(z)的傅里叶变换。由于对于信号g(z)只能取到有限的N点随机序列,因此周期图估计是存在偏差的,分析表明,周期图虽然是功率谱的渐近无偏估计,但却不是其一致估计。针对这一缺点,可将长度为N的序列分成K段,每段长度为L(KL=N)。计算每段周期图之前,为减少旁瓣的影响,首先对每一段乘以窗口函数W(n),称为平均平滑周期图法。第i个修正后的周期图为:

对K个周期图进行平均,得到整个信号的功率谱估计:
 (12)
(12), http://www.100md.com
这样,平均平滑周期图法就变成了一种渐近无偏的一致估计。同理,可用噪声图象来估计噪声功率谱Sn(u)。图5为一组典型的噪声波形,图6为其功率谱估计。

图5 噪声波形

图6 噪声功率谱
2 结论与讨论
维纳逆滤波算法的基本步骤为:首先采集一幅噪声图象,再用平均平滑周期图法分别计算出信号与噪声的功率谱密度函数。其次计算系统点扩展函数,并依据图象尺寸作相应的缩放。根据以上已知条件用维纳逆滤波公式求出恢复图象。


, 百拇医药
图7 维纳逆滤波恢复实例。其中图(a)(b)(e)(f)(g)(h)的纵向相邻点间距3.8μm,横向扫描点数128,图(c)(d)的纵向点间距,1.5μm,横向扫描点数128
实践证明,在OCT图象中,维纳滤器基本上都能获得较好的恢复效果。另外由于采用FFT运算[5],其速度也是令人满意的。图7给出了一组实测图象。滤波前后的图象对比可清晰地演示了维纳逆滤波算法在消除双峰值效应、改善象质中的作用。
*图家自然科学基金资助项目(基金编号39570678)
参 考 文 献
1.D.Huang.E.A.Swanson,et al.Optical coherence tomography,Science,1991,254:1178-1181
, 百拇医药
2.Zhongping Chen,Thomas E.Milner,et al.Noninvasive imaging of in vivo blood flow velocity using optical Doppler tomography,Optics Letters ,1997,22(14):1119-1121
3.S.R. Chinn and E.A.Swanson,Optical coherence tomography using a frequency-tunable optical source, Optics letters ,1997,22(5):340-342
4.J.M.Schmitt, Model of optical coherence tomography of heterogeneous tissue,J.Opt.Soc.Am.A,1997,14(6):1231-121242
5.向际鹰等.基于FFT的三维扫描图象深层损耗快速恢复方案.中国激光.1998,A25(10)
(1998年10月14日收稿), 百拇医药