基于小波变换的甲襞微循环图像边缘检测*
作者:郑慧如 方明
单位:福州大学 (350002)
关键词:甲襞微循环;小波变换;图像处理
中国医疗器械杂志990305 提要 讨论了小波变换在图像边缘检测、分类与描述中的作用,并根据甲襞微循环图像的特点,利用三次样条二进小波,采用Mallat快速算法进行小波分解,成功地提取了甲襞微循环图像的边缘。
The Nail Fold Micro-Circulation Images Edges
Detection Based on Wavelet Transform
Zheng Huiru Fang ming
Fuzhou University
, 百拇医药
ABSTRACT In this paper, we discuss the application of wavelet transform to edges detection, classification and description. Then, according to the peculiarity of the nail fold micro-circulation images, dyadic wavelet transform is successfully applied to detect the edges and the Mallat algorithm is used in the wavelet decomposition
KEY WORDS Nail Fold Micro-Circulation Wavelet Rtansform Image Processing
甲襞微循环图像各参数的测量是心血管疾病无损检测的一种重要手段,其图像边缘的准确提取是自动检测微循环各参数的基础。但甲襞微循环图像为反光式图像,信号噪声大,明暗对比度较差,灰阶分布范围小,一般在90~150之间;由于图像中边缘和噪声在空域上均表现为有较大的灰阶差,在时域上则均为高频分量,给检测带来困难。其中,采用传统的梯度法和灰度法会带来较多的误测和漏测,效果不能令人满意,而改进的自适应阈值模板相关匹配算法[1],虽然能较好克服误测和漏测,但仍存在一些不足:即检测出的边缘会出现较多的断缺,需要插值光滑,且微循环图像顶部弯曲部分边缘不能检测出来,为图像的晃动纠正等带来困难。同时在模板的实际选择中也有一个权衡问题:小尺度的边缘模板,对噪声很敏感,定位精度高;大尺度的边缘模板,有较强的去噪声能力,但定位精度低。只有采用多尺度的方法才能使高定位精度及强去噪能力两者统一起来。小波变换正好具有良好的空间局部分析功能和多尺度多分辨分析功能,为此,本文试将小波变换用于甲襞微循环图像的边缘检测,克服了上述不足,取得了较好的结果。
, http://www.100md.com
1 原理和方法
1.1 连续小波及二进小波的定义和小波变换的性质[2][3][4]
定义1 设Ψ∈L1∩L2,是一个能量有限的函数,则按如下方式生成函数族{Ψa,b}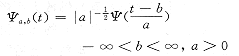
式中Ψ(t)称为小波母函数(Mother Wavelet),Ψa,b(t)是通过母函数Ψ(t)的展缩和位移生成的。称为小波基函数或连续小波或分析小波(Analyzing Wavelet),a为尺度参数,b为位置参数,其中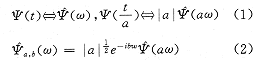
小波母函数必须满足以下允许条件(Admissible Condition)及稳定性条件(Stability Condition),若存在二常数0
, http://www.100md.com
任一连续的一维时域信号f(t)的连续小波变换定义为该信号和小波基函数的内积(采用卷积):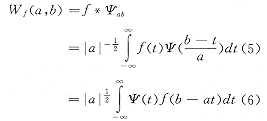
一维时域二进尺度的离散小波变换,简称为二进小波变换,DWf(j,n)的定义如下:
设
t=k(Δt),b=n(Δt),a=2j(j∈Z) (7)
(7)
定义2 二维空域二进尺度的离散小波变换:
设空域信号为f(x,y),离散量化为f(k1,k2),相应小波基为[Ψ(k1),Ψ2(k2)],二进尺度参数a=2j,则定义
, 百拇医药
W2jf(x,y)=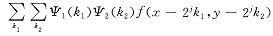
设H(ω),G(ω)分别为低、高通滤波器,可选作为母函数Ψ(ω)构造二进小波。本文选用三次样条函数,即: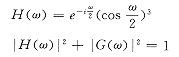
这时,hn=h1-n,gn=-g1-n
hn与gn的数值如下:
(当n>3时,hn=gn=0)
h1=0.3750, h2=0.1250, h3=0
, http://www.100md.com
g1=0.5798, g2=0.0869, g3=0.0061
可见,三次样条小波具有如下性质:
(1)它是一个对称小波,不会产生时间(或空间)的偏移,这是进行边缘检测的前提。
(2)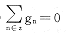 即为高通滤波器,这是可用于边缘检测的基础。
即为高通滤波器,这是可用于边缘检测的基础。
1.2 检测算法
为提高速度,本文采用二维小波变换的Mallat快速算法[5],进行小波分解。
Mallat算法的二维形式为: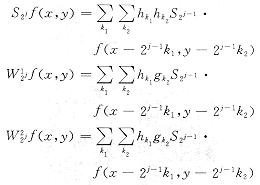
, 百拇医药
其中,S20f(x,y)=f(x,y),f(x,y)是原始的二维数字信号,S2jf(x,y)是f(x,y)在分辨j下的离散概貌,W12jf(x,y)是f(x,y)在分辨率j下沿垂直方向的离散细节,W22jf(x,y)是在分辨率j下沿水平方向的离散细节。
考察图像边缘的特性,可知:二维信号的急剧变化范围通常不是某单个孤立点而是图像所在平面中的一条曲线,沿着这些曲线,在一个方向上是奇异的,而在其垂直方向却是平滑的,而这条曲线正对应着多尺度小波变换模的局部极大值,因此,可通过寻找图像在不同尺度下小波变换模局部极大值点,进而形成极值链,来检测图像的边缘[4]。
本文采用的检测算法流程为:
, 百拇医药
Step1.选择分解尺度J和模阀值ε
Step2.对f(x,y)进行递增j值小波变换,0++,得到:
{W121f(x,y),W221f(x,y)},{W122f(x,y),W222f(x,y)}…{W12jf(x,y),W21jf(x,y)}
Step3. 计算模值M2jf(x,y)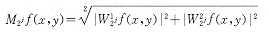
, 百拇医药
Step4. 对阈值进行处理。
若|M2if(x,y)|>ε,则置边缘线f'(x,y)=200。否则,边缘线f'(x,y)=0
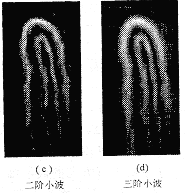
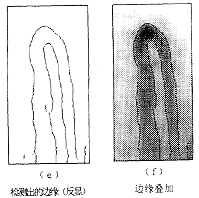
图1 甲襞微特循环图像的小波变换
2.实验与结果
本文采用上述算法对甲襞微循环图像进行边缘检测,如图所示。图(a)为原始图像,对于甲襞微循环图象,其图象灰度变化较小,图(b)~(d)分别为图象的一阶、二阶、三阶小波变换,经小波变换后,得到的边缘带较宽,经过算法的细化后即可求出血管边缘。从图(f)可见,检测出的边缘与实际边缘吻合得很好,并且边缘的连续性也较好,很少出现断线,弯曲部分边缘能准确提取,可用于序列图像的边缘晃动校正。用小波变换方法,基本可克服前述方法的不足,能较好地提取出边缘信息。
, http://www.100md.com
3.分析讨论
理论分析与实验证明,小波变换可为医学图像如甲襞微循环图像等的边缘检测提供一种有效的新方法,具有计算复杂度低,速度快等优点。但实际使用时,应视原始图像的特点选择合适的小波母函数进行,笔者曾用Harr小波进行边缘提取,但不适用于甲襞微循环图像。有关小波函数的选择、构造问题还将进行更深入的研究。
*福建省自然科学基金资助项目
参 考 文 献
1 郑慧如.一种甲襞微循环图象处理的新算法.生物医学工程前沿.中国出版社.1993,89-92
2 J.Canny.A Computational approach to edgr detection IEEE Trans.On Pattern Analysis and Machine Intelligence.1986,Vol.8,pp.679-698
3 D.Marr and E.HILDRETH.Theory of edge detection,Proc.of the Royal Society of London.1980;Vol.207.187-217
4 秦前清等.实用小波分析,西安电子科技大学出版社.1995;15-75
5 刘景忠等.小波分析及其应用.西安电子科技大学出版社.1995;30-36
(1998年8月18日收稿), http://www.100md.com
单位:福州大学 (350002)
关键词:甲襞微循环;小波变换;图像处理
中国医疗器械杂志990305 提要 讨论了小波变换在图像边缘检测、分类与描述中的作用,并根据甲襞微循环图像的特点,利用三次样条二进小波,采用Mallat快速算法进行小波分解,成功地提取了甲襞微循环图像的边缘。
The Nail Fold Micro-Circulation Images Edges
Detection Based on Wavelet Transform
Zheng Huiru Fang ming
Fuzhou University
, 百拇医药
ABSTRACT In this paper, we discuss the application of wavelet transform to edges detection, classification and description. Then, according to the peculiarity of the nail fold micro-circulation images, dyadic wavelet transform is successfully applied to detect the edges and the Mallat algorithm is used in the wavelet decomposition
KEY WORDS Nail Fold Micro-Circulation Wavelet Rtansform Image Processing
甲襞微循环图像各参数的测量是心血管疾病无损检测的一种重要手段,其图像边缘的准确提取是自动检测微循环各参数的基础。但甲襞微循环图像为反光式图像,信号噪声大,明暗对比度较差,灰阶分布范围小,一般在90~150之间;由于图像中边缘和噪声在空域上均表现为有较大的灰阶差,在时域上则均为高频分量,给检测带来困难。其中,采用传统的梯度法和灰度法会带来较多的误测和漏测,效果不能令人满意,而改进的自适应阈值模板相关匹配算法[1],虽然能较好克服误测和漏测,但仍存在一些不足:即检测出的边缘会出现较多的断缺,需要插值光滑,且微循环图像顶部弯曲部分边缘不能检测出来,为图像的晃动纠正等带来困难。同时在模板的实际选择中也有一个权衡问题:小尺度的边缘模板,对噪声很敏感,定位精度高;大尺度的边缘模板,有较强的去噪声能力,但定位精度低。只有采用多尺度的方法才能使高定位精度及强去噪能力两者统一起来。小波变换正好具有良好的空间局部分析功能和多尺度多分辨分析功能,为此,本文试将小波变换用于甲襞微循环图像的边缘检测,克服了上述不足,取得了较好的结果。
, http://www.100md.com
1 原理和方法
1.1 连续小波及二进小波的定义和小波变换的性质[2][3][4]
定义1 设Ψ∈L1∩L2,是一个能量有限的函数,则按如下方式生成函数族{Ψa,b}
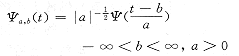
式中Ψ(t)称为小波母函数(Mother Wavelet),Ψa,b(t)是通过母函数Ψ(t)的展缩和位移生成的。称为小波基函数或连续小波或分析小波(Analyzing Wavelet),a为尺度参数,b为位置参数,其中
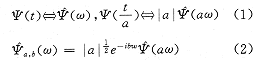
小波母函数必须满足以下允许条件(Admissible Condition)及稳定性条件(Stability Condition),若存在二常数0
, http://www.100md.com
任一连续的一维时域信号f(t)的连续小波变换定义为该信号和小波基函数的内积(采用卷积):
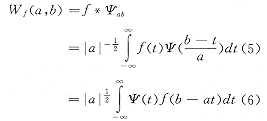
一维时域二进尺度的离散小波变换,简称为二进小波变换,DWf(j,n)的定义如下:
设
t=k(Δt),b=n(Δt),a=2j(j∈Z)
 (7)
(7)定义2 二维空域二进尺度的离散小波变换:
设空域信号为f(x,y),离散量化为f(k1,k2),相应小波基为[Ψ(k1),Ψ2(k2)],二进尺度参数a=2j,则定义
, 百拇医药
W2jf(x,y)=
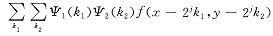
设H(ω),G(ω)分别为低、高通滤波器,可选作为母函数Ψ(ω)构造二进小波。本文选用三次样条函数,即:
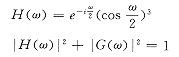
这时,hn=h1-n,gn=-g1-n
hn与gn的数值如下:
(当n>3时,hn=gn=0)
h1=0.3750, h2=0.1250, h3=0
, http://www.100md.com
g1=0.5798, g2=0.0869, g3=0.0061
可见,三次样条小波具有如下性质:
(1)它是一个对称小波,不会产生时间(或空间)的偏移,这是进行边缘检测的前提。
(2)
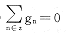 即为高通滤波器,这是可用于边缘检测的基础。
即为高通滤波器,这是可用于边缘检测的基础。1.2 检测算法
为提高速度,本文采用二维小波变换的Mallat快速算法[5],进行小波分解。
Mallat算法的二维形式为:
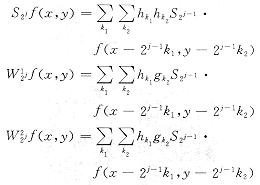
, 百拇医药
其中,S20f(x,y)=f(x,y),f(x,y)是原始的二维数字信号,S2jf(x,y)是f(x,y)在分辨j下的离散概貌,W12jf(x,y)是f(x,y)在分辨率j下沿垂直方向的离散细节,W22jf(x,y)是在分辨率j下沿水平方向的离散细节。
考察图像边缘的特性,可知:二维信号的急剧变化范围通常不是某单个孤立点而是图像所在平面中的一条曲线,沿着这些曲线,在一个方向上是奇异的,而在其垂直方向却是平滑的,而这条曲线正对应着多尺度小波变换模的局部极大值,因此,可通过寻找图像在不同尺度下小波变换模局部极大值点,进而形成极值链,来检测图像的边缘[4]。
本文采用的检测算法流程为:
, 百拇医药
Step1.选择分解尺度J和模阀值ε
Step2.对f(x,y)进行递增j值小波变换,0
{W121f(x,y),W221f(x,y)},{W122f(x,y),W222f(x,y)}…{W12jf(x,y),W21jf(x,y)}
Step3. 计算模值M2jf(x,y)
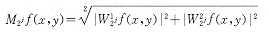
, 百拇医药
Step4. 对阈值进行处理。
若|M2if(x,y)|>ε,则置边缘线f'(x,y)=200。否则,边缘线f'(x,y)=0



图1 甲襞微特循环图像的小波变换
2.实验与结果
本文采用上述算法对甲襞微循环图像进行边缘检测,如图所示。图(a)为原始图像,对于甲襞微循环图象,其图象灰度变化较小,图(b)~(d)分别为图象的一阶、二阶、三阶小波变换,经小波变换后,得到的边缘带较宽,经过算法的细化后即可求出血管边缘。从图(f)可见,检测出的边缘与实际边缘吻合得很好,并且边缘的连续性也较好,很少出现断线,弯曲部分边缘能准确提取,可用于序列图像的边缘晃动校正。用小波变换方法,基本可克服前述方法的不足,能较好地提取出边缘信息。
, http://www.100md.com
3.分析讨论
理论分析与实验证明,小波变换可为医学图像如甲襞微循环图像等的边缘检测提供一种有效的新方法,具有计算复杂度低,速度快等优点。但实际使用时,应视原始图像的特点选择合适的小波母函数进行,笔者曾用Harr小波进行边缘提取,但不适用于甲襞微循环图像。有关小波函数的选择、构造问题还将进行更深入的研究。
*福建省自然科学基金资助项目
参 考 文 献
1 郑慧如.一种甲襞微循环图象处理的新算法.生物医学工程前沿.中国出版社.1993,89-92
2 J.Canny.A Computational approach to edgr detection IEEE Trans.On Pattern Analysis and Machine Intelligence.1986,Vol.8,pp.679-698
3 D.Marr and E.HILDRETH.Theory of edge detection,Proc.of the Royal Society of London.1980;Vol.207.187-217
4 秦前清等.实用小波分析,西安电子科技大学出版社.1995;15-75
5 刘景忠等.小波分析及其应用.西安电子科技大学出版社.1995;30-36
(1998年8月18日收稿), http://www.100md.com