相关噪声检测在脑血流信号提取中的应用
作者:吴小培 王 玮 孔 锐
单位:(安徽大学 电子工程与信息科学系,合肥 230039)
关键词:相关检测;脑血流信号;相干平均法
生物医学工程学杂志980310 内容摘要 利用相关检测原理和对脑血流信号的先验知识,应用相干平均法对含有随机噪声的脑血流信号进行噪声消除,从而恢复出原有的脑血流信号波形。文章最后给出了实测结果。
Correlation Noise Detection in Encephaloblood-fluidity Singal
Wu Xiaopei Wang Wei Kong Rui
(Dept.of Electronic Engineering and Information Science, Anhui University, Hefei 230039)
, 百拇医药
Abstract The aim of this study was to remove random white noise which mixes with encephaloblood fluidity signal.Based on the principles of correlation detection and a priori knowledge of encephaloblood fluidity,the authors adopted the coherent averaging method and obtained pure encephaloblood fluidity signal.The result of practical use has demonstrated that the more times the averaging progresses,the more distinctly the wave shows up.
Key words Correlation detection Encephaloblood fluidity Coherent averaging method
, 百拇医药
1 引 言
大部分弱生理信号都是以电信号形式出现的,如心电信号、脑电信号,肌电信号、眼电号等,然而由于随机噪声的存在很大程度上影响了弱生理信号的检测,以脑血流信号为例,它是对脑部搏动性血流供应状况和判断脑血管紧张程度、弹性及周围阻力的宏观反应。脑血流信号虽是不规则信号,但也有其自己的特点,然而由于随机噪声的干扰,使得脑血流信号的特征不易观察得到,从而造成医生的误诊。因此,对脑血流信号中随机噪声的消除就具有十分重要的实际应用价值。本文利用了相关检测技术与相干平均法对实际的脑血流信号进行相关检测,去除随机噪声,并取得了较好的效果。
2 脑血流信号
血液在体内是类似于脑脊液的良好导体,其电阻率为150 Ωcm,活体脑组织的电阻率为225 Ωcm,并且它们的导电性能比较稳定,电阻变化较小,而血液的电阻则随着心动周期的变化而变化,可近似看成为一个周期信号。因此在血管上加一个适当的电源,就可以把脑血流变化情况变为形象的电信号波形。它可以比较客观地估计出头部的血流动力学改变情况,后经过检波,放大处理所描记的图形就是阻抗式脑血流图。
, http://www.100md.com
这种阻抗式脑血流图的一般典型波形及参数如图所示。图1是脑血流信号波形的纵轴参数,图2是脑血流信号波形的横轴参数。
图1中,h1代表波幅,h2代表切迹高,h3代表重搏波波幅。h4代表切迹深。图2中,t1表示上升时间,t2表示峰峰时间,t3表示重搏波波后时间,t1+t2+t3即为脑血流信号的周期。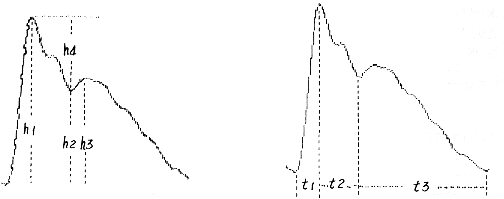
图1 纵轴参数 图2 横轴参数
Fig 1 Hovizontal parameters Fig 2 Vertical parameters
, http://www.100md.com
其中用于病理诊断依据的参数有:上升时间,波幅值,两侧波幅差,重搏波等。医生可根据不同的参数值诊断某人的脑血流信号是否正常。
3 相干平均法及应用
通常当对某一器官进行刺激时所记录的诱发响应X(k)由两部分组成,即真实信号S(k)与噪声信号n(k)
X(k)=S(k)+n(k)(1)
相干平均法是指多次重复刺激——响应实验,并记录每一次的结果
Xi(k)=Si(k)+ni(k) i=0,…,M-1(2)
其中:i为刺激的序号;M为刺激的总次数。Xi(k)的特点是其中的真实信号部分Si(k)的一些特征往往被噪声淹没。考虑到S(k)既然反映了生物体的某种特征,在刺激的客观条件不变的情况下,每次的Si(k)应保持不变,即So(k)=S1(k)=…=SM-1(k)=S(k)。假设噪声n(k)是零均值、方差为σ2的平稳随机信号,且对每一次刺激,它们是不相关的,即:
, http://www.100md.com
E[ni(k)nj(k)]=0, i≠j(3)
若记信号的功率为P,则X(k)的信噪比为
SNR0=P/σ2(4)
现对X(k)的M次样本起点对齐后相加并平均,则结果为:
可见经M次平均后信号的功率仍为P,噪声的均值仍为零,但噪声方差为σ2/M,因此相加平均后的信噪比为:
SNR1=P2/σ2/M=M*P2/σ2=M*SNR0(6)
, 百拇医药
可见信噪比提高了M倍,且平均次数越多,效果越好。
对于脑血流信号,由于存着明显的周期性,因此在一次脑血流信号的采集过程中,可以得到多个周期的脑血流波形。每一个周期内包含一个完整的真实脑血流波形和随机噪声。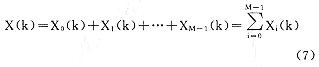
其中
Xi(k)=Si(k)+ni(k),iN≤k<(i+1)N,i=0,…,M-1(8)
N为一个周期的采样点数。
由于一个周期的脑血流波形包含了所需的全部特征参数,因此(7)式中的Xi(k)(一次刺激所得的脑血流信号的一个周期)与(2)式中的Xi(k)是等价的。因此同样可利用相干平均法消除随机噪声。即把各个周期的起点对齐后,相加平均,得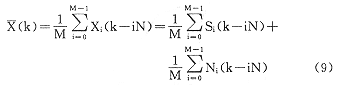
, 百拇医药
基于同样的假设,即
S0(k)=S1(k-N)=S2(k-2N)=…=SM-1(k-(M-1)N)=S(k)(10)
E[ni(k-iN)nj(k-jN)]=0,i≠j,i、j=0,…,M-1(11)
得
显然信噪比提高M倍。
在实际处理过程中,考虑到被测试者受外界环境的影响和刺激,可能会造成不同周期中Si(k)的波形有所差别,这样会造成起点对齐困难。因此当信号X(k)被存入计算机后,可从X(k)中提取一个较为典型的周期作为模板,利用相关检测法取与模板相似程度较高的其它周期,然后再进行相干平均,这样在很大程度上提高了计算精度。
, http://www.100md.com
4 实验结果
我们在基于微机的脑血流信号分析系统上进行了实验,图3是含有随机噪声的脑血流信号,在随机噪声的干扰下,波形中的很多重要特征(如重搏波等)都难以观察。图4是相加平均15次后的去噪波形。图5是相加平均150次后去噪波形。可见随着累加次数的增加,波形的特征越来越清晰,噪声消除效果很理想。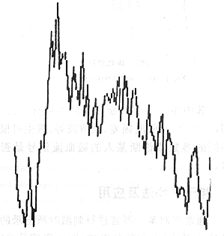
图3 含有随机噪声的信号
Fig 3 Signal with random noise
图4 平均15次后的信号
图5 平均150次后的信号
, 百拇医药
Fig 4 Signal averaged 15 times
Fig 5 Signal averaged 150 times
5 结束语
本文通过对实际人体脑血流信号的检测,应用相干平均法对含有随机噪声的信号进行了噪声消除,实测效果较好,说明此方法是可行的。但是所需的累加次数愈多,需要的时间也愈长,使得平稳假设难以保证,因此如何减少提取信号所需的累加次数,则有待进一步研究。
参 考 文 献
1 杨福生,高上凯.生物医学信号处理.北京:高等教育出版社,1989
2 戴逸松.微弱信号检测方法及仪器,北京:国防工业出版
社,1994
3 谢正祥等,医学信号数字处理技术及应用 北京:科学技术文献出版社,1992
4 孔祥勤,俞昌正.临床脑电阻图.山东:山东科技出版社
(收稿:1997-02-24 修回1997-06-02), 百拇医药
单位:(安徽大学 电子工程与信息科学系,合肥 230039)
关键词:相关检测;脑血流信号;相干平均法
生物医学工程学杂志980310 内容摘要 利用相关检测原理和对脑血流信号的先验知识,应用相干平均法对含有随机噪声的脑血流信号进行噪声消除,从而恢复出原有的脑血流信号波形。文章最后给出了实测结果。
Correlation Noise Detection in Encephaloblood-fluidity Singal
Wu Xiaopei Wang Wei Kong Rui
(Dept.of Electronic Engineering and Information Science, Anhui University, Hefei 230039)
, 百拇医药
Abstract The aim of this study was to remove random white noise which mixes with encephaloblood fluidity signal.Based on the principles of correlation detection and a priori knowledge of encephaloblood fluidity,the authors adopted the coherent averaging method and obtained pure encephaloblood fluidity signal.The result of practical use has demonstrated that the more times the averaging progresses,the more distinctly the wave shows up.
Key words Correlation detection Encephaloblood fluidity Coherent averaging method
, 百拇医药
1 引 言
大部分弱生理信号都是以电信号形式出现的,如心电信号、脑电信号,肌电信号、眼电号等,然而由于随机噪声的存在很大程度上影响了弱生理信号的检测,以脑血流信号为例,它是对脑部搏动性血流供应状况和判断脑血管紧张程度、弹性及周围阻力的宏观反应。脑血流信号虽是不规则信号,但也有其自己的特点,然而由于随机噪声的干扰,使得脑血流信号的特征不易观察得到,从而造成医生的误诊。因此,对脑血流信号中随机噪声的消除就具有十分重要的实际应用价值。本文利用了相关检测技术与相干平均法对实际的脑血流信号进行相关检测,去除随机噪声,并取得了较好的效果。
2 脑血流信号
血液在体内是类似于脑脊液的良好导体,其电阻率为150 Ωcm,活体脑组织的电阻率为225 Ωcm,并且它们的导电性能比较稳定,电阻变化较小,而血液的电阻则随着心动周期的变化而变化,可近似看成为一个周期信号。因此在血管上加一个适当的电源,就可以把脑血流变化情况变为形象的电信号波形。它可以比较客观地估计出头部的血流动力学改变情况,后经过检波,放大处理所描记的图形就是阻抗式脑血流图。
, http://www.100md.com
这种阻抗式脑血流图的一般典型波形及参数如图所示。图1是脑血流信号波形的纵轴参数,图2是脑血流信号波形的横轴参数。
图1中,h1代表波幅,h2代表切迹高,h3代表重搏波波幅。h4代表切迹深。图2中,t1表示上升时间,t2表示峰峰时间,t3表示重搏波波后时间,t1+t2+t3即为脑血流信号的周期。

图1 纵轴参数 图2 横轴参数
Fig 1 Hovizontal parameters Fig 2 Vertical parameters
, http://www.100md.com
其中用于病理诊断依据的参数有:上升时间,波幅值,两侧波幅差,重搏波等。医生可根据不同的参数值诊断某人的脑血流信号是否正常。
3 相干平均法及应用
通常当对某一器官进行刺激时所记录的诱发响应X(k)由两部分组成,即真实信号S(k)与噪声信号n(k)
X(k)=S(k)+n(k)(1)
相干平均法是指多次重复刺激——响应实验,并记录每一次的结果
Xi(k)=Si(k)+ni(k) i=0,…,M-1(2)
其中:i为刺激的序号;M为刺激的总次数。Xi(k)的特点是其中的真实信号部分Si(k)的一些特征往往被噪声淹没。考虑到S(k)既然反映了生物体的某种特征,在刺激的客观条件不变的情况下,每次的Si(k)应保持不变,即So(k)=S1(k)=…=SM-1(k)=S(k)。假设噪声n(k)是零均值、方差为σ2的平稳随机信号,且对每一次刺激,它们是不相关的,即:
, http://www.100md.com
E[ni(k)nj(k)]=0, i≠j(3)
若记信号的功率为P,则X(k)的信噪比为
SNR0=P/σ2(4)
现对X(k)的M次样本起点对齐后相加并平均,则结果为:

可见经M次平均后信号的功率仍为P,噪声的均值仍为零,但噪声方差为σ2/M,因此相加平均后的信噪比为:
SNR1=P2/σ2/M=M*P2/σ2=M*SNR0(6)
, 百拇医药
可见信噪比提高了M倍,且平均次数越多,效果越好。
对于脑血流信号,由于存着明显的周期性,因此在一次脑血流信号的采集过程中,可以得到多个周期的脑血流波形。每一个周期内包含一个完整的真实脑血流波形和随机噪声。
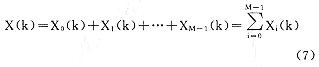
其中
Xi(k)=Si(k)+ni(k),iN≤k<(i+1)N,i=0,…,M-1(8)
N为一个周期的采样点数。
由于一个周期的脑血流波形包含了所需的全部特征参数,因此(7)式中的Xi(k)(一次刺激所得的脑血流信号的一个周期)与(2)式中的Xi(k)是等价的。因此同样可利用相干平均法消除随机噪声。即把各个周期的起点对齐后,相加平均,得
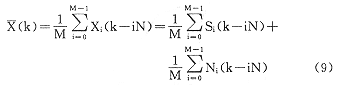
, 百拇医药
基于同样的假设,即
S0(k)=S1(k-N)=S2(k-2N)=…=SM-1(k-(M-1)N)=S(k)(10)
E[ni(k-iN)nj(k-jN)]=0,i≠j,i、j=0,…,M-1(11)
得

显然信噪比提高M倍。
在实际处理过程中,考虑到被测试者受外界环境的影响和刺激,可能会造成不同周期中Si(k)的波形有所差别,这样会造成起点对齐困难。因此当信号X(k)被存入计算机后,可从X(k)中提取一个较为典型的周期作为模板,利用相关检测法取与模板相似程度较高的其它周期,然后再进行相干平均,这样在很大程度上提高了计算精度。
, http://www.100md.com
4 实验结果
我们在基于微机的脑血流信号分析系统上进行了实验,图3是含有随机噪声的脑血流信号,在随机噪声的干扰下,波形中的很多重要特征(如重搏波等)都难以观察。图4是相加平均15次后的去噪波形。图5是相加平均150次后去噪波形。可见随着累加次数的增加,波形的特征越来越清晰,噪声消除效果很理想。

图3 含有随机噪声的信号
Fig 3 Signal with random noise

图4 平均15次后的信号
图5 平均150次后的信号
, 百拇医药
Fig 4 Signal averaged 15 times
Fig 5 Signal averaged 150 times
5 结束语
本文通过对实际人体脑血流信号的检测,应用相干平均法对含有随机噪声的信号进行了噪声消除,实测效果较好,说明此方法是可行的。但是所需的累加次数愈多,需要的时间也愈长,使得平稳假设难以保证,因此如何减少提取信号所需的累加次数,则有待进一步研究。
参 考 文 献
1 杨福生,高上凯.生物医学信号处理.北京:高等教育出版社,1989
2 戴逸松.微弱信号检测方法及仪器,北京:国防工业出版
社,1994
3 谢正祥等,医学信号数字处理技术及应用 北京:科学技术文献出版社,1992
4 孔祥勤,俞昌正.临床脑电阻图.山东:山东科技出版社
(收稿:1997-02-24 修回1997-06-02), 百拇医药