糖尿病人心率变异的李雅普洛夫指数的计算
作者:周亮飞 秦明新
单位:周亮飞 秦明新 (第四军医大学 生物医学工程系,西安 710032)
关键词:心率变异性;李雅普洛夫指数;糖尿病
生物医学工程学杂志990114 内容摘要 采用常规的李雅普洛夫指数定义的方法和长度演化法、面积演化法分别计算10例正常人和10例糖尿病人的李雅普洛夫指数,结果显示糖尿病人的李雅普洛夫指数明显低于正常人。它反映了植物神经功能受到损伤,同时还显示心电图数据不必大量采集便能说明问题。
Analysis of Lyapunov Exponents of Heart Rate Variability in Diabetics
Zhou Liangfei Qin Mingxin
, 百拇医药
(Department of Biomedical Electronic Engineering, Fourth Military Medical University, Xi'an 710032)
Abstract This paper presents an analysis of Lyapunov exponents of ten normal persons and ten patients with diabetes mellitus by the definition of the Lyapunov exponents, the length evolution and the area evolution. The results show that the Lyapunov exponent of diabetic is clearly lower than that of normal. It can indicate the diabetic with less number of electrocardiographic data.
, http://www.100md.com
Key words Heart rate variability Lyapunov exponents Diabetes mellitus
1 引言
混沌是一种非线性现象,是一种貌似随机实为有序的现象,它除具有非线性、非周期性、非随机性外,还具有界性、确定性、自相似性以及对初始条件的敏感性等特征。现在的研究表明心率信号具有混沌特征,携带了大量神经系统的功能信息,对很多疾病具有诊断或预测价值。临床应用时是一种无创分析技术,具有重要的实用价值。采用非线性动力学方法分析心率变异是目前新的方法。混沌分析包含分维数、李雅普洛夫指数、相对分散度、柯尔莫哥洛夫熵值计算等等。本文仅就李雅普洛夫指数计算介绍几种方法,并用这几种方法分别计算10例正常人和10例糖尿病人的李雅普洛夫指数。
2 原理及计算方法
2.1 经典方法
, http://www.100md.com
如果混沌运动为f(x),则李雅普洛夫指数定义如下:
其中:f(xk)为数字时间序列;N为数据点数。
上式也给出了离散数据点的李雅普洛夫指数的计算方法。李雅普洛夫指数方法用于辅助状态空间图分析。混沌系统表现为对初始条件的敏感,在状态空间,敏感依赖表现在图上为临近轨线从最初靠近位置大大的发散。李雅普洛夫指数是这个分离速度的定量测量。指数的数量大小反映了系统的混沌程度,指数值愈大,则系统愈混沌[1]。
2.2 长度演化法
人们通常只能观测一个n维系统的某一个变量,最常见的是时间变量。对于给定的时间序列f(t),可以采用延时坐标相空间法从实验数据重构吸引子。而且重构吸引子的李氏指数谱与原吸引子的指数谱相同。我们仿照Grassberger和Procaccia根据嵌入理论和重建相空间思想从时间序列直接计算关联维数的方法来计算李氏指数。给定的时间序列f(t),m维相空间重构,给出重构吸引子上时刻t0的一个原始点,比如选取第一点。
, 百拇医药
X1=(x1,x1+τ,…,x1+(m-1)τ)
用穷举法找出该点在欧氏距离下的最近邻点。在下一个时刻t1,原始长度将演化为L’(t1)。长度元素是通过吸引子传播的,因此只能考虑足够短的时间,使得考察的是吸引子的局域结构。因为演化时间太长,L将收缩到确定它的两个轨道,它通过了吸引子的折叠区,这将导致的低估计。现在寻找新的点,它满足两个条件,L(t1)与演化置信点间隔很小,而且演化与代换元之间的角度也很小,如果找不到适当的代换点,则可保留曾使用的点,重复这一过程到置信轨道历经整个数据文件。在该点的估计值[2,3]。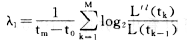
其中:M为代换步数。此方法称之为λ长度演化法,也可用下述图形来表达(图1)。
, http://www.100md.com
图1 李雅普洛夫指数长度演化法示意框图
Fig 1 A schematic representation of the evolution and replacement procedure used to estimate Lyapunov exponents from the growth of length elements
如图1所示,那么李雅普洛夫指数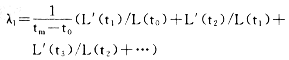
2.3 面积演化法
面积演化法考虑的是几近于平面局域结构的谱的吸引子,它可以克服长度演化法中当一条线段增大到显著大时,无法找到相同取向的较短线段的位移,则失去吸引子中最膨胀方向的意义,不能正确计算李氏指数的缺陷。下面予以介绍。
, 百拇医药
在重构吸引子中确定3个近邻点P(0),Q(0)及R(0),其中P(0)是吸引子中的任一点,比如可取第一点X1=(x1+x1+τ,…,x1+(m-1τ),对应时间t0,点Q(0)及R(0)则是用穷举法或其它方法找到P(0)的最邻近点,然后按时间序列向前发展,而求得这三个点在时刻t1的新位置记为P(1),Q(1),R(1)。这两个三角形面积记为A(t0)和A(t1)。将P(1)采用P(0)的做法求得三角形面积为A(t1)和A(t2),依次类推,李氏指数估计值为: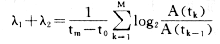
其中:tk为第k步代换的时间;M为代换总步数。也可用下述图2来表示。
, 百拇医药
图2 李雅普洛夫指数面积演化法示意框图
Fig 2 A schematic representation of the evolution and replacement procedure used to estimate Lyapunov exponents from the growth of area elements
3 检查对象和方法
3.1 检查对象
3.1.1 正常组 10例无病史且为健康年轻人,平均年龄22岁。采用自制系统,采用标准Ⅱ导联心电信号,以250 Hz的采样频率连续采样20 min。
3.1.2 糖尿病组 糖尿病植物神经病变10例,平均年龄41岁。采用自制系统,采用标准Ⅱ导联心电信号,以250 Hz的采样频率连续采样20 min。
, 百拇医药
3.2 分析方法
上述数据采用三种方法分别计算李氏指数,使用成组资料t检验,实验数据均以平均值±标准差表示,分析采用Microsoft Excel统计分析软件。
4 结果及讨论
以下是我们采用上述方法计算10例正常人和10例糖尿病人李氏指数的结果。
表1 正常人和糖尿病人李氏指数的平均结果
Table 1 Mean values of Lyapunov exponent of normals and diabetics
Definition
Length 2
, http://www.100md.com
Area 2
Length 3
Area 3
Normal
4.1±0.3
3.32±0.02
4.16±0.03
1.86±0.001
2.33±0.01
Diabetic
3.3±0.5
1.3±0.3
, http://www.100md.com
1.7±0.4
1.31±0.01
1.5±0.2
P
>0.05
<0.01
<0.01
<0.01
<0.01
其定义法指的是依据李氏指数定义来计算,长度法2维、3维代表长度法2维、3维空间重构,面积法2维、3维代表面积法2维、3维空间重构,计算程序采用Turbo C 2.0编写。
从上述结果可以明显看出,糖尿病人的李氏指数明显低于正常人,而且实验数据显示个体没有例外。它反映了植物神经功能受到损伤,因此李氏指数能反映出心率变异性,反映植物神经功能的变化。
, 百拇医药
以下是一例正常人和一例糖尿病人采用上述三种方法在不同数据量时的结果。
表2 不同数据量时正常人李氏指数的结果
Table 2 Results of Lyapunov exponent of a normal person with different numbers of R-R intervals Number
Definition
Length 2
Area 2
Length 3
Area 3
800
, 百拇医药
3.616
3.252
3.582
1.648
2.112
1000
3.701
3.284
3.686
1.680
2.139
1200
3.738
, 百拇医药
3.427
3.809
1.754
2.181
1400
3.771
3.517
3.942
1.811
2.237
1500
3.775
3.562
, 百拇医药
3.985
1.849
2.259
表3 不同数据量时糖尿病人李氏指数的结果
Table 3 Results of Lyapunov exponent of a diabetic with different numbers of R-R intervals Number
Definition
Length 2
Area 2
Length 3
Area 3
, http://www.100md.com
800
3.359
1.419
1.667
1.239
1.578
1000
3.373
1.687
1.575
1.349
1.571
1200
, http://www.100md.com
3.351
1.415
1.563
1.329
1.588
1400
3.346
1.465
1.548
1.348
1.560
1500
3.308
, http://www.100md.com
1.330
1.525
1.285
1.573
由上可以看出,数据在1000以上数值计算结果已无明显变化,我们认为不必象理论上那样采集104~106之间那么大的数据量就能估计出李氏指数,采集1500个R-R间期数据约需20 min左右的时间,这样在临床应用中是切实可行的。
从上可以看出,长度法和面积法计算李氏指数比定义法更具有显著性差异。同时还可以看出,短时心率变异分析在临床应用中具有实际意义。
参考文献
[1] 徐晓红.计算机化心动周期信号混沌分析系统.重庆医科大学硕士论文,1995;72
[2] 李后强.汪富泉著.分形理论及在分子科学中的应用.北京:科学出版社,1993∶201-206
[3] Alan W, Jack BS, Harry LS et al. Determining Lyapunov Exponents from a time series. Physical16D, 1985∶285-317
(收稿:1997-11-05 修回:1998-06-05), 百拇医药
单位:周亮飞 秦明新 (第四军医大学 生物医学工程系,西安 710032)
关键词:心率变异性;李雅普洛夫指数;糖尿病
生物医学工程学杂志990114 内容摘要 采用常规的李雅普洛夫指数定义的方法和长度演化法、面积演化法分别计算10例正常人和10例糖尿病人的李雅普洛夫指数,结果显示糖尿病人的李雅普洛夫指数明显低于正常人。它反映了植物神经功能受到损伤,同时还显示心电图数据不必大量采集便能说明问题。
Analysis of Lyapunov Exponents of Heart Rate Variability in Diabetics
Zhou Liangfei Qin Mingxin
, 百拇医药
(Department of Biomedical Electronic Engineering, Fourth Military Medical University, Xi'an 710032)
Abstract This paper presents an analysis of Lyapunov exponents of ten normal persons and ten patients with diabetes mellitus by the definition of the Lyapunov exponents, the length evolution and the area evolution. The results show that the Lyapunov exponent of diabetic is clearly lower than that of normal. It can indicate the diabetic with less number of electrocardiographic data.
, http://www.100md.com
Key words Heart rate variability Lyapunov exponents Diabetes mellitus
1 引言
混沌是一种非线性现象,是一种貌似随机实为有序的现象,它除具有非线性、非周期性、非随机性外,还具有界性、确定性、自相似性以及对初始条件的敏感性等特征。现在的研究表明心率信号具有混沌特征,携带了大量神经系统的功能信息,对很多疾病具有诊断或预测价值。临床应用时是一种无创分析技术,具有重要的实用价值。采用非线性动力学方法分析心率变异是目前新的方法。混沌分析包含分维数、李雅普洛夫指数、相对分散度、柯尔莫哥洛夫熵值计算等等。本文仅就李雅普洛夫指数计算介绍几种方法,并用这几种方法分别计算10例正常人和10例糖尿病人的李雅普洛夫指数。
2 原理及计算方法
2.1 经典方法
, http://www.100md.com
如果混沌运动为f(x),则李雅普洛夫指数定义如下:

其中:f(xk)为数字时间序列;N为数据点数。
上式也给出了离散数据点的李雅普洛夫指数的计算方法。李雅普洛夫指数方法用于辅助状态空间图分析。混沌系统表现为对初始条件的敏感,在状态空间,敏感依赖表现在图上为临近轨线从最初靠近位置大大的发散。李雅普洛夫指数是这个分离速度的定量测量。指数的数量大小反映了系统的混沌程度,指数值愈大,则系统愈混沌[1]。
2.2 长度演化法
人们通常只能观测一个n维系统的某一个变量,最常见的是时间变量。对于给定的时间序列f(t),可以采用延时坐标相空间法从实验数据重构吸引子。而且重构吸引子的李氏指数谱与原吸引子的指数谱相同。我们仿照Grassberger和Procaccia根据嵌入理论和重建相空间思想从时间序列直接计算关联维数的方法来计算李氏指数。给定的时间序列f(t),m维相空间重构,给出重构吸引子上时刻t0的一个原始点,比如选取第一点。
, 百拇医药
X1=(x1,x1+τ,…,x1+(m-1)τ)
用穷举法找出该点在欧氏距离下的最近邻点。在下一个时刻t1,原始长度将演化为L’(t1)。长度元素是通过吸引子传播的,因此只能考虑足够短的时间,使得考察的是吸引子的局域结构。因为演化时间太长,L将收缩到确定它的两个轨道,它通过了吸引子的折叠区,这将导致的低估计。现在寻找新的点,它满足两个条件,L(t1)与演化置信点间隔很小,而且演化与代换元之间的角度也很小,如果找不到适当的代换点,则可保留曾使用的点,重复这一过程到置信轨道历经整个数据文件。在该点的估计值[2,3]。
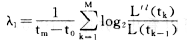
其中:M为代换步数。此方法称之为λ长度演化法,也可用下述图形来表达(图1)。

, http://www.100md.com
图1 李雅普洛夫指数长度演化法示意框图
Fig 1 A schematic representation of the evolution and replacement procedure used to estimate Lyapunov exponents from the growth of length elements
如图1所示,那么李雅普洛夫指数
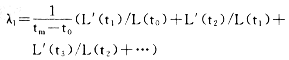
2.3 面积演化法
面积演化法考虑的是几近于平面局域结构的谱的吸引子,它可以克服长度演化法中当一条线段增大到显著大时,无法找到相同取向的较短线段的位移,则失去吸引子中最膨胀方向的意义,不能正确计算李氏指数的缺陷。下面予以介绍。
, 百拇医药
在重构吸引子中确定3个近邻点P(0),Q(0)及R(0),其中P(0)是吸引子中的任一点,比如可取第一点X1=(x1+x1+τ,…,x1+(m-1τ),对应时间t0,点Q(0)及R(0)则是用穷举法或其它方法找到P(0)的最邻近点,然后按时间序列向前发展,而求得这三个点在时刻t1的新位置记为P(1),Q(1),R(1)。这两个三角形面积记为A(t0)和A(t1)。将P(1)采用P(0)的做法求得三角形面积为A(t1)和A(t2),依次类推,李氏指数估计值为:
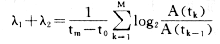
其中:tk为第k步代换的时间;M为代换总步数。也可用下述图2来表示。

, 百拇医药
图2 李雅普洛夫指数面积演化法示意框图
Fig 2 A schematic representation of the evolution and replacement procedure used to estimate Lyapunov exponents from the growth of area elements
3 检查对象和方法
3.1 检查对象
3.1.1 正常组 10例无病史且为健康年轻人,平均年龄22岁。采用自制系统,采用标准Ⅱ导联心电信号,以250 Hz的采样频率连续采样20 min。
3.1.2 糖尿病组 糖尿病植物神经病变10例,平均年龄41岁。采用自制系统,采用标准Ⅱ导联心电信号,以250 Hz的采样频率连续采样20 min。
, 百拇医药
3.2 分析方法
上述数据采用三种方法分别计算李氏指数,使用成组资料t检验,实验数据均以平均值±标准差表示,分析采用Microsoft Excel统计分析软件。
4 结果及讨论
以下是我们采用上述方法计算10例正常人和10例糖尿病人李氏指数的结果。
表1 正常人和糖尿病人李氏指数的平均结果
Table 1 Mean values of Lyapunov exponent of normals and diabetics
Definition
Length 2
, http://www.100md.com
Area 2
Length 3
Area 3
Normal
4.1±0.3
3.32±0.02
4.16±0.03
1.86±0.001
2.33±0.01
Diabetic
3.3±0.5
1.3±0.3
, http://www.100md.com
1.7±0.4
1.31±0.01
1.5±0.2
P
>0.05
<0.01
<0.01
<0.01
<0.01
其定义法指的是依据李氏指数定义来计算,长度法2维、3维代表长度法2维、3维空间重构,面积法2维、3维代表面积法2维、3维空间重构,计算程序采用Turbo C 2.0编写。
从上述结果可以明显看出,糖尿病人的李氏指数明显低于正常人,而且实验数据显示个体没有例外。它反映了植物神经功能受到损伤,因此李氏指数能反映出心率变异性,反映植物神经功能的变化。
, 百拇医药
以下是一例正常人和一例糖尿病人采用上述三种方法在不同数据量时的结果。
表2 不同数据量时正常人李氏指数的结果
Table 2 Results of Lyapunov exponent of a normal person with different numbers of R-R intervals Number
Definition
Length 2
Area 2
Length 3
Area 3
800
, 百拇医药
3.616
3.252
3.582
1.648
2.112
1000
3.701
3.284
3.686
1.680
2.139
1200
3.738
, 百拇医药
3.427
3.809
1.754
2.181
1400
3.771
3.517
3.942
1.811
2.237
1500
3.775
3.562
, 百拇医药
3.985
1.849
2.259
表3 不同数据量时糖尿病人李氏指数的结果
Table 3 Results of Lyapunov exponent of a diabetic with different numbers of R-R intervals Number
Definition
Length 2
Area 2
Length 3
Area 3
, http://www.100md.com
800
3.359
1.419
1.667
1.239
1.578
1000
3.373
1.687
1.575
1.349
1.571
1200
, http://www.100md.com
3.351
1.415
1.563
1.329
1.588
1400
3.346
1.465
1.548
1.348
1.560
1500
3.308
, http://www.100md.com
1.330
1.525
1.285
1.573
由上可以看出,数据在1000以上数值计算结果已无明显变化,我们认为不必象理论上那样采集104~106之间那么大的数据量就能估计出李氏指数,采集1500个R-R间期数据约需20 min左右的时间,这样在临床应用中是切实可行的。
从上可以看出,长度法和面积法计算李氏指数比定义法更具有显著性差异。同时还可以看出,短时心率变异分析在临床应用中具有实际意义。
参考文献
[1] 徐晓红.计算机化心动周期信号混沌分析系统.重庆医科大学硕士论文,1995;72
[2] 李后强.汪富泉著.分形理论及在分子科学中的应用.北京:科学出版社,1993∶201-206
[3] Alan W, Jack BS, Harry LS et al. Determining Lyapunov Exponents from a time series. Physical16D, 1985∶285-317
(收稿:1997-11-05 修回:1998-06-05), 百拇医药