脑电信号数据压缩及棘波识别的小波神经网络方法
作者：张永胜 刘爱萍 郁 可
单位：(张永胜)武汉工业大学 计算机科学系，武汉 430070；(刘爱萍)洛阳工业高专 计算机系，洛阳 471003；(郁可)武汉工业大学 光纤中心，武汉 430070
关键词：脑电图；小波神经网络；数据压缩；信号处理；癫痫
生物医学工程学杂志990212 摘要 在对小波神经网络及其算法研究的基础上，提出了一种对脑电信号压缩表达和痫样脑电棘波识别的新方法。实验结果显示，小波网络在大量压缩数据的同时，能够较好的恢复原有信号。另外，在脑电信号的时频谱等高线图上，得到了易于自动识别的棘波和棘慢复合波特征，说明此方法在电生理信号处理和时频分析方面有着光明的应用前景。
A Wavelet Neural Network Algorithm of EEG Signals Data
, 百拇医药
Compression and Spikes Recognition
Zhang Yongsheng Liu Aiping Yu Ke
Department of Computer Science, Wuhan University of Technology, Wuhan 430070
Departemnt of Computer, Luoyang Technology College, Luoyang 471003
Optical Fiber Sensing Research Center, Wuhan University of Technology, Wuhan 430070
Abstract A novel method of EEG signals compression representation and epileptiform spikes recognition based on wavelet neural network and its algorithm is presented. The wavelet network not only can compress data effectively but also can recover original signal. In addition, the characters of the spikes and the spike-slow rhythm are auto-detected from the time-frequency isoline of EEG signal. This method is well worth using in the field of the electrophysiological signal processing and time-frequency analyzing.
, http://www.100md.com
Key words Electroncephalograph Wavelet neural network Data compression Signal processing Epilepsy
由脑电图机记录下来的脑电信号，是进行神经系统疾病和症状特别是癫痫病诊断的主要依据。准确判定疾病的不同发作类型，选择合适的药物及治疗方案，通常需要处理庞大的脑电信号数据。在保证脑电信号主要特征基本不变的前提下对其进行压缩，较大的减少其数据量，改善其存储、检索及分类等问题，是一项很有意义的研究工作。另外，EEG中的棘波通常意味着脑功能的某种异常，棘波的极性和幅值提供了异常部位和程度的信息。临床上EEG棘波检测常用于癫痫病人的病情预报和长时间脑电监护。目前多道EEG数据必须由医生人工解释，工作量巨大。所以采用高分辨率的时频分析方法，进行痫样脑电棘波的实时自动识别，也是人们所面临的重要课题。小波神经网络，简称小波网络[1，2]是基于小波分析[3，4]所构造的一种新的神经网络，由于小波变换在处理信号时具有较好的高频域时间精度和低频域频率精度的优点，故它在压缩数据、模式识别、信噪分离等方面有着广泛应用。以小波函数构造的神经网络应用于脑电信号的压缩表达上，并在此基础上计算EEG的Wigner时频能量分布。结果表明，通过调节小波基参数、权值，网络在大量压缩数据的同时能够很好的恢复原有脑电信号，并较准确地反映各种波形的位置和强度，从而达到压缩信号与原始信号的最佳匹配。另外，通过对脑电信号时变谱结构在二维时频(地形)图上的显示，可以在一定频带上检测出痫样脑电棘波发生的位置和类型，有益于特征波的识别。
, http://www.100md.com
1 基本原理
1.1 数据压缩表达网络
小波变换实质是一种不同参数空间之间通过小波基进行的积分变换[4]。小波基是此变换的内核，选择的不同对变换起着关键的作用。小波网络则是基于小波分析而构造的新的神经网络模型，其思想是用非线性小波基取代了通常的非性Sigmoid函数，其信号表述是通过将所选取的小波基进行线性叠加来实现的，信号s(t)可用小波基进行如下拟合：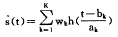
(1)
式中：(t)为拟合信号；wk、bk和aK分别为权值、小波基的平移因子和伸缩因子，k为小波基的个数。
网络参数wk、bk和ak可以通过下述最小均方误差能量函数进行优化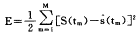
(2)
, 百拇医药
其中：M为数据采样点总数。在(1)式中采用下述Morlet母小波，该小波是余弦调制的高斯波，时频域同时分辨率高：
h(t)=cos(1.75t)exp(-t2/2) (3)
若令t′=(t-bk)/ak，则E对wk的梯度为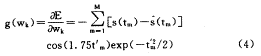
同理可计算g(bk)、g(ak)。
采用共轭梯度法优化网络wk、bk、ak分别令向量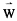
＝(W1,W2，…，Wk,…,WK)，g(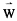)＝(g(W1)，g(W2,)…，g(Wk)，…，g(Wk)),
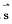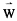()i为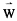第i次循环搜索方向，则
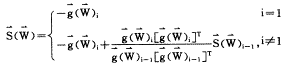(5)
, http://www.100md.com
其中：T代表转置，同理定义(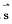
)i，(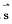
)；
W按下式进行调节，同理可按类似公式调节，
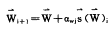(6)
我们采用了一维搜索变步长法[5]，计算最佳步长αwi，αbi，αai每次循环时，按上面式子分别调节网络参数向量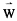、和直到E小于某一设定误差或循环结束为止。
, 百拇医药
1.2 时频能量分布计算
一旦S^(t)对s(t)的逼近达到所期望的精度，即可计算s(t)的时频能量分布，因s(t)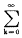
=wkh(ak,bk,t)，并且‖s(t)‖22=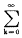｜wk｜2，故s(t)的Wigner分布为
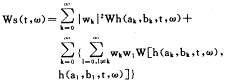(7)
式(7)中，Ws(t,ω)为s(t)的Wigner分布；Wh(ak,bk,t，ω)为小波基h(ak,bk,t)的Wigner分布；最后一项为交叉项，因为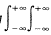
Wh(ak,bk,t,ω)dtdω=1在不损s(t)的总能量的情况下可去掉(7)式中的交叉项，从而得到没有交叉项的一种新的时频能量分布函数：
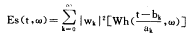(8)
, 百拇医药
其估计值为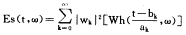
(9)
用上述方法得到的时频能量分布，经实验表明，时频域分辨率高于短时傅里叶变换(STFT)，与离散Wigner分布(DWD)相当 ，但没有因交叉干扰，而在某些区域产生的伪峰。故在真实准确反映离散信号在各个时刻所包含的频率成分方面，此方法优于STFT和DWD。
2 结果与讨论
2.1 脑电信号压缩
根据前述方法，我们对某一时段(T＝4s)的痫样脑电特征波(数字化采样频率200 Hz，共800个数据点)进行了压缩研究。将其脑电图的全部数据作为训练集，时间作为输入，幅度作为目标输出，共采用了18个小波基进行训练，将wk,ak初始值定为随机数，为了加快网络收敛速度及避免误差局部最小，以波峰和波谷等所对应的时间作为bk的初始值，训练次数为150次。开始步长分别为αw=10-2；αa=αb=10-7，训练结束后输出误差E为0.00975，将全部采样时间点作为输入对谱图进行了恢复，输出误差E也为0.00975。图1分别给出了该时段的原始和恢复后的脑电波图。
, 百拇医药
可以看出恢复后的脑电图谱能很好地保持原有图谱的特征。特别是能够较准确地反映波峰的位置和幅度。这样脑电信号原始波形的幅度数据，可以用18组wk,bk和ak共54个参数表示出来，从而实现了其信号的压缩，压缩比约为15∶1，效果是理想的。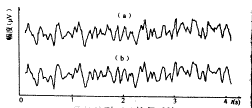
(a)原始波形；(b)恢复后波形
(a) original wvae form；(b)recovery wave form
图1 脑电图波形比较
Fig 1 Comparison of EEG wave forms
需要指出的是，小波基的多少和网络参数的初始值，对网络训练及谱图恢复程序有很大的影响。如果模拟较大时段的波谱，则随着小基个数的增加，计算量会迅速增大，于是对这计算机综合性能的要求也要提高，这就要借助于算法的进一步改进及高性计算机的应用。此外，采用不同的母小波和误差能量函数，有可能减小训练误差，加快网络收敛速度，进一步提高恢复效果，更适应实时数据压缩的要求。这些方面的问题我们也正在探索中。
, http://www.100md.com
2.2 脑电棘波，棘慢的识别
根据济南市中心医院神经内科和脑电图室记录的50例临床癫痫患者脑电图数据进行棘波的识别，这些患者都经专家确诊患有各种类型的癫痫。其中发作类型有：典型失神发作10例；全身强直阵挛发作15例；简单部分发作6例；复杂部分发作2例；儿童良性颞-中央区放电灶癫痫5例；诱发(深呼吸，闪光刺激或美解眠药物诱发)发作5例；难以分类2例；未发作有散在棘波出现5例。采样频率200 Hz。为了在较短时间内突出反映信号随时间变化的局部化特征，并加快计算速度，我们每次取时段为T＝6 s,电极分布为：1)Fp1-A1;2)Fp2-A2;3)C3-A1;4)C4-A2;5)T3-A1;6)T4-A2;7)O1-A1;8)O2-A2。
由(9)式(h(t)取Morlt小波)计算得到时频平面脑电信号的能量分布E^′Eeg(t,ω)，该能量分布在25～40 Hz的带限内进行，对最大值的归一化得E^′Eeg(t,ω)，然后对带限内的E^′Eeg(t,ω)进行过阈值判决，经多次试验阈值选定为0.8，超过阈值时说明此时有棘波发生。图2、图3、图4用等高线图的方式表示了一段EEG信号在时频平面的能量分布。
, http://www.100md.com
棘波的识别：图2为一癫痫发作期间的散在棘波时频谱图，它清晰刻画了各频率分量随时间变化的情形，给出了准确的时频定位，如显示了两个高频能量峰(即棘波发生点)A、B的发生时间。利用20～40 Hz频带上的过阈值检测同样也确定了棘波发生的A、B时刻，说明此方法具有很好的局部化特性和很高的棘波识别能力。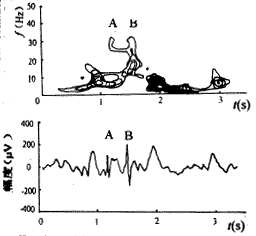
图2 有散在尖锐峰(棘波)发生的一段癫痫状脑电图
Fig 2 An epileptiform EEG containing the scattered spike
棘慢波识别：图3是一段经美解眠诱发而癫痫发作的脑电图(4道)，时频等高线图显示，在棘慢复合波出现时，在20～40 Hz左右在明显的能量分布，在3 Hz左右出现高的能量分布，利用能量过阈值检测可准确确定棘波出现的时刻，过阈值检测时，2～3 Hz可能检测到慢波或高幅运动伪差。再根据棘波与慢波间的时间关系(延迟<100 ms)可确定慢复合波的发生。
, 百拇医药
棘慢节律的识别：图4示出了一段癫痫自然发作时的脑电图及时频分布图。在20～40 Hz时有高的能量峰并且出现节律结构，这是3 次/s的节律带来的。4 Hz左右有集中的能量分布，利用棘慢波识别的步骤可确定每个棘慢波发生的时刻，连续多个棘慢波识别到时，就说明发生了棘慢节律波。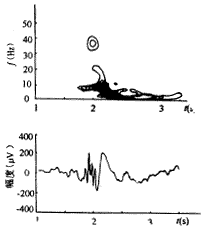
图3 具有尖锐一平缓峰(棘-慢波)复合波形的癫痫状脑电图
Fig 3 An epileptiform EEG with spike-slow complex patterm
图4 具有尖锐一平缓峰(棘-慢峰)节律的一段癫痫小发作时的脑电图
Fig 4 An epilepsy slight attack EEG with spike-slow rhythm
, 百拇医药
表1列出了痫样脑电波识别的统计结果。可见此方法自动识别与专家目测比较，对棘波和棘慢复合波的检测准确率已达到目测的水平。
3 结 论
通过对小波神经网络及其算法在脑电信号
表1 50例痫样脑电波识别的统计结果
Table 1 The statistical result of identification from 50 cases of epileptiform EEG 类别
统计项目
数量
类别
统计项目
, 百拇医药
数量
痫样脑电图中
有散在棘波发生
棘波数(目测)/个
78
痫样脑电图中
有棘慢复合波发生
棘慢波数(目测)/个
368
检出数(自动)/个
76
检出数(自动)/个
, 百拇医药
359
误检数/个
3
误检数/个
12
误检率/%
3.9%
误检率/%
3.3%
漏检数/个
2
漏检数/个
9
, http://www.100md.com
漏检率/%
2.6%
漏检率/%
2.5%
处理方面的应用研究，实现了对脑电波数据的压缩表征和棘波的自动识别，取得了令人满意的效果。实验表明，本方法具有很好的信号特征提取和屏蔽随机噪声能力，特别适用于非平稳、非线性等各种复杂结构信号的分析，有效地提供了有助于临床诊断的较多信息，并在实时信号数据压缩表征和脑电监护等方面有着好的应用前景和优越性。本方法也可用于其它电生理信号的压缩表征。
参考文献
1 Zhang Q,Benvenise A.Wavelet network. Proc IEEE Trans on Neural Network,1992;3(6)∶889
, http://www.100md.com
2 Harold HS, Brain T. Shubha K Neural network adaptive wavelet for signal representation and classification, Optical Engineering, 1992;31(9)∶1907
3 Bos M, Hoogendam E. Wavelet transform for the evaluation of peak intensities in flow injection analysis. Analytica Chemica Acta, 1992;267∶73
4 秦前清，杨宗凯.实用小波分析.西安：西安电子科技大学出版社，1995∶1-16
5 胡守仁，沈 清，胡德文等.神经网络应用技术.长沙：国防科技大学出版社，1993∶42-69
6 Alison AD.A multistage of system to detect epileptiform activity in the EEG, IEEE Trans on BME,1993;40(12)∶513
收稿：1997-11-25 修回：1998-05-07, http://www.100md.com
单位：(张永胜)武汉工业大学 计算机科学系，武汉 430070；(刘爱萍)洛阳工业高专 计算机系，洛阳 471003；(郁可)武汉工业大学 光纤中心，武汉 430070
关键词：脑电图；小波神经网络；数据压缩；信号处理；癫痫
生物医学工程学杂志990212 摘要 在对小波神经网络及其算法研究的基础上，提出了一种对脑电信号压缩表达和痫样脑电棘波识别的新方法。实验结果显示，小波网络在大量压缩数据的同时，能够较好的恢复原有信号。另外，在脑电信号的时频谱等高线图上，得到了易于自动识别的棘波和棘慢复合波特征，说明此方法在电生理信号处理和时频分析方面有着光明的应用前景。
A Wavelet Neural Network Algorithm of EEG Signals Data
, 百拇医药
Compression and Spikes Recognition
Zhang Yongsheng Liu Aiping Yu Ke
Department of Computer Science, Wuhan University of Technology, Wuhan 430070
Departemnt of Computer, Luoyang Technology College, Luoyang 471003
Optical Fiber Sensing Research Center, Wuhan University of Technology, Wuhan 430070
Abstract A novel method of EEG signals compression representation and epileptiform spikes recognition based on wavelet neural network and its algorithm is presented. The wavelet network not only can compress data effectively but also can recover original signal. In addition, the characters of the spikes and the spike-slow rhythm are auto-detected from the time-frequency isoline of EEG signal. This method is well worth using in the field of the electrophysiological signal processing and time-frequency analyzing.
, http://www.100md.com
Key words Electroncephalograph Wavelet neural network Data compression Signal processing Epilepsy
由脑电图机记录下来的脑电信号，是进行神经系统疾病和症状特别是癫痫病诊断的主要依据。准确判定疾病的不同发作类型，选择合适的药物及治疗方案，通常需要处理庞大的脑电信号数据。在保证脑电信号主要特征基本不变的前提下对其进行压缩，较大的减少其数据量，改善其存储、检索及分类等问题，是一项很有意义的研究工作。另外，EEG中的棘波通常意味着脑功能的某种异常，棘波的极性和幅值提供了异常部位和程度的信息。临床上EEG棘波检测常用于癫痫病人的病情预报和长时间脑电监护。目前多道EEG数据必须由医生人工解释，工作量巨大。所以采用高分辨率的时频分析方法，进行痫样脑电棘波的实时自动识别，也是人们所面临的重要课题。小波神经网络，简称小波网络[1，2]是基于小波分析[3，4]所构造的一种新的神经网络，由于小波变换在处理信号时具有较好的高频域时间精度和低频域频率精度的优点，故它在压缩数据、模式识别、信噪分离等方面有着广泛应用。以小波函数构造的神经网络应用于脑电信号的压缩表达上，并在此基础上计算EEG的Wigner时频能量分布。结果表明，通过调节小波基参数、权值，网络在大量压缩数据的同时能够很好的恢复原有脑电信号，并较准确地反映各种波形的位置和强度，从而达到压缩信号与原始信号的最佳匹配。另外，通过对脑电信号时变谱结构在二维时频(地形)图上的显示，可以在一定频带上检测出痫样脑电棘波发生的位置和类型，有益于特征波的识别。
, http://www.100md.com
1 基本原理
1.1 数据压缩表达网络
小波变换实质是一种不同参数空间之间通过小波基进行的积分变换[4]。小波基是此变换的内核，选择的不同对变换起着关键的作用。小波网络则是基于小波分析而构造的新的神经网络模型，其思想是用非线性小波基取代了通常的非性Sigmoid函数，其信号表述是通过将所选取的小波基进行线性叠加来实现的，信号s(t)可用小波基进行如下拟合：
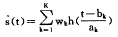(1)式中：(t)为拟合信号；wk、bk和aK分别为权值、小波基的平移因子和伸缩因子，k为小波基的个数。
网络参数wk、bk和ak可以通过下述最小均方误差能量函数进行优化
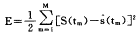(2), 百拇医药
其中：M为数据采样点总数。在(1)式中采用下述Morlet母小波，该小波是余弦调制的高斯波，时频域同时分辨率高：
h(t)=cos(1.75t)exp(-t2/2) (3)
若令t′=(t-bk)/ak，则E对wk的梯度为
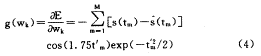
同理可计算g(bk)、g(ak)。
采用共轭梯度法优化网络wk、bk、ak分别令向量
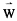＝(W1,W2，…，Wk,…,WK)，g(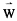)＝(g(W1)，g(W2,)…，g(Wk)，…，g(Wk)),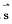(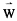)i为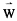第i次循环搜索方向，则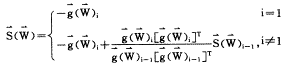(5), http://www.100md.com
其中：T代表转置，同理定义
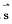()i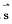，()；W按下式进行调节，同理可按类似公式调节
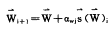， (6)我们采用了一维搜索变步长法[5]，计算最佳步长αwi，αbi，αai每次循环时，按上面式子分别调节网络参数向量
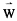、和直到E小于某一设定误差或循环结束为止。, 百拇医药
1.2 时频能量分布计算
一旦S^(t)对s(t)的逼近达到所期望的精度，即可计算s(t)的时频能量分布，因s(t)
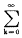=wkh(ak,bk,t)，并且‖s(t)‖22=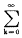｜wk｜2，故s(t)的Wigner分布为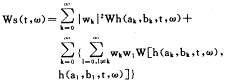(7)式(7)中，Ws(t,ω)为s(t)的Wigner分布；Wh(ak,bk,t，ω)为小波基h(ak,bk,t)的Wigner分布；最后一项为交叉项，因为
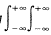Wh(ak,bk,t,ω)dtdω=1在不损s(t)的总能量的情况下可去掉(7)式中的交叉项，从而得到没有交叉项的一种新的时频能量分布函数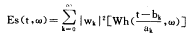： (8), 百拇医药
其估计值为
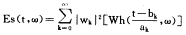(9)用上述方法得到的时频能量分布，经实验表明，时频域分辨率高于短时傅里叶变换(STFT)，与离散Wigner分布(DWD)相当 ，但没有因交叉干扰，而在某些区域产生的伪峰。故在真实准确反映离散信号在各个时刻所包含的频率成分方面，此方法优于STFT和DWD。
2 结果与讨论
2.1 脑电信号压缩
根据前述方法，我们对某一时段(T＝4s)的痫样脑电特征波(数字化采样频率200 Hz，共800个数据点)进行了压缩研究。将其脑电图的全部数据作为训练集，时间作为输入，幅度作为目标输出，共采用了18个小波基进行训练，将wk,ak初始值定为随机数，为了加快网络收敛速度及避免误差局部最小，以波峰和波谷等所对应的时间作为bk的初始值，训练次数为150次。开始步长分别为αw=10-2；αa=αb=10-7，训练结束后输出误差E为0.00975，将全部采样时间点作为输入对谱图进行了恢复，输出误差E也为0.00975。图1分别给出了该时段的原始和恢复后的脑电波图。
, 百拇医药
可以看出恢复后的脑电图谱能很好地保持原有图谱的特征。特别是能够较准确地反映波峰的位置和幅度。这样脑电信号原始波形的幅度数据，可以用18组wk,bk和ak共54个参数表示出来，从而实现了其信号的压缩，压缩比约为15∶1，效果是理想的。
(a)原始波形；(b)恢复后波形
(a) original wvae form；(b)recovery wave form
图1 脑电图波形比较
Fig 1 Comparison of EEG wave forms
需要指出的是，小波基的多少和网络参数的初始值，对网络训练及谱图恢复程序有很大的影响。如果模拟较大时段的波谱，则随着小基个数的增加，计算量会迅速增大，于是对这计算机综合性能的要求也要提高，这就要借助于算法的进一步改进及高性计算机的应用。此外，采用不同的母小波和误差能量函数，有可能减小训练误差，加快网络收敛速度，进一步提高恢复效果，更适应实时数据压缩的要求。这些方面的问题我们也正在探索中。
, http://www.100md.com
2.2 脑电棘波，棘慢的识别
根据济南市中心医院神经内科和脑电图室记录的50例临床癫痫患者脑电图数据进行棘波的识别，这些患者都经专家确诊患有各种类型的癫痫。其中发作类型有：典型失神发作10例；全身强直阵挛发作15例；简单部分发作6例；复杂部分发作2例；儿童良性颞-中央区放电灶癫痫5例；诱发(深呼吸，闪光刺激或美解眠药物诱发)发作5例；难以分类2例；未发作有散在棘波出现5例。采样频率200 Hz。为了在较短时间内突出反映信号随时间变化的局部化特征，并加快计算速度，我们每次取时段为T＝6 s,电极分布为：1)Fp1-A1;2)Fp2-A2;3)C3-A1;4)C4-A2;5)T3-A1;6)T4-A2;7)O1-A1;8)O2-A2。
由(9)式(h(t)取Morlt小波)计算得到时频平面脑电信号的能量分布E^′Eeg(t,ω)，该能量分布在25～40 Hz的带限内进行，对最大值的归一化得E^′Eeg(t,ω)，然后对带限内的E^′Eeg(t,ω)进行过阈值判决，经多次试验阈值选定为0.8，超过阈值时说明此时有棘波发生。图2、图3、图4用等高线图的方式表示了一段EEG信号在时频平面的能量分布。
, http://www.100md.com
棘波的识别：图2为一癫痫发作期间的散在棘波时频谱图，它清晰刻画了各频率分量随时间变化的情形，给出了准确的时频定位，如显示了两个高频能量峰(即棘波发生点)A、B的发生时间。利用20～40 Hz频带上的过阈值检测同样也确定了棘波发生的A、B时刻，说明此方法具有很好的局部化特性和很高的棘波识别能力。
图2 有散在尖锐峰(棘波)发生的一段癫痫状脑电图
Fig 2 An epileptiform EEG containing the scattered spike
棘慢波识别：图3是一段经美解眠诱发而癫痫发作的脑电图(4道)，时频等高线图显示，在棘慢复合波出现时，在20～40 Hz左右在明显的能量分布，在3 Hz左右出现高的能量分布，利用能量过阈值检测可准确确定棘波出现的时刻，过阈值检测时，2～3 Hz可能检测到慢波或高幅运动伪差。再根据棘波与慢波间的时间关系(延迟<100 ms)可确定慢复合波的发生。
, 百拇医药
棘慢节律的识别：图4示出了一段癫痫自然发作时的脑电图及时频分布图。在20～40 Hz时有高的能量峰并且出现节律结构，这是3 次/s的节律带来的。4 Hz左右有集中的能量分布，利用棘慢波识别的步骤可确定每个棘慢波发生的时刻，连续多个棘慢波识别到时，就说明发生了棘慢节律波。
图3 具有尖锐一平缓峰(棘-慢波)复合波形的癫痫状脑电图
Fig 3 An epileptiform EEG with spike-slow complex patterm
图4 具有尖锐一平缓峰(棘-慢峰)节律的一段癫痫小发作时的脑电图
Fig 4 An epilepsy slight attack EEG with spike-slow rhythm
, 百拇医药
表1列出了痫样脑电波识别的统计结果。可见此方法自动识别与专家目测比较，对棘波和棘慢复合波的检测准确率已达到目测的水平。
3 结 论
通过对小波神经网络及其算法在脑电信号
表1 50例痫样脑电波识别的统计结果
Table 1 The statistical result of identification from 50 cases of epileptiform EEG 类别
统计项目
数量
类别
统计项目
, 百拇医药
数量
痫样脑电图中
有散在棘波发生
棘波数(目测)/个
78
痫样脑电图中
有棘慢复合波发生
棘慢波数(目测)/个
368
检出数(自动)/个
76
检出数(自动)/个
, 百拇医药
359
误检数/个
3
误检数/个
12
误检率/%
3.9%
误检率/%
3.3%
漏检数/个
2
漏检数/个
9
, http://www.100md.com
漏检率/%
2.6%
漏检率/%
2.5%
处理方面的应用研究，实现了对脑电波数据的压缩表征和棘波的自动识别，取得了令人满意的效果。实验表明，本方法具有很好的信号特征提取和屏蔽随机噪声能力，特别适用于非平稳、非线性等各种复杂结构信号的分析，有效地提供了有助于临床诊断的较多信息，并在实时信号数据压缩表征和脑电监护等方面有着好的应用前景和优越性。本方法也可用于其它电生理信号的压缩表征。
参考文献
1 Zhang Q,Benvenise A.Wavelet network. Proc IEEE Trans on Neural Network,1992;3(6)∶889
, http://www.100md.com
2 Harold HS, Brain T. Shubha K Neural network adaptive wavelet for signal representation and classification, Optical Engineering, 1992;31(9)∶1907
3 Bos M, Hoogendam E. Wavelet transform for the evaluation of peak intensities in flow injection analysis. Analytica Chemica Acta, 1992;267∶73
4 秦前清，杨宗凯.实用小波分析.西安：西安电子科技大学出版社，1995∶1-16
5 胡守仁，沈 清，胡德文等.神经网络应用技术.长沙：国防科技大学出版社，1993∶42-69
6 Alison AD.A multistage of system to detect epileptiform activity in the EEG, IEEE Trans on BME,1993;40(12)∶513
收稿：1997-11-25 修回：1998-05-07, http://www.100md.com