分形模型的超声图像纹理分析
作者:刘 昉 程敬之
单位:西安交通大学 生物医学工程与仪器系,西安 710049
关键词:纹理分析;超声图像;分形;图像处理
生物医学工程学杂志990317 摘要 采用分形模型对超声图像进行了纹理分析,提出了肝脏超声图像具有分形的特点,结合肝脏两类不同的散射体解释了超声图像的二重分形特性,并对十例正常人、三例肝癌患者、三例肝硬化患者肝脏的临床超声图像计算了分维D,结果表明分维D是区分病变的重要特征量。根据分维D和尺度ε的综合影响,进一步提出纹理分类参数S作为区分病变的定量指标,实验结果表明参数S可以有效地区分病变。
Texture Analysis of B-Scan Image Using Fractal Dimension
Liu Fang Cheng Jingzhi
, 百拇医药
(Department of Biomedical Engineering and Instrumentation,Xi'an Jiaotong University,Xi'an 710049)
Abstract Based on the texture analysis of B-Scan image fractal model, this paper presents the liver clinical B-Scan images and their fractal characteristics. It describes the semi-fractal characteristics of B-Scan images and calculates the fractal dimension(D) of the liver B-scan images of 10 normal persons,3 patients with cancer of the liver, and 3 patients with cirrhosis of the liver. The results indicate that Fractal Dimension (D) is an important parameter in differentiating some diseases. On the basis of the influence of Fractal Dimension (D) and scale (ε),this paper suggests the texture classified parameter S. The experiment results indicate that the parameter S can be used to differentiate diseases efficiently.
, 百拇医药
Key words Texture analysis Ultrasonic image Fractals Image processing
1 引 言
超声诊断技术,因其具有无痛、无损、无离子幅射和可重复检查等优点,越来越广泛的应用于临床诊断。提高人体组织超声图像识别的可靠性、科学性,是发展这一技术应用的重要研究课题。近年来国内外不少学者做过这方面的研究,取得了一定的进展。有代表性的纹理分析方法是:一阶统计方法[1],二阶统计方法与自相关函数法[2,3],空间灰度层共现矩阵法[4],随机区域模型法[5]。但是,由于课题本身的复杂性,目前还没有有效的方法应用于临床,尚待进一步研究。
本文依据分形几何学观点,采用分形模型对超声图像进行了纹理分析,研究了分形维数与人体肝脏组织散射结构的关系,进而提出了一个分类判定指标,为临床诊断提供依据。
, http://www.100md.com
2 理 论
对生物软组织超声图像来说,可以在不同尺度上测量灰度层表面的面积,随所用尺度的改变,测量出的灰度层表面面积也随之变化,如在一定尺度范围内是分形的,则分数维为常数取值在2.0~3.0之间。本文基于Peleg[7]的双毯求表面面积确定分维的方法分析计算肝脏组织超声图像分维。
设超声图像的灰度函数为Z=g(x,y),则灰度函数是三维空间(x,y,z)中的一个表面。现在选定尺度ε,建立两个分别从上和下覆盖这个表面的毯子,上毯表示为uε(i,j),下毯表示为bε(i,j),毯子与这表面相隔ε尺度的距离,两个毯子相隔2ε尺度的距离,由上下两个毯子所包围的体积可求出该表面的面积。初始时取:
g(i,j)=uo(i,j)=bo(i,j)
, http://www.100md.com
其中:(i,j)为图像上的坐标值,对尺度ε=1,2,…,两毯的值可定义为: (1)
(1) (2)
(2)
图像点(m,n)是与(i,j)相距小于等于1的四邻域点,考虑这些点的灰度值可以确保上下毯覆盖住待测的表面。由uε和bε可以计算出双毯形成的体积: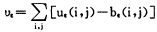
对于二维曲面,当尺度由ε-1增至ε时,所测量面积的增量为: (3)
(3)
(3)式可以测量出分形与非分形表面面积,对于纯分形的表面,其面积变化独立于尺度,而且由任意两个不同尺度所作的测量都可以提供同样的分维,因此分形表面面积还表示为(4)式(Mandelbrot[6])。
, 百拇医药
A(ε)=Fε2-D (4)
其中:F为与分形表面面积有关的幅值参数;D为分形表面的分维,用双对数坐标来画A(ε),可以获得斜率为2-D直线,由此可以在表面面积的双对数坐标图上求出分维D(fractal dimension D)及幅值参数F,对于非分形表面,将得不到直线。
3 纹理分析
为了估计分形模型对超声图像的适合程度,本文选取3例正常人肝脏超声图像,分别取肝实质图像大小60×60像素ROI(region of interest)区域,采用双毯方法计算出各自的A(ε),其中ε=1,2,…,50,并在图1中画出各自的双对数坐标图,用最小二乘法线性回归拟合出直线的斜率K,由
K=2-D
计算出分维D。
, http://www.100md.com
图1 正常肝脏超声图像的A(ε)双对数坐标图
Fig 1 B-Scan images with plots of their associated areas A(ε) on a log-log scale
由图1分析可得:
(1)超声图像的A(ε)双对数坐标图在一定尺度范围内均为分段的直线,其斜率均满足-1
(2)正常肝脏超声图像的A(ε)双对数坐标图的主要部分分为两段直线I区及Ⅱ区,所以超声图像是二重分形的(semifractal)。
(3)不同人体正常肝脏超声图像在I区及Ⅱ区具有相近的分维值,本文对10例正常肝脏的分维统计发现,误差在±0.02,这表明分维是肝脏超声图像的重要特征量。
, http://www.100md.com
超声图像具有二重分形特性,我们认为是与肝脏组织中主要存在着两种不同类型的散射结构有关,一种是弥漫散射(diffuse scatterin-
g);另一种是规则性散射(regular scattering)[2]。如肝脏组织中胶原蛋白、胆管的散射元是许多随机分布的散射元(randomly distributed scatters),大小在μm级,超声分辨体积元内含有大量此种散射子,它们的散射波相位均匀分布在0~2π内,换能器所接收的回波声压是该分辩元内所有这些散射子背向散射波的叠架结果。由于各分辨元的散射子数目及各散射波到达换能器表面的相位都是随机的,因此总的合成信号也是随机起伏的,这些散射元将产生弥漫性散射,在超声图像上表现为斑纹噪声(speckle)。另一方面,肝小叶等规则性排列的散射元是一准周期的可分辨散射元(quasi-periodic scatters),这种散射元将产生相干散射(规则散射)。对肝脏超声图像进行平滑处理,主要削弱斑纹噪声并使图像边界模糊,图2表示了同一超声图像进行m=0,1,2级平滑处理后A(ε)的双对数坐标图。从图2可以看出,平滑处理使I区的分维D1明显减小,而对Ⅱ区的D2影响很小,这表明这两种散射结构对超声图像的影响随着尺度的变化是不同的,但都是分形的。相对而言,弥漫性散射的影响在较小的尺度上表现出来,即图1的I区;规则性散射的影响在较大的尺度上表现出来,即图1的Ⅱ区。
, http://www.100md.com
图2 m=0,1,2级平滑处理的双对数坐标图
Fig 2 Smooth processing of B-scan images with plots of their associated areas A(ε) on a log-log scale
当肝脏组织出现病变时,这两种散射元将发生变化,使组织的散射回波信号改变,超声图像的分维明显偏离正常值。选取3例肝硬化(cirrhosis)、3例肝癌(cancer)患者超声图像同上方法进行计算。图3为肝硬化患者与正常肝脏超声图像的A(ε)双对数坐标图。图4为肝癌患者与正常肝脏超声图像的A(ε)双对数坐标图。表1为分维D的统计结果。
图3 (a),(b),(c)分别是3例肝硬化患者与正常人肝脏超声图像的A(ε)双对数坐标图
, 百拇医药
Fig 3 B-scan images of cirrhosis and normal with plots of their associated areas A(ε) on a log-log scale
图4 (a),(b),(c)分别是3例肝癌患者与正常人肝脏超声图像的A(ε)双对数坐标图
Fig 4 B-scan images of cancer and normal with plots of their associated areas A(ε) on a log-log scale
从图3、图4分析可得:
(1)肝硬化患者超声图像是二重分形的,与正常情况相比,Ⅰ区与Ⅱ区分界点的尺度ε变大,D1减小,D2变大。
, http://www.100md.com
(2)肝癌患者超声图像已基本变成一重分形的,与正常情况相比,D1和D2大幅度变化。
(3)相同类型的肝脏超声图像(正常的或肝硬化的或肝癌的),具有几乎相同的分形结构,这表明肝脏组织的散射结构与其超声图像的分形结构之间有密切的关系,其相关关系反映在分维D随尺度ε的变化上。
综上分析,分维的大小反映了在各自的尺度上灰度图像表面的粗糙程度,数值越大表面越粗糙,因此在理想情况下(超声图像消除引起失真的种种影响因素),分维的数值在一定意义上定量反映了散射结构的变化规律,即分维D可作为识别肝脏组织超声图像的重要指标(见表1)。
表1 肝脏超声图像的分维
Table 1 The fractal dimension of liver B-scan image Group
, http://www.100md.com
N
Fractal dimension
D1
Fractal dimension
D2
Normal
10
2.900±0.022
2.343±0.023
Cirrhosis
3
2.808~2.756
, http://www.100md.com
2.588~2.571
Cancer
3
2.688~2.694
2.696~2.698
4 纹理分类
根据上述分析,正常肝脏与发生病变肝脏的分类与分维D有关,而D在不同的尺度范围内为不同常数。因此,本文综合考虑D和ε的影响,提出纹理分类参数S用于区分病变肝脏与正常肝脏超声图像,S的表达式为: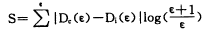 (5)
(5)
其中:Dc(ε)为10例正常人肝脏的尺度ε的分维统计平均值;Di(ε)为某一被测肝脏超声图像在尺度ε的分维值,ε=1,2,…,50。
, 百拇医药
表2为参数S的计算结果。
表2 肝脏超声图像的S值
Table 2 S parameter of liver B-scan image Parameter
Normal
(n=10)
Cirrhosis
(n=3)
Cancer
(n=3)
S
0.008~0.024
, http://www.100md.com
0.205~0.243
0.331~0.340
从表2数值可以看出对同一病症参数S的数值接近,对于不同的病症参数S具有很大的差别,因此本文将参数S作为超声图像纹理分类的指标。
5 结 论
超声图像由于受各种复杂随机因素的影响,很难用定量指标来表示,因此目前临床诊断以定性描述为主。本文通过分形模型的纹理分析,提出了肝脏超声图像具有统计自相似的分形特点,结合肝脏两类不同的散射体解释了超声图像的二重分形特性,并对10例正常肝脏、3例肝癌患者、3例肝硬化患者的临床超声图像计算了分维D,结果表明分维D是区分病变的重要特征量。根据分维D和尺度ε的综合影响,我们进一步提出了纹理分类参数S作为区分组织病变的定量指标,实验结果表明可以有效区分病变,为临床诊断展示了美好前景。
, http://www.100md.com
参考文献
1 Burckhardt CB. Speckle in ultrasound B-mode scans. IEEE Trans,1978;su-25∶1
2 Insana MF, Wagner RF, Garra BS et al. Analysis of ultrasound image texture via generalized rician statistics. Opt, Eng,1986;25(6)∶743
3 Wagner RF, Insana MF, Brown DG. Unified approach to the detection and classification of speckle texture in diagnostic. Ultrasound, Opt, Eng,1986;25(6)∶738
, 百拇医药
4 Garra BS, Krasner BH, Horii SC et al. The value of sonographic texture analysis. Ultrasonic Imaging, 1993;15∶267
5 Bleck JS, Ranft U, Gebel M et al. Random field models in the textural analysis of ultrasonic images of the liver. IEEE Trnas on medical Imaging,1996;15(6)∶796
6 Pentland AP. Fractal based description of natural scenes. IEEE Trans Pattern Analysis Mach Zntell,1984;PAMI-6(6)∶661
7 Peleg S, Naor J, Hartley R. Multiple resolution texture analysis and classification. IEEE Trans Pattern Analysis Mach Intell,1984;PAMI-6(4)∶518
(收稿:1998-03-27), http://www.100md.com
单位:西安交通大学 生物医学工程与仪器系,西安 710049
关键词:纹理分析;超声图像;分形;图像处理
生物医学工程学杂志990317 摘要 采用分形模型对超声图像进行了纹理分析,提出了肝脏超声图像具有分形的特点,结合肝脏两类不同的散射体解释了超声图像的二重分形特性,并对十例正常人、三例肝癌患者、三例肝硬化患者肝脏的临床超声图像计算了分维D,结果表明分维D是区分病变的重要特征量。根据分维D和尺度ε的综合影响,进一步提出纹理分类参数S作为区分病变的定量指标,实验结果表明参数S可以有效地区分病变。
Texture Analysis of B-Scan Image Using Fractal Dimension
Liu Fang Cheng Jingzhi
, 百拇医药
(Department of Biomedical Engineering and Instrumentation,Xi'an Jiaotong University,Xi'an 710049)
Abstract Based on the texture analysis of B-Scan image fractal model, this paper presents the liver clinical B-Scan images and their fractal characteristics. It describes the semi-fractal characteristics of B-Scan images and calculates the fractal dimension(D) of the liver B-scan images of 10 normal persons,3 patients with cancer of the liver, and 3 patients with cirrhosis of the liver. The results indicate that Fractal Dimension (D) is an important parameter in differentiating some diseases. On the basis of the influence of Fractal Dimension (D) and scale (ε),this paper suggests the texture classified parameter S. The experiment results indicate that the parameter S can be used to differentiate diseases efficiently.
, 百拇医药
Key words Texture analysis Ultrasonic image Fractals Image processing
1 引 言
超声诊断技术,因其具有无痛、无损、无离子幅射和可重复检查等优点,越来越广泛的应用于临床诊断。提高人体组织超声图像识别的可靠性、科学性,是发展这一技术应用的重要研究课题。近年来国内外不少学者做过这方面的研究,取得了一定的进展。有代表性的纹理分析方法是:一阶统计方法[1],二阶统计方法与自相关函数法[2,3],空间灰度层共现矩阵法[4],随机区域模型法[5]。但是,由于课题本身的复杂性,目前还没有有效的方法应用于临床,尚待进一步研究。
本文依据分形几何学观点,采用分形模型对超声图像进行了纹理分析,研究了分形维数与人体肝脏组织散射结构的关系,进而提出了一个分类判定指标,为临床诊断提供依据。
, http://www.100md.com
2 理 论
对生物软组织超声图像来说,可以在不同尺度上测量灰度层表面的面积,随所用尺度的改变,测量出的灰度层表面面积也随之变化,如在一定尺度范围内是分形的,则分数维为常数取值在2.0~3.0之间。本文基于Peleg[7]的双毯求表面面积确定分维的方法分析计算肝脏组织超声图像分维。
设超声图像的灰度函数为Z=g(x,y),则灰度函数是三维空间(x,y,z)中的一个表面。现在选定尺度ε,建立两个分别从上和下覆盖这个表面的毯子,上毯表示为uε(i,j),下毯表示为bε(i,j),毯子与这表面相隔ε尺度的距离,两个毯子相隔2ε尺度的距离,由上下两个毯子所包围的体积可求出该表面的面积。初始时取:
g(i,j)=uo(i,j)=bo(i,j)
, http://www.100md.com
其中:(i,j)为图像上的坐标值,对尺度ε=1,2,…,两毯的值可定义为:
 (1)
(1) (2)
(2)图像点(m,n)是与(i,j)相距小于等于1的四邻域点,考虑这些点的灰度值可以确保上下毯覆盖住待测的表面。由uε和bε可以计算出双毯形成的体积:
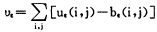
对于二维曲面,当尺度由ε-1增至ε时,所测量面积的增量为:
 (3)
(3)(3)式可以测量出分形与非分形表面面积,对于纯分形的表面,其面积变化独立于尺度,而且由任意两个不同尺度所作的测量都可以提供同样的分维,因此分形表面面积还表示为(4)式(Mandelbrot[6])。
, 百拇医药
A(ε)=Fε2-D (4)
其中:F为与分形表面面积有关的幅值参数;D为分形表面的分维,用双对数坐标来画A(ε),可以获得斜率为2-D直线,由此可以在表面面积的双对数坐标图上求出分维D(fractal dimension D)及幅值参数F,对于非分形表面,将得不到直线。
3 纹理分析
为了估计分形模型对超声图像的适合程度,本文选取3例正常人肝脏超声图像,分别取肝实质图像大小60×60像素ROI(region of interest)区域,采用双毯方法计算出各自的A(ε),其中ε=1,2,…,50,并在图1中画出各自的双对数坐标图,用最小二乘法线性回归拟合出直线的斜率K,由
K=2-D
计算出分维D。

, http://www.100md.com
图1 正常肝脏超声图像的A(ε)双对数坐标图
Fig 1 B-Scan images with plots of their associated areas A(ε) on a log-log scale
由图1分析可得:
(1)超声图像的A(ε)双对数坐标图在一定尺度范围内均为分段的直线,其斜率均满足-1
(2)正常肝脏超声图像的A(ε)双对数坐标图的主要部分分为两段直线I区及Ⅱ区,所以超声图像是二重分形的(semifractal)。
(3)不同人体正常肝脏超声图像在I区及Ⅱ区具有相近的分维值,本文对10例正常肝脏的分维统计发现,误差在±0.02,这表明分维是肝脏超声图像的重要特征量。
, http://www.100md.com
超声图像具有二重分形特性,我们认为是与肝脏组织中主要存在着两种不同类型的散射结构有关,一种是弥漫散射(diffuse scatterin-
g);另一种是规则性散射(regular scattering)[2]。如肝脏组织中胶原蛋白、胆管的散射元是许多随机分布的散射元(randomly distributed scatters),大小在μm级,超声分辨体积元内含有大量此种散射子,它们的散射波相位均匀分布在0~2π内,换能器所接收的回波声压是该分辩元内所有这些散射子背向散射波的叠架结果。由于各分辨元的散射子数目及各散射波到达换能器表面的相位都是随机的,因此总的合成信号也是随机起伏的,这些散射元将产生弥漫性散射,在超声图像上表现为斑纹噪声(speckle)。另一方面,肝小叶等规则性排列的散射元是一准周期的可分辨散射元(quasi-periodic scatters),这种散射元将产生相干散射(规则散射)。对肝脏超声图像进行平滑处理,主要削弱斑纹噪声并使图像边界模糊,图2表示了同一超声图像进行m=0,1,2级平滑处理后A(ε)的双对数坐标图。从图2可以看出,平滑处理使I区的分维D1明显减小,而对Ⅱ区的D2影响很小,这表明这两种散射结构对超声图像的影响随着尺度的变化是不同的,但都是分形的。相对而言,弥漫性散射的影响在较小的尺度上表现出来,即图1的I区;规则性散射的影响在较大的尺度上表现出来,即图1的Ⅱ区。

, http://www.100md.com
图2 m=0,1,2级平滑处理的双对数坐标图
Fig 2 Smooth processing of B-scan images with plots of their associated areas A(ε) on a log-log scale
当肝脏组织出现病变时,这两种散射元将发生变化,使组织的散射回波信号改变,超声图像的分维明显偏离正常值。选取3例肝硬化(cirrhosis)、3例肝癌(cancer)患者超声图像同上方法进行计算。图3为肝硬化患者与正常肝脏超声图像的A(ε)双对数坐标图。图4为肝癌患者与正常肝脏超声图像的A(ε)双对数坐标图。表1为分维D的统计结果。

图3 (a),(b),(c)分别是3例肝硬化患者与正常人肝脏超声图像的A(ε)双对数坐标图
, 百拇医药
Fig 3 B-scan images of cirrhosis and normal with plots of their associated areas A(ε) on a log-log scale

图4 (a),(b),(c)分别是3例肝癌患者与正常人肝脏超声图像的A(ε)双对数坐标图
Fig 4 B-scan images of cancer and normal with plots of their associated areas A(ε) on a log-log scale
从图3、图4分析可得:
(1)肝硬化患者超声图像是二重分形的,与正常情况相比,Ⅰ区与Ⅱ区分界点的尺度ε变大,D1减小,D2变大。
, http://www.100md.com
(2)肝癌患者超声图像已基本变成一重分形的,与正常情况相比,D1和D2大幅度变化。
(3)相同类型的肝脏超声图像(正常的或肝硬化的或肝癌的),具有几乎相同的分形结构,这表明肝脏组织的散射结构与其超声图像的分形结构之间有密切的关系,其相关关系反映在分维D随尺度ε的变化上。
综上分析,分维的大小反映了在各自的尺度上灰度图像表面的粗糙程度,数值越大表面越粗糙,因此在理想情况下(超声图像消除引起失真的种种影响因素),分维的数值在一定意义上定量反映了散射结构的变化规律,即分维D可作为识别肝脏组织超声图像的重要指标(见表1)。
表1 肝脏超声图像的分维
Table 1 The fractal dimension of liver B-scan image Group
, http://www.100md.com
N
Fractal dimension
D1
Fractal dimension
D2
Normal
10
2.900±0.022
2.343±0.023
Cirrhosis
3
2.808~2.756
, http://www.100md.com
2.588~2.571
Cancer
3
2.688~2.694
2.696~2.698
4 纹理分类
根据上述分析,正常肝脏与发生病变肝脏的分类与分维D有关,而D在不同的尺度范围内为不同常数。因此,本文综合考虑D和ε的影响,提出纹理分类参数S用于区分病变肝脏与正常肝脏超声图像,S的表达式为:
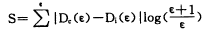 (5)
(5)其中:Dc(ε)为10例正常人肝脏的尺度ε的分维统计平均值;Di(ε)为某一被测肝脏超声图像在尺度ε的分维值,ε=1,2,…,50。
, 百拇医药
表2为参数S的计算结果。
表2 肝脏超声图像的S值
Table 2 S parameter of liver B-scan image Parameter
Normal
(n=10)
Cirrhosis
(n=3)
Cancer
(n=3)
S
0.008~0.024
, http://www.100md.com
0.205~0.243
0.331~0.340
从表2数值可以看出对同一病症参数S的数值接近,对于不同的病症参数S具有很大的差别,因此本文将参数S作为超声图像纹理分类的指标。
5 结 论
超声图像由于受各种复杂随机因素的影响,很难用定量指标来表示,因此目前临床诊断以定性描述为主。本文通过分形模型的纹理分析,提出了肝脏超声图像具有统计自相似的分形特点,结合肝脏两类不同的散射体解释了超声图像的二重分形特性,并对10例正常肝脏、3例肝癌患者、3例肝硬化患者的临床超声图像计算了分维D,结果表明分维D是区分病变的重要特征量。根据分维D和尺度ε的综合影响,我们进一步提出了纹理分类参数S作为区分组织病变的定量指标,实验结果表明可以有效区分病变,为临床诊断展示了美好前景。
, http://www.100md.com
参考文献
1 Burckhardt CB. Speckle in ultrasound B-mode scans. IEEE Trans,1978;su-25∶1
2 Insana MF, Wagner RF, Garra BS et al. Analysis of ultrasound image texture via generalized rician statistics. Opt, Eng,1986;25(6)∶743
3 Wagner RF, Insana MF, Brown DG. Unified approach to the detection and classification of speckle texture in diagnostic. Ultrasound, Opt, Eng,1986;25(6)∶738
, 百拇医药
4 Garra BS, Krasner BH, Horii SC et al. The value of sonographic texture analysis. Ultrasonic Imaging, 1993;15∶267
5 Bleck JS, Ranft U, Gebel M et al. Random field models in the textural analysis of ultrasonic images of the liver. IEEE Trnas on medical Imaging,1996;15(6)∶796
6 Pentland AP. Fractal based description of natural scenes. IEEE Trans Pattern Analysis Mach Zntell,1984;PAMI-6(6)∶661
7 Peleg S, Naor J, Hartley R. Multiple resolution texture analysis and classification. IEEE Trans Pattern Analysis Mach Intell,1984;PAMI-6(4)∶518
(收稿:1998-03-27), http://www.100md.com