高阶多层神经网络与脑电诊断
作者：刘建成 蔡湛宇
单位：(广州珠江医院 计算机室，广州 510282)
关键词：特征；高阶多层神经网络；识别
生物医学工程学杂志990418 摘要 高阶多层非线性连续时间神经网络被引入到脑电信号的识别中，实验表明其识别率可达到较理想结果。
High Order Multi-layer Neural Networks and EEG Diagnosing
Liu Jiancheng Cai Zhanyu
(Department of Computer,Zhujiang Hospital,Guangzhou 510282)
, 百拇医药
Abstract In this experiment,high-order multi-layer neural networks was introduced into the identification of EEG signal.The result of testing demonstrated that the identification rate reached an a satisfying level.
Key words Characteristic Multi-layer neural networks Identificaion
1 脑电信号特征参数的提取
研究4种不同类型的脑电信号(偏头痛，脑栓塞，癫痫，脑瘫)的特征，有关这些脑疾病与波形特征分量的关系见文献[2]，经过采样预处理，进行选择，取得病理特征提取，建立网络识别的样本集。
, 百拇医药
2 网络结构及算法
高阶神经网络比一阶有更强的鲁棒性和更强的模式分辨率，高阶多层神经网络(HMNN)[1]的一种特殊情形是循环高阶多层前馈神经网络(RHMNN)。这种网络的各层神经元数目相同，并且各层之间的连接权值矩阵相等，即：Wijk(l)=Wijk,l≤i,j,k≤N,l为层变量。它的结构和算法可参考文献[1]。有N个可能状态{qi,i=1,2…，N}及其状态之间的转移概率结构表示为：wij=Pr(qj在第一层，qi在第二层)；wijk=Pr(qk在第l+1层)；初始状态概率πi=Pr；在初始层；第i个状态产生观察值序列{vt}的概率，fi(vt)=Pr(ot=vt/qi)在第l层。而高阶隐马尔柯夫模型(HMM’s)与高阶神经网络有着内在联系。例如二阶HMM's可作为高阶神经网络的一种特殊情形。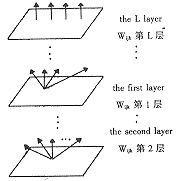
, 百拇医药
图 二阶HMM神经网络结构
Fig Structure of two order multilayer feedforward neural networks
图中所示一种二阶HMM的每层神经网络由它在时刻t和t-1的状态构成，给定任意输入(样本)模式序列O=(o1，o2…，ol)和二阶隐马尔柯夫模型λ=(πi,wij,Wijk,fk),πi为初始概率。二阶HMM的学习过程就是迭代地调整模型参数：(πi,wij,Wijk,fk),从而使计算事件概率Pr(O/λ)最大。学习过程采用Baum-Welch算法作为二阶HMM的学习过程训练算法。网络学习目的就是迭代出一组新的模型参数λ=πi,wij,Wijk,fk),使下式[2]最大。
(1)
, 百拇医药
其中ajk(l+1)=ujk(l+1+fk(ol+1),ujk(l+1)=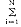
Wijk αij(l),aij(l)=πifi(o2)wijfj(o2).
Wijk(l+2)为第l层的第i个神经元和第l+1层的第j个神经元到第l+2层的第k个神经元的二阶连接权值。Ujk(l)为l层地神经元netjk(l)的输入值，ajk(l)为神经元netjk(l)的输出激励值，aij为初始值。初始连接权矩阵[3]为
(2)
, 百拇医药
其中：δij为隐层反向误差传播函数。利用梯度下降法，导出一组模型参数，权矩阵Wijk的迭代[3]为
(3)
(4)
其中：δjk为反向传播为误差函数；fk为观察值概率。
3 实验结果
建立一个高阶多层神经网络，输入节点为30个，输出节点作为最后诊断输出，隐含节点为可调整作为脑电信号特征抽取的集合，用误差允许范围内的50种脑电模拟样本进行学习。用数千个受试者的脑电图，测试过程所选50种样本与学习样本的汉明矩为2.5，先用等时间间隔采样，和传统的计算机分析方法测出它们所属的类型。从几类这随机取数，组成训练组。
, 百拇医药
表1 网络的识别率与阶数，隐节点，初始值的关系(初始值wij=0.03)
Table 1 The relationship of networks identification rate with order number,hidden nodes and initial(Initial wij=0.03)
隐节点(hidden nodes)
2
4
6
8
10
12
, 百拇医药
14
1
0.53
0.85
0.82
0.75
0.67
0.89
0.85
2
0.72
0.92
0.79
, http://www.100md.com
0.965
0.98
0.97
0.96
3
0.79
0.84
0.945
0.97
0.98
0.96
0.954
4
, 百拇医药
0.84
0.905
0.99
0.91
0.95
0.98
0.975
5
0.81
0.955
0.924
0.99
0.964
, http://www.100md.com
0.99
0.95
迭代次数
Iterations
9867
5342
5321
7810
1690
12963
12521
表2 网络的识别率与阶数，隐节点，初始值的关系(初始值wij=0.14)
, 百拇医药
Table 2 The relationship of networks identification rate with order number,hidden nodes and initial(Initial wij=0.14)
隐节点(hidden nodes)
2
4
6
8
10
12
14
1
, http://www.100md.com
0.56
0.88
0.87
0.78
0.69
0.90
0.85
2
0.70
0.90
0.81
0.925
0.95
, 百拇医药
0.90
0.98
3
0.79
0.87
0.955
0.94
0.948
0.97
0.975
4
0.89
0.90
, 百拇医药
0.99
0.90
0.955
0.955
0.975
5
0.80
0.925
0.925
0.99
0.954
0.99
0.98
, 百拇医药
迭代次数
Iterations
5673
2372
1276
1632
3290
1563
2110
由表1，2的识别率可知2阶以上的比平常1阶的网络要高，在1～5阶内阶数越高，相对的识别率水平会好些。节点数不能太小，如果太多网络权的调整时间增加，识别率没有提高，表2看出优于表1，说明初始权值的选取也将影响网络性能。表中最佳的节点为6，阶数为4的点。实际应用时，为提高网络识别率，例如初始权、节点数、学习步长等要根据运用中寻找合适的参数。 参考文献
1 Gustavsson I.A theoretical analysis of recursive identification mcthods.Automation,1978；14(3)∶231
本期数据不全, 百拇医药
单位：(广州珠江医院 计算机室，广州 510282)
关键词：特征；高阶多层神经网络；识别
生物医学工程学杂志990418 摘要 高阶多层非线性连续时间神经网络被引入到脑电信号的识别中，实验表明其识别率可达到较理想结果。
High Order Multi-layer Neural Networks and EEG Diagnosing
Liu Jiancheng Cai Zhanyu
(Department of Computer,Zhujiang Hospital,Guangzhou 510282)
, 百拇医药
Abstract In this experiment,high-order multi-layer neural networks was introduced into the identification of EEG signal.The result of testing demonstrated that the identification rate reached an a satisfying level.
Key words Characteristic Multi-layer neural networks Identificaion
1 脑电信号特征参数的提取
研究4种不同类型的脑电信号(偏头痛，脑栓塞，癫痫，脑瘫)的特征，有关这些脑疾病与波形特征分量的关系见文献[2]，经过采样预处理，进行选择，取得病理特征提取，建立网络识别的样本集。
, 百拇医药
2 网络结构及算法
高阶神经网络比一阶有更强的鲁棒性和更强的模式分辨率，高阶多层神经网络(HMNN)[1]的一种特殊情形是循环高阶多层前馈神经网络(RHMNN)。这种网络的各层神经元数目相同，并且各层之间的连接权值矩阵相等，即：Wijk(l)=Wijk,l≤i,j,k≤N,l为层变量。它的结构和算法可参考文献[1]。有N个可能状态{qi,i=1,2…，N}及其状态之间的转移概率结构表示为：wij=Pr(qj在第一层，qi在第二层)；wijk=Pr(qk在第l+1层)；初始状态概率πi=Pr；在初始层；第i个状态产生观察值序列{vt}的概率，fi(vt)=Pr(ot=vt/qi)在第l层。而高阶隐马尔柯夫模型(HMM’s)与高阶神经网络有着内在联系。例如二阶HMM's可作为高阶神经网络的一种特殊情形。
, 百拇医药
图 二阶HMM神经网络结构
Fig Structure of two order multilayer feedforward neural networks
图中所示一种二阶HMM的每层神经网络由它在时刻t和t-1的状态构成，给定任意输入(样本)模式序列O=(o1，o2…，ol)和二阶隐马尔柯夫模型λ=(πi,wij,Wijk,fk),πi为初始概率。二阶HMM的学习过程就是迭代地调整模型参数：(πi,wij,Wijk,fk),从而使计算事件概率Pr(O/λ)最大。学习过程采用Baum-Welch算法作为二阶HMM的学习过程训练算法。网络学习目的就是迭代出一组新的模型参数λ=πi,wij,Wijk,fk),使下式[2]最大。
(1), 百拇医药
其中ajk(l+1)=ujk(l+1+fk(ol+1),ujk(l+1)=
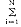Wijk αij(l),aij(l)=πifi(o2)wijfj(o2).Wijk(l+2)为第l层的第i个神经元和第l+1层的第j个神经元到第l+2层的第k个神经元的二阶连接权值。Ujk(l)为l层地神经元netjk(l)的输入值，ajk(l)为神经元netjk(l)的输出激励值，aij为初始值。初始连接权矩阵[3]为
(2), 百拇医药
其中：δij为隐层反向误差传播函数。利用梯度下降法，导出一组模型参数，权矩阵Wijk的迭代[3]为
(3) (4)其中：δjk为反向传播为误差函数；fk为观察值概率。
3 实验结果
建立一个高阶多层神经网络，输入节点为30个，输出节点作为最后诊断输出，隐含节点为可调整作为脑电信号特征抽取的集合，用误差允许范围内的50种脑电模拟样本进行学习。用数千个受试者的脑电图，测试过程所选50种样本与学习样本的汉明矩为2.5，先用等时间间隔采样，和传统的计算机分析方法测出它们所属的类型。从几类这随机取数，组成训练组。
, 百拇医药
表1 网络的识别率与阶数，隐节点，初始值的关系(初始值wij=0.03)
Table 1 The relationship of networks identification rate with order number,hidden nodes and initial(Initial wij=0.03)
隐节点(hidden nodes)
2
4
6
8
10
12
, 百拇医药
14
1
0.53
0.85
0.82
0.75
0.67
0.89
0.85
2
0.72
0.92
0.79
, http://www.100md.com
0.965
0.98
0.97
0.96
3
0.79
0.84
0.945
0.97
0.98
0.96
0.954
4
, 百拇医药
0.84
0.905
0.99
0.91
0.95
0.98
0.975
5
0.81
0.955
0.924
0.99
0.964
, http://www.100md.com
0.99
0.95
迭代次数
Iterations
9867
5342
5321
7810
1690
12963
12521
表2 网络的识别率与阶数，隐节点，初始值的关系(初始值wij=0.14)
, 百拇医药
Table 2 The relationship of networks identification rate with order number,hidden nodes and initial(Initial wij=0.14)
隐节点(hidden nodes)
2
4
6
8
10
12
14
1
, http://www.100md.com
0.56
0.88
0.87
0.78
0.69
0.90
0.85
2
0.70
0.90
0.81
0.925
0.95
, 百拇医药
0.90
0.98
3
0.79
0.87
0.955
0.94
0.948
0.97
0.975
4
0.89
0.90
, 百拇医药
0.99
0.90
0.955
0.955
0.975
5
0.80
0.925
0.925
0.99
0.954
0.99
0.98
, 百拇医药
迭代次数
Iterations
5673
2372
1276
1632
3290
1563
2110
由表1，2的识别率可知2阶以上的比平常1阶的网络要高，在1～5阶内阶数越高，相对的识别率水平会好些。节点数不能太小，如果太多网络权的调整时间增加，识别率没有提高，表2看出优于表1，说明初始权值的选取也将影响网络性能。表中最佳的节点为6，阶数为4的点。实际应用时，为提高网络识别率，例如初始权、节点数、学习步长等要根据运用中寻找合适的参数。 参考文献
1 Gustavsson I.A theoretical analysis of recursive identification mcthods.Automation,1978；14(3)∶231
本期数据不全, 百拇医药