人体小腿受冲击载荷作用时的生物动力响应
作者：王西十 白瑞蒲 S.Turgut Tumer
单位：王西十 白瑞蒲(河北大学 数学系，保定 071002)；S.Turgut Tumer(Department of Mechanical Engineering, Middle East Technical University, Ankara-6531, Turkey)
关键词：人体小腿；冲击载荷；生物动力响应
生物医学工程学杂志000210 摘要 建立了人体下肢大腿固定而小腿在矢状面内运动时的生物动力模型，并对这类数学模型的求解，发展了一种有效且易于使用的解法技术。作为应用，计算了当小腿在胫骨质量中心遭受冲击载荷时，由此而引起的膝关节咬合接触力、膝关节处的4个主要韧带所承受的张力以及膝关节股骨与胫骨咬合时的接触点的位置、小腿的前后屈伸位移和运动轨迹等。
Biodynamic Response of the Human Shank Subjected to Impulse Load
, 百拇医药
Wang Xishi Bai Ruipu
(Department of Mathematics, Hebei University, Baoding 071002)
S.Turgut Tumer
(Department of Mechanical Engineering, Middle East Technical University,Ankara-6531, Turkey)
Abstract This paper reported the establishment of biodynamic modelling of the human shank in the sagittal palne while the human thigh is fixed. And when the shank is subjected to the two types of externally applied impulse loads, the forces associated with the four main ligaments, as well as the bone-to-bone contact forces in the knee joint are numerically obtained. The contact point locations are also presented together with the angular motions of the lower limb segments.
, 百拇医药
Key words Human shank Impulse load Biodynamic response
1 引 言
仿真人体下肢的生物动力响应，是生物力学研究的一个重要领域。随着康复工程的发展，临床上要求知道愈来愈多的人体下肢的动力特性。在其他学科，如运动医学、运动员训练、机车设计和伤亡保护等，也都愈来愈关注人体下肢的运动和力的关系。本模型仿真了人体下肢的生物动力运动，并可用来计算人体下肢在冲击外载荷的作用下，下肢的重要承力部位-膝关节处的结构力(包括：膝关节的咬合接触力、膝关节处4个主要韧带张力等)，同时本模型也可用来计算人体下肢在运动期间，膝关节处的咬合位移以及膝关节和髋关节的屈伸位移等。另外，本模型还为研究人工关节、人工韧带以及它们的受伤与重建等提供了一种新的途径。
2 模型方程
2.1 坐标系
, 百拇医药
根据人体下肢解剖结构，建立2个坐标系，即：(x,y)和(x′,y′)坐标系，如图1所示。坐标系(x,y)为固定坐标系，其单位矢量用
表示，被固结在固定体股骨(FEMUR)上；而坐标系(x′,y′)为运动坐标系，其单位矢量表示，被固结在运动体股骨(TIBIA)上。y轴和y′轴分别沿着股骨和胫骨的长骨方向，均指向膝关节；x轴和x′轴分别垂直于长骨，指向如图1所示。为便于与文献结果比较，我们取2个坐标系的原心与文献[1，2]相同。
坐标系(x,y)的原点取在距股骨咬合曲与y轴的交叉点为y=4.01 cm处；而坐标系(x′,y′)的原点取在股骨的质量中心，该点距胫骨咬合曲与y′轴的交叉点为y′=21.34 cm处。这样，运动坐标系(x′,y′)相对于固定坐标系(x,y)的运动，则可用3个量来描述，即(x′,y′)坐标系原心(x′0,y′0)在x和y方向的相对平移分量和它们的相对旋转角θ。对照图1，可获得这2个坐标系之间有如下的旋转变换关系式：
(1)
, 百拇医药
其中：下标F、T分别为固定体股骨和运动体胫骨。
图1 坐标系位置图
Fig 1 Coordinate system
2.2 运动协调约束条件
股骨与胫骨的运动协调约束条件有2个，即运动膝关节股骨与胫骨相咬合时的几何约束条件和运动膝关节股骨与胫骨相咬合时，在接触点C，其2个接触面法向矢量必共线。这2个咬合约束条件给出如下：
(1)运动膝关节股骨与胫骨咬合运动时的几何约束条件为(参见图1)：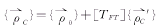
(2)
, 百拇医药
其中：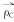
和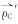
分别为股骨与胫骨接触点C在坐标系(x,y)和坐标系(x′,y′)中的位置矢量，而
则为坐标系(x′,y′)的原点在坐系(x,y)中的位置矢量。
(2)若令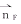
和
分别为股骨咬合曲线与胫骨咬合曲线在接触点C的单位法向矢量。这样，运动膝关节股骨与胫骨咬合时，在接触点C，其2个接触面法向量必共线的条件，则可表示：
，对x=xC和x′=x′C，即：
, 百拇医药
sinθ[1(dfFT/dx)｜X=XC(dfTF/dx′)｜X′=X′C]-
cosθ[1(dfFT/dx)｜X=XC-(dfTF/dx′)｜X′=X′C]=0 (3)
其中：y=fFT(x)和y′=fTF(x′)分别为股骨与胫骨咬合时，股骨和胫骨各自的接触表面方程，其可通过x-ray和数字仪测定并应用最小二乘法拟合而获得。这里，为便于与文献比较，应用Moeinzadeh和Engin等[1]给出的结果。其形式如下：
(4)
, 百拇医药
其中：拟合系数A0～A4和B0～B2分别为：
A0=0.04014018 A1=-0.24762106
A2=-6.8891856A3=-270.4456
A4=-8589.9421
B0=0.21337303B1=-0.04560514
B2=1.09734459
2.3 运动方程
, 百拇医药
分析运动体胫骨的受力状态，知作用在其上的力有：韧带张力
，接触力
，重力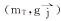
和作用在胫骨质量中心的外载荷
和
(这些外载荷可模拟小腿在任意处受冲击载荷作用或踢球等活动所引起的生物载荷[1，2，4，5])。这样运动体胫骨的运动方程可写为：
(5)
(6)
(7)
, 百拇医药
其中：
为沿着第j个韧带长度方向的单位矢量，其指向由胫骨到股骨；
为第j个韧带插入点在(x′,y′)坐标系中的位置矢量；IT为胫骨的转动惯量。
3 模型参数
由于人体测量学(Anthropometry)是一门非常复杂的学科。它不仅要求能描述和区分人类的种族、性别、年龄、体形等方面的特征；而且就人体运动分析而言，还必须测量诸如质量、质量中心、惯性矩等；另外对于建立解剖基模型，还需测量关节的咬合曲面以及韧带和肌肉的起止位置等。遗憾的是，目前还没有文献报道过1例完整的这类人体数据。本文这部分的数值解所需的模型参数，是基于文献[1～3]，并根据1∶1的解剖图进行适当的调整而获得，以保证这些参数的协调性。这些参数的值已在本文的各部分分别给出。
, http://www.100md.com
3.1 韧带力学模型及人体参数
这里仅考虑膝关节处的4个主要韧带，即前交叉韧带(AC)、反交叉韧带(PC)、外侧副韧带(LC)和内侧副韧带(MC)。韧带的力学模型取自[1，2]，给出如下：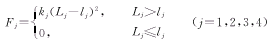
(8)
其中：kj为刚度系数；Lj和lj分别为第j韧带的当前和初始长度。这些参数给出如下[1，2]： 韧带参数
刚度系数kj
(N/mm)
初始长度lj(x,y)
, 百拇医药
(cm)
初始长度lj(x′,y′)
(cm)
前交叉韧带(AC)
30
(-0.6,1.0)
(0.8,17.3)
后交叉韧带(PC)
35
(-1.6,1.0)
(-0.7,17.3)
外侧副韧带(LC)
, 百拇医药
15
(-2.5,0.7)
(2.4,14.5)
内侧副韧带(MC)
15
(-1.2,0.6)
(0,15.5)
人体参数
mT=3.72kg, IT=0.064kg/m2
3.2 外载荷形式
本计算取作用在胫骨质量中心的外载荷形式与Moeinzadeh和Engin等[1]及Eahamn和Hefzy[2]的形式相同，即：为零，而生物撞击型外载荷为两类力函形式，即第一类为矩形力函，第二类则为指数衰减正弦力函，且取
给出如下：
(9)
, 百拇医药
其中：A，
均为力幅；A=0.53
4 数值解技术
对约束协调方程(2)和(3)连续微分两次，这样其与运动控制微分方程(5)～(7)一起共同构成了描述人体小腿在矢状面内的动力响应方程组，这组描述初始值问题的2阶非性微分方程系统，经整理后可写成以下形式：
(10)
其中：[A]为1个6×6系数矩阵；[F1…F5F6]T为时间相关的力矢量。求解未知加速和接触力矢量，则方程(10)可进一步写成：
(11)
, http://www.100md.com
其中：Si为[A]-1[F]T矢量的元素，可由5个位置矢量
及其它们的1阶导数和已知的外力等来表示。这样对方程(11)进行数值积分，即可获得5个位置矢量。然后根据这5个位置矢量及其1阶导数和已知外力等，代入方程(11)的第2部分，即可获得接触力N。我们应用双精度4阶龙格-库塔(Runge-Kutta)法，求解这组初始值问题。数值结果见下节。
5 数值结果与讨论
膝关节接触力与时间的关系图对于上述两类力函，分别如图2和图3所示。结果显示，对于这两类力函，随着外载荷幅值的增大，相应的膝关节接触力也增大。
韧带张力与膝关节运动折叠角θ的关系对于上述两类力函分别如图4和图5所示。结果显示，对于两类力函，由前交叉韧带(AC)所承受的载荷运较其他韧带所承受的载荷要高。
, 百拇医药
图2 接触力与时间的关系图
矩形力函：t0=15s
Fig 2 Contact Forces via Time
Step force function:t0=15s
图3 接触力与时间的关系图
正弦力函：t0=15s
Fig 3 Contact Forces via Time
Sinusoidal force function:tO=15s
, 百拇医药
图4 韧带张力与θ角的关系图
矩形力函：A=60N
Fig 4 Ligament Forces via Flexion Angle
Step force function:A=60N
图5 韧带张力与θ角的关系图
正弦力函:=60N
Fig 5 Ligament Forces via Flexion Angle
, http://www.100md.com Sinusoidal force function:=60N
膝关节股骨与胫骨咬合的接触点位置，以及小腿质量中心的位移对于两类力函则分别如图6和图7所示。由这两图可看出，在接触点的位移曲线上，明显地反映了膝关节股骨与胫骨滚动与滑动的运动咬合。由于篇幅所限，更多的结果不在这里表述。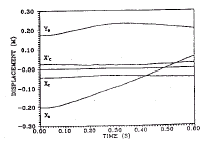
图6 位移与时间的关系图
矩形力函：A=60N
Fig 6 Displacement via Time
Step force function:A=60N
, 百拇医药
图7 位移与时间的关系图
正弦力函：=60N
Fig 7 Displacement via Time
Sinusoidal force function:=60N
6 结束语
我们建立了人体下肢大腿固定而小腿在矢状面内运动时的生物动力响应模型。并计算了当小腿胫骨质量中心遭受两类外载荷作用时，由此而引起的膝关节接触力和膝关节处的4个主要韧带所承受的张力以及膝关节胫骨与股骨咬合的接触点位置、小腿的前后屈伸位移和运动轨迹等。本模型对于临床医学、运动员的训练、伤亡保护以及机车设计等均有着一定的指导意义。另外，本模型还为研究人工关节、人工韧带以及它们的受伤与重建等提供了一种新的途径。
, 百拇医药
河北省自然科学基金资助项目(398152)
参考文献
1，Moeinzadeh MH, Engin AE，Akkas N. Two-dimensional dynamic modeling of human knee joint. ASME, J Biomech, 1983; 16∶253
2，Rahman EA，Hefzy MS. A two-dimensional dynamic anatomical model of the human knee joint, ASME, J Biomech Engr, 1993;115：357
3，Winter DA. Biomechanics of human movement. John Wiley & Sons Publishing Co., New York，1976
, http://www.100md.com
4，Xishi Wang, Two-Dimensional Biodynamic Model of the Human Lower Extremity, Ph. D. Thesis, Middled East Technical University, Ankara, Turkey, 1994
5，S.Turgut Tumer,Wang Xishi, Nuri AKkas, A Planar Dynamic Anatomical Model of the Human Lower Limb, Biomedical Engineering, 1995; 7： 365
6，郭光文，王 序.人体解剖彩色图谱.北京：人民卫生出版社，1995：49-56
(收稿：1998-12-03 修回：1999-07-08), 百拇医药
单位：王西十 白瑞蒲(河北大学 数学系，保定 071002)；S.Turgut Tumer(Department of Mechanical Engineering, Middle East Technical University, Ankara-6531, Turkey)
关键词：人体小腿；冲击载荷；生物动力响应
生物医学工程学杂志000210 摘要 建立了人体下肢大腿固定而小腿在矢状面内运动时的生物动力模型，并对这类数学模型的求解，发展了一种有效且易于使用的解法技术。作为应用，计算了当小腿在胫骨质量中心遭受冲击载荷时，由此而引起的膝关节咬合接触力、膝关节处的4个主要韧带所承受的张力以及膝关节股骨与胫骨咬合时的接触点的位置、小腿的前后屈伸位移和运动轨迹等。
Biodynamic Response of the Human Shank Subjected to Impulse Load
, 百拇医药
Wang Xishi Bai Ruipu
(Department of Mathematics, Hebei University, Baoding 071002)
S.Turgut Tumer
(Department of Mechanical Engineering, Middle East Technical University,Ankara-6531, Turkey)
Abstract This paper reported the establishment of biodynamic modelling of the human shank in the sagittal palne while the human thigh is fixed. And when the shank is subjected to the two types of externally applied impulse loads, the forces associated with the four main ligaments, as well as the bone-to-bone contact forces in the knee joint are numerically obtained. The contact point locations are also presented together with the angular motions of the lower limb segments.
, 百拇医药
Key words Human shank Impulse load Biodynamic response
1 引 言
仿真人体下肢的生物动力响应，是生物力学研究的一个重要领域。随着康复工程的发展，临床上要求知道愈来愈多的人体下肢的动力特性。在其他学科，如运动医学、运动员训练、机车设计和伤亡保护等，也都愈来愈关注人体下肢的运动和力的关系。本模型仿真了人体下肢的生物动力运动，并可用来计算人体下肢在冲击外载荷的作用下，下肢的重要承力部位-膝关节处的结构力(包括：膝关节的咬合接触力、膝关节处4个主要韧带张力等)，同时本模型也可用来计算人体下肢在运动期间，膝关节处的咬合位移以及膝关节和髋关节的屈伸位移等。另外，本模型还为研究人工关节、人工韧带以及它们的受伤与重建等提供了一种新的途径。
2 模型方程
2.1 坐标系
, 百拇医药
根据人体下肢解剖结构，建立2个坐标系，即：(x,y)和(x′,y′)坐标系，如图1所示。坐标系(x,y)为固定坐标系，其单位矢量用
表示，被固结在固定体股骨(FEMUR)上；而坐标系(x′,y′)为运动坐标系，其单位矢量表示，被固结在运动体股骨(TIBIA)上。y轴和y′轴分别沿着股骨和胫骨的长骨方向，均指向膝关节；x轴和x′轴分别垂直于长骨，指向如图1所示。为便于与文献结果比较，我们取2个坐标系的原心与文献[1，2]相同。坐标系(x,y)的原点取在距股骨咬合曲与y轴的交叉点为y=4.01 cm处；而坐标系(x′,y′)的原点取在股骨的质量中心，该点距胫骨咬合曲与y′轴的交叉点为y′=21.34 cm处。这样，运动坐标系(x′,y′)相对于固定坐标系(x,y)的运动，则可用3个量来描述，即(x′,y′)坐标系原心(x′0,y′0)在x和y方向的相对平移分量和它们的相对旋转角θ。对照图1，可获得这2个坐标系之间有如下的旋转变换关系式：
(1), 百拇医药
其中：下标F、T分别为固定体股骨和运动体胫骨。
图1 坐标系位置图
Fig 1 Coordinate system
2.2 运动协调约束条件
股骨与胫骨的运动协调约束条件有2个，即运动膝关节股骨与胫骨相咬合时的几何约束条件和运动膝关节股骨与胫骨相咬合时，在接触点C，其2个接触面法向矢量必共线。这2个咬合约束条件给出如下：
(1)运动膝关节股骨与胫骨咬合运动时的几何约束条件为(参见图1)：
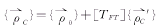(2), 百拇医药
其中：
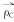和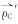分别为股骨与胫骨接触点C在坐标系(x,y)和坐标系(x′,y′)中的位置矢量，而则为坐标系(x′,y′)的原点在坐系(x,y)中的位置矢量。(2)若令
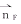和分别为股骨咬合曲线与胫骨咬合曲线在接触点C的单位法向矢量。这样，运动膝关节股骨与胫骨咬合时，在接触点C，其2个接触面法向量必共线的条件，则可表示：，对x=xC和x′=x′C，即：, 百拇医药
sinθ[1(dfFT/dx)｜X=XC(dfTF/dx′)｜X′=X′C]-
cosθ[1(dfFT/dx)｜X=XC-(dfTF/dx′)｜X′=X′C]=0 (3)
其中：y=fFT(x)和y′=fTF(x′)分别为股骨与胫骨咬合时，股骨和胫骨各自的接触表面方程，其可通过x-ray和数字仪测定并应用最小二乘法拟合而获得。这里，为便于与文献比较，应用Moeinzadeh和Engin等[1]给出的结果。其形式如下：
(4), 百拇医药
其中：拟合系数A0～A4和B0～B2分别为：
A0=0.04014018 A1=-0.24762106
A2=-6.8891856A3=-270.4456
A4=-8589.9421
B0=0.21337303B1=-0.04560514
B2=1.09734459
2.3 运动方程
, 百拇医药
分析运动体胫骨的受力状态，知作用在其上的力有：韧带张力
，接触力，重力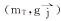和作用在胫骨质量中心的外载荷和(这些外载荷可模拟小腿在任意处受冲击载荷作用或踢球等活动所引起的生物载荷[1，2，4，5])。这样运动体胫骨的运动方程可写为： (5) (6) (7), 百拇医药
其中：
为沿着第j个韧带长度方向的单位矢量，其指向由胫骨到股骨；为第j个韧带插入点在(x′,y′)坐标系中的位置矢量；IT为胫骨的转动惯量。3 模型参数
由于人体测量学(Anthropometry)是一门非常复杂的学科。它不仅要求能描述和区分人类的种族、性别、年龄、体形等方面的特征；而且就人体运动分析而言，还必须测量诸如质量、质量中心、惯性矩等；另外对于建立解剖基模型，还需测量关节的咬合曲面以及韧带和肌肉的起止位置等。遗憾的是，目前还没有文献报道过1例完整的这类人体数据。本文这部分的数值解所需的模型参数，是基于文献[1～3]，并根据1∶1的解剖图进行适当的调整而获得，以保证这些参数的协调性。这些参数的值已在本文的各部分分别给出。
, http://www.100md.com
3.1 韧带力学模型及人体参数
这里仅考虑膝关节处的4个主要韧带，即前交叉韧带(AC)、反交叉韧带(PC)、外侧副韧带(LC)和内侧副韧带(MC)。韧带的力学模型取自[1，2]，给出如下：
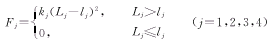(8)其中：kj为刚度系数；Lj和lj分别为第j韧带的当前和初始长度。这些参数给出如下[1，2]： 韧带参数
刚度系数kj
(N/mm)
初始长度lj(x,y)
, 百拇医药
(cm)
初始长度lj(x′,y′)
(cm)
前交叉韧带(AC)
30
(-0.6,1.0)
(0.8,17.3)
后交叉韧带(PC)
35
(-1.6,1.0)
(-0.7,17.3)
外侧副韧带(LC)
, 百拇医药
15
(-2.5,0.7)
(2.4,14.5)
内侧副韧带(MC)
15
(-1.2,0.6)
(0,15.5)
人体参数
mT=3.72kg, IT=0.064kg/m2
3.2 外载荷形式
本计算取作用在胫骨质量中心的外载荷形式与Moeinzadeh和Engin等[1]及Eahamn和Hefzy[2]的形式相同，即：
为零，而生物撞击型外载荷为两类力函形式，即第一类为矩形力函，第二类则为指数衰减正弦力函，且取给出如下： (9), 百拇医药
其中：A，
均为力幅；A=0.534 数值解技术
对约束协调方程(2)和(3)连续微分两次，这样其与运动控制微分方程(5)～(7)一起共同构成了描述人体小腿在矢状面内的动力响应方程组，这组描述初始值问题的2阶非性微分方程系统，经整理后可写成以下形式：
(10)其中：[A]为1个6×6系数矩阵；[F1…F5F6]T为时间相关的力矢量。求解未知加速和接触力矢量，则方程(10)可进一步写成：
(11), http://www.100md.com
其中：Si为[A]-1[F]T矢量的元素，可由5个位置矢量
及其它们的1阶导数和已知的外力等来表示。这样对方程(11)进行数值积分，即可获得5个位置矢量。然后根据这5个位置矢量及其1阶导数和已知外力等，代入方程(11)的第2部分，即可获得接触力N。我们应用双精度4阶龙格-库塔(Runge-Kutta)法，求解这组初始值问题。数值结果见下节。5 数值结果与讨论
膝关节接触力与时间的关系图对于上述两类力函，分别如图2和图3所示。结果显示，对于这两类力函，随着外载荷幅值的增大，相应的膝关节接触力也增大。
韧带张力与膝关节运动折叠角θ的关系对于上述两类力函分别如图4和图5所示。结果显示，对于两类力函，由前交叉韧带(AC)所承受的载荷运较其他韧带所承受的载荷要高。
, 百拇医药
图2 接触力与时间的关系图
矩形力函：t0=15s
Fig 2 Contact Forces via Time
Step force function:t0=15s
图3 接触力与时间的关系图
正弦力函：t0=15s
Fig 3 Contact Forces via Time
Sinusoidal force function:tO=15s
, 百拇医药
图4 韧带张力与θ角的关系图
矩形力函：A=60N
Fig 4 Ligament Forces via Flexion Angle
Step force function:A=60N
图5 韧带张力与θ角的关系图
正弦力函:
=60NFig 5 Ligament Forces via Flexion Angle
, http://www.100md.com Sinusoidal force function:
=60N膝关节股骨与胫骨咬合的接触点位置，以及小腿质量中心的位移对于两类力函则分别如图6和图7所示。由这两图可看出，在接触点的位移曲线上，明显地反映了膝关节股骨与胫骨滚动与滑动的运动咬合。由于篇幅所限，更多的结果不在这里表述。
图6 位移与时间的关系图
矩形力函：A=60N
Fig 6 Displacement via Time
Step force function:A=60N
, 百拇医药
图7 位移与时间的关系图
正弦力函：
=60NFig 7 Displacement via Time
Sinusoidal force function:
=60N6 结束语
我们建立了人体下肢大腿固定而小腿在矢状面内运动时的生物动力响应模型。并计算了当小腿胫骨质量中心遭受两类外载荷作用时，由此而引起的膝关节接触力和膝关节处的4个主要韧带所承受的张力以及膝关节胫骨与股骨咬合的接触点位置、小腿的前后屈伸位移和运动轨迹等。本模型对于临床医学、运动员的训练、伤亡保护以及机车设计等均有着一定的指导意义。另外，本模型还为研究人工关节、人工韧带以及它们的受伤与重建等提供了一种新的途径。
, 百拇医药
河北省自然科学基金资助项目(398152)
参考文献
1，Moeinzadeh MH, Engin AE，Akkas N. Two-dimensional dynamic modeling of human knee joint. ASME, J Biomech, 1983; 16∶253
2，Rahman EA，Hefzy MS. A two-dimensional dynamic anatomical model of the human knee joint, ASME, J Biomech Engr, 1993;115：357
3，Winter DA. Biomechanics of human movement. John Wiley & Sons Publishing Co., New York，1976
, http://www.100md.com
4，Xishi Wang, Two-Dimensional Biodynamic Model of the Human Lower Extremity, Ph. D. Thesis, Middled East Technical University, Ankara, Turkey, 1994
5，S.Turgut Tumer,Wang Xishi, Nuri AKkas, A Planar Dynamic Anatomical Model of the Human Lower Limb, Biomedical Engineering, 1995; 7： 365
6，郭光文，王 序.人体解剖彩色图谱.北京：人民卫生出版社，1995：49-56
(收稿：1998-12-03 修回：1999-07-08), 百拇医药