无限元与有限元区域边界位移值的D—N迭代求解法
作者:辛海涛 马轩祥 耿建平 应隆安 钱宗才 张少峰 吴金彪 齐 春 黄 辉 李 斌
单位:第四军医大学口腔医学院710032
关键词:
无限元与有限元区域边界 位移值的D 无限元法是基于有限元方法之上,将无限剖分思想与有限元方法相结合,在应力、形变等规则区域若使用有限剖分计算可达到精度要求时,则使用有限元法计算,而在形变剧烈、有应力集中的区域则采用无限相似单元剖分的无限元法计算,以求得应力集中区域确切应力分布状况,以弥补有限元法因剖分限制和单元内应力平均和扩散而降底计算精度的不足[1]。同一模型中的无限元与有限元区域的共同边值的计算则采用D—N迭代法。
1 D—N迭代法
1.1基本概念 D—N迭代法是区域分解法的一种,而区域分解法是80年代以来发展起来的一种新的计算方法,是将同一模型根据不同的特点或不同的要求分解成若干个区域,各区域则采用不同的算法,如本实验将模型分为有限元区域和无限元区域,求解整个模型以达到计算目的[2]。由于该方法具有能将大型问题分解成小型问题,将复杂的边值问题转化成简单的边值问题,将串行问题分解成小的并行问题,所以它是目前计算数学的热门领域之一[3]。我们采用D-N迭代法主要计算所划分的无限元区域和有限元区域共同边界的位移和应力值。假设我们讨论的区域为Ω,并将Ω分解成两个子区域,其中Ω1按通常的有限元方法进行剖分,我们称之为有限元区域。Ω2通常取成一个多边形,对其做无限相似单元剖分,我们称无限元区域(区域划分可参考图1。D-N迭代即是有限元区域Ω1交换给无限元区域Ω2第一边值条件(位移条件),而区域Ω2则给区域Ω1第二边界条件(应力条件),从而达到一步步迭代求出最终解的目的。当相邻的两次位移结果之差达到给定的误差限度时既可停止。
, http://www.100md.com
1.2D-N迭代法的具体实现
(1)建立模型Ω并根据实际情况或有限元计算结果将其划分为Ω1区域、Ω2区域。
(2)Ω1区域通过有限元法计算出模型含有位移的数据文件*.L。
(3)将*.L文件做为Ω2的边界条件通过无限元法计算形成FORCE文件。
(4)再将FORCE做为Ω1的边界值,如此反复进行,直到误差达到要求。
2 实例计算
无限元分析系统建立后,我们利用二维柱状牙根骨内种植义齿45℃100N斜向偏心加载模型[4]进行试算(模型简图见图1),对模型中种植体及牙槽骨、牙体组织应力分布变化不大区域用有限元法进行计算,而对根尖孔区域应力集中部位[5]分解为无限元区域进行计算,两区域共同边界值即用D-N迭代法进行,并与单纯使用Super-SAP有限元分析软件所计算的结果加以比较[6],(结果见表1)。同时在共同边界上任选一节点,对其在X轴上位移值进行观察,以分析计算方法的收敛性(结果见图2)。然后我们将边界值引入无限元区域以实例验证边界位移和无限元区域应力计算结果(图4)。同时计算了不同角度下(以O点为原点,OA为极坐标轴,任取角度α)无限元法的应力强度因子,来反映不同材料中断的可能性,并将其数量化,结果见图3。
, 百拇医药
图1 有限元—无限元区域划分示意图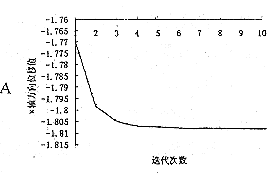
图2 D—N迭代的收敛过程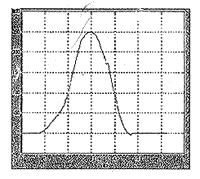
图3 应力强度因子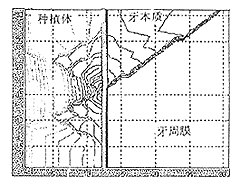
图4 无限元区域应力分布图
表1 D-N迭代无限元法与有限元法求解应力集中
区域边界位移条件的计算结果 节点号
原始坐标值
(mm)
, http://www.100md.com
有限元的位移值
(×10-4cm)
无限元的位移值
(×10-4cm)
横轴
纵轴
横轴
纵轴
横轴
纵轴
85
0.06
, 百拇医药 1.06
-1.82
-1.31
-1.81
-1.31
144
0.09
1.04
-1.64
-0.98
-1.62
-0.99
669
, 百拇医药
0.14
1.08
-1.03
-0.76
-1.01
-0.77
639
0.14
1.12
-2.57
0.17
-2.55
0.19
, http://www.100md.com
146
0.09
1.12
-2.59
-0.78
-2.57
-0.76
86
0.06
1.10
-2.30
-1.25
-2.28
, http://www.100md.com
-1.25
从表1结果可以看出:无限元法D-N迭代所确定的共同边界节点位移值与单纯有限元法仅有较小的差异,最大相差0.254,最小差0.0029,平均为0.066,而且位移值方向一致。较小的差异是无限元与有限元法本身剖分和计算方法不同所致,体现了无限元方法的特点,同时也验证了无限元方法结果的可靠性。从图2中显示的结果可以看出:D-N迭代计算10次后结果即趋于平稳,逐渐收敛于共同边界位移值,表明其收敛速度快,计算效率高、精确度高。由图4可见:柱状根骨内种植义齿右侧根尖孔区域呈现拉应力集中。应力集中点为牙本质、种植体和牙周膜交汇点O,并向周围呈放散状减小。牙本质内越靠近种植体界面和O点应力越增大,结果解释了临床这些部位易发生根折的原因。种植体内部向其界面方向和中心O点应力也逐渐增大。同时从应力强度因子计算结果(图3)可见α=π方向时应力强度因子值最大,表明从O点垂直于种植体界面方向应力最大,中断的可能性也最大。提示临床工作中不能以减小种植体出根尖孔处直径来预防根折发生。3 讨 论
, http://www.100md.com
从实例计算可以看出,无限元法能准确计算出应力集中区域的确切应力分布状况,为临床准确掌握这些区域应力集中趋势提供了具体、逼真的资料,而有限元法计算时因剖分限制和单元内应力平均则不能确切反映出这样的应力分布趋势。应力强度因子的计算也客观反映出材料断裂的可能性,待后续实验确定出材料临界应力强度因子后,就可分析出何种载荷下即可引起断裂,为临床修复体优化设计提供理论依据。而所有这些无限元计算结果都依赖共同边界位移值的计算。它是无限元法得以实现的主要前提条件,同时又是有限元的边界条件。由实例计算可见D-N迭代法能精确计算出共同边界位移值,并且使有限元与无限元法的联接得以实现,它是一种快速、准确的计算共同边值问题的计算方法,而且该方法还能使模型中所划分的多个无限元区域与有限元联接得以实现,从而为解决口腔生物力学分析中因模型复杂多变或存在奇点而难以准确计算的困难带来了希望。
参考文献
1 应隆安.无限元方法.北京:北京大学出版社,1992.1~3
, http://www.100md.com
2 李开泰,黄艾香,黄庆怀. 有限元方法及其应用. 西安:西安交通大学出版社,1992.17~24
3 丁预展. 离散论文方法学. 北京:中国建筑工业出版社,1988.190~200
4 黄 辉,马轩祥,张少锋. 柱状螺旋牙根骨内种植体形态设计的有限元分析:[硕士论文]. 西安:第四军医大学,1996.5
5 Williams KR. A finit element stress analysis of an endodonticlly restored tooth Engineer Med, 1984,13:167
6 张春宝,马轩祥. 根骨内种植体的临床应用和影响因素. 实用口腔医学杂志,1996,12(4):286
(收稿:1998-12-08), http://www.100md.com
单位:第四军医大学口腔医学院710032
关键词:
无限元与有限元区域边界 位移值的D 无限元法是基于有限元方法之上,将无限剖分思想与有限元方法相结合,在应力、形变等规则区域若使用有限剖分计算可达到精度要求时,则使用有限元法计算,而在形变剧烈、有应力集中的区域则采用无限相似单元剖分的无限元法计算,以求得应力集中区域确切应力分布状况,以弥补有限元法因剖分限制和单元内应力平均和扩散而降底计算精度的不足[1]。同一模型中的无限元与有限元区域的共同边值的计算则采用D—N迭代法。
1 D—N迭代法
1.1基本概念 D—N迭代法是区域分解法的一种,而区域分解法是80年代以来发展起来的一种新的计算方法,是将同一模型根据不同的特点或不同的要求分解成若干个区域,各区域则采用不同的算法,如本实验将模型分为有限元区域和无限元区域,求解整个模型以达到计算目的[2]。由于该方法具有能将大型问题分解成小型问题,将复杂的边值问题转化成简单的边值问题,将串行问题分解成小的并行问题,所以它是目前计算数学的热门领域之一[3]。我们采用D-N迭代法主要计算所划分的无限元区域和有限元区域共同边界的位移和应力值。假设我们讨论的区域为Ω,并将Ω分解成两个子区域,其中Ω1按通常的有限元方法进行剖分,我们称之为有限元区域。Ω2通常取成一个多边形,对其做无限相似单元剖分,我们称无限元区域(区域划分可参考图1。D-N迭代即是有限元区域Ω1交换给无限元区域Ω2第一边值条件(位移条件),而区域Ω2则给区域Ω1第二边界条件(应力条件),从而达到一步步迭代求出最终解的目的。当相邻的两次位移结果之差达到给定的误差限度时既可停止。
, http://www.100md.com
1.2D-N迭代法的具体实现
(1)建立模型Ω并根据实际情况或有限元计算结果将其划分为Ω1区域、Ω2区域。
(2)Ω1区域通过有限元法计算出模型含有位移的数据文件*.L。
(3)将*.L文件做为Ω2的边界条件通过无限元法计算形成FORCE文件。
(4)再将FORCE做为Ω1的边界值,如此反复进行,直到误差达到要求。
2 实例计算
无限元分析系统建立后,我们利用二维柱状牙根骨内种植义齿45℃100N斜向偏心加载模型[4]进行试算(模型简图见图1),对模型中种植体及牙槽骨、牙体组织应力分布变化不大区域用有限元法进行计算,而对根尖孔区域应力集中部位[5]分解为无限元区域进行计算,两区域共同边界值即用D-N迭代法进行,并与单纯使用Super-SAP有限元分析软件所计算的结果加以比较[6],(结果见表1)。同时在共同边界上任选一节点,对其在X轴上位移值进行观察,以分析计算方法的收敛性(结果见图2)。然后我们将边界值引入无限元区域以实例验证边界位移和无限元区域应力计算结果(图4)。同时计算了不同角度下(以O点为原点,OA为极坐标轴,任取角度α)无限元法的应力强度因子,来反映不同材料中断的可能性,并将其数量化,结果见图3。

, 百拇医药
图1 有限元—无限元区域划分示意图

图2 D—N迭代的收敛过程

图3 应力强度因子

图4 无限元区域应力分布图
表1 D-N迭代无限元法与有限元法求解应力集中
区域边界位移条件的计算结果 节点号
原始坐标值
(mm)
, http://www.100md.com
有限元的位移值
(×10-4cm)
无限元的位移值
(×10-4cm)
横轴
纵轴
横轴
纵轴
横轴
纵轴
85
0.06
, 百拇医药 1.06
-1.82
-1.31
-1.81
-1.31
144
0.09
1.04
-1.64
-0.98
-1.62
-0.99
669
, 百拇医药
0.14
1.08
-1.03
-0.76
-1.01
-0.77
639
0.14
1.12
-2.57
0.17
-2.55
0.19
, http://www.100md.com
146
0.09
1.12
-2.59
-0.78
-2.57
-0.76
86
0.06
1.10
-2.30
-1.25
-2.28
, http://www.100md.com
-1.25
从表1结果可以看出:无限元法D-N迭代所确定的共同边界节点位移值与单纯有限元法仅有较小的差异,最大相差0.254,最小差0.0029,平均为0.066,而且位移值方向一致。较小的差异是无限元与有限元法本身剖分和计算方法不同所致,体现了无限元方法的特点,同时也验证了无限元方法结果的可靠性。从图2中显示的结果可以看出:D-N迭代计算10次后结果即趋于平稳,逐渐收敛于共同边界位移值,表明其收敛速度快,计算效率高、精确度高。由图4可见:柱状根骨内种植义齿右侧根尖孔区域呈现拉应力集中。应力集中点为牙本质、种植体和牙周膜交汇点O,并向周围呈放散状减小。牙本质内越靠近种植体界面和O点应力越增大,结果解释了临床这些部位易发生根折的原因。种植体内部向其界面方向和中心O点应力也逐渐增大。同时从应力强度因子计算结果(图3)可见α=π方向时应力强度因子值最大,表明从O点垂直于种植体界面方向应力最大,中断的可能性也最大。提示临床工作中不能以减小种植体出根尖孔处直径来预防根折发生。3 讨 论
, http://www.100md.com
从实例计算可以看出,无限元法能准确计算出应力集中区域的确切应力分布状况,为临床准确掌握这些区域应力集中趋势提供了具体、逼真的资料,而有限元法计算时因剖分限制和单元内应力平均则不能确切反映出这样的应力分布趋势。应力强度因子的计算也客观反映出材料断裂的可能性,待后续实验确定出材料临界应力强度因子后,就可分析出何种载荷下即可引起断裂,为临床修复体优化设计提供理论依据。而所有这些无限元计算结果都依赖共同边界位移值的计算。它是无限元法得以实现的主要前提条件,同时又是有限元的边界条件。由实例计算可见D-N迭代法能精确计算出共同边界位移值,并且使有限元与无限元法的联接得以实现,它是一种快速、准确的计算共同边值问题的计算方法,而且该方法还能使模型中所划分的多个无限元区域与有限元联接得以实现,从而为解决口腔生物力学分析中因模型复杂多变或存在奇点而难以准确计算的困难带来了希望。
参考文献
1 应隆安.无限元方法.北京:北京大学出版社,1992.1~3
, http://www.100md.com
2 李开泰,黄艾香,黄庆怀. 有限元方法及其应用. 西安:西安交通大学出版社,1992.17~24
3 丁预展. 离散论文方法学. 北京:中国建筑工业出版社,1988.190~200
4 黄 辉,马轩祥,张少锋. 柱状螺旋牙根骨内种植体形态设计的有限元分析:[硕士论文]. 西安:第四军医大学,1996.5
5 Williams KR. A finit element stress analysis of an endodonticlly restored tooth Engineer Med, 1984,13:167
6 张春宝,马轩祥. 根骨内种植体的临床应用和影响因素. 实用口腔医学杂志,1996,12(4):286
(收稿:1998-12-08), http://www.100md.com