用区组和分层改进简单随机
作者:张学中
单位:军事医学科学院一所,北京 100850
关键词:
中国新药杂志001007
[中图分类号]R969.4 [文献标识码] B
[文章编号]1003-3734(2000)10-0683-04
在ICH-E9[1]中,用很大篇幅说明临床试验研究中随机化各种问题,8次提到区 组,12次提到分层。在国际药品协会(DIA)的权威性刊物Drug Information Journal发布的 与GCP有关的文章里[2,3],也提到了这类问题。本文介绍与此有关的概念,而且讲 述可供实际应用的区组和分层等有限制的随机分组方法。
, http://www.100md.com
1 名词的界定
本文和有关文献中反复提到下列几个名词,从某种意义上说是专业术语,但在一些 统计教学/参考书中常有混淆,有必要在这里首先提出来作简要说明。
简单随机(simple randomization):亦称完全随机,是指靠掷硬币或随机数表,或用计算 机产生随机数来进行随机化,不加任何限制和干预。
有限制的随机(restricted, constrained randomization ):对随机化加以限制,不 是完全随机,是一定条件下的随机。
平衡(balance):主要是指可比较的两组或多组中,各组的受试对象数或所作的处理数相 等。注意与“均衡”区别。
区组(blocking):是对受试对象进行的划分。
, 百拇医药
区组大小或区组长度(size,length):是指一个区组包含多少个接受不同处理的受试 单元。
分层(stratifying):将总体按某(些)特征分割为次级总体。
预后因素(prognostic factor):是临床试验研究中有实际意义的协变量,它可作为 分层的依据。
2 简单随机可能产生不平衡
将N个受试对象,按照简单随机,分配到A,B两个处理组,每个对象可能被分到任一组 的概率为P=0.5。分配完成后,两组数目可能不等。如此作随机安排,刚好两组数目相 等的概率为:
它可能很小,例如,当N=100,每组刚好50个受试对象的概率仅为8%。估价等于或大 于某个特定大小的不平衡情况的概率是包含很多信息的。利用二项分布特性,分到两组中每 一组的期望数目为:
, 百拇医药
E{NA}= E{NB}=NP
这一数目的方差为:
Var{NA}=Var{NB}=NP(1-P)
当N=100和P=1/2,NA的方差为25,近似95%分组数目置信带(bound)为: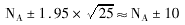
这样一来,我们就会期望比60或40更为不平衡而有利于A(或B)的情况占简单随机的5%。
当我们必须考虑有影响的预后因素时,不平衡的问题更加值得注意,甚至当处理分配的 数目是平衡的,预后因素的分布也是不平衡的。例如,假定有K个独立的二值预后变量,每 个有0.5的概率是“阳性”。比较时I型错误取5%,任何一个变量是平衡的概率则是0.95,所 有K个因素都平衡的概率是 0.95K(假定是独立的)。因而,至少发现有1个因素不平衡 概率为1-0.95K ,当K=5,至少有1个因素在统计上显著不平衡的概率为0.23。
, 百拇医药
3 有约束的随机化
3.1 区组改进平衡 区组随机,是将随机加以约束,使各处理的分配更加平 衡,满足研究要求。在一个区组内包含一个预定的处理分组数目和比例。一个区组的大小必 须是处理组数的整数倍。一区组系列是由随机数字表安排构成的,每一区组内各处理的次序 是随机安排的,但在每一区组内是严格平衡的。考虑两个处理组A和B,实现区组大小为NA +NB的约束借助分配处理A的概率: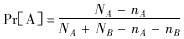 (1)
(1)
当在一个区组内实现了NA次分配,nA= NA,于是再取A的概率为零,当NB次分 配完成,nB= NB,则再取A的概率为1,这是一计算机产生区组安排的实用方法,为做出每一新安排,我们比较一随机数u与概率Pr[A],如果u≤Pr[A]就安排A,使n A加1,否则安排B,使nB加1,u在(0,1)内均匀分布。
, 百拇医药
如果处理数为2,A和B,采用大小为4的区组,则可能共有6种不同的分配(表1)。
表1 区组大小为4的两处理试验的可能配置 区组处理编号
区 组配置编号
1
2
3
4
5
6
1
A
A
, 百拇医药
A
B
B
B
2
A
B
B
B
A
A
3
B
A
, http://www.100md.com
B
A
B
A
4
B
B
A
A
A
B
实验的分配处理的方案是由随机产生的一系列区组构成。如果我们的试验以一个区 组的一半停止,恰巧这一半是两个A,那么就会出现不平衡:多出两个A来。这说明区组引起 的不平衡所产生的情况可能是区组大小的一半。
, http://www.100md.com
在小区组内可能包含的处理的排列数不大。假设有2个处理,区组大小是2b,那么,在 区组内就有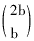 种不同的分配。如果试验严格是在一个区组的一半,多 余的分配数不超过b。多于2个处理时用多项式系数算得可能的配置数。
种不同的分配。如果试验严格是在一个区组的一半,多 余的分配数不超过b。多于2个处理时用多项式系数算得可能的配置数。
实际随机化分组时,所有区组不一定有相同的大小。随机改变区组的长度,两处理用2,4, 6,...;三处理用3,6,9,...。
如果是用随机数字表,表1实际上是这样把随机的数字与区组的处理挂钩的,见表2。表2 区组的随机安排 随机数字
区组内的处理
1
AABB
2
, 百拇医药
ABAB
3
ABBA
4
BBAA
5
BABA
6
BAAB
0,7~9
不用
这样一来,随机数字如为0,5,2,7,8,4,3,7……
对病人安排处理:
, http://www.100md.com
-BABA ABAB--BBAA ABBA-……
3.2 用区组和分层来平衡预后因素 为平衡在临床上重要的预后因素,可以同时用区组和分层随机化。预后因素每个组合构 成一个分立的层,每一层内又进行区组化。在每一层内,所分配的各处理是平衡的;对于每 一处理,各预后因素也是平衡的。
每个病人接受下一个处理安排是从一个特定层配置中找到的,适合某层的她(他) 入选,各层不必以同一速率填满。在一个有区组又分层随机方案中,可能所有各层都填了一 半,即都有A(或B)待填。每个处理中有b个分配,区组大小为2b,层数为k,最大不平衡为k b。换句话说,每层都可能多出b个分配。
对2个处理,4层,区组大小为4,如表3.2的例子,最大不平衡数为8,以不平衡数为8而有利 一种处理或另一种处理的机会为: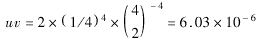
, 百拇医药
而不平衡数少的机会就要大些。u,v的意义为:u为每层仅停于一半的机会;v为所有k个区组 具有同一分配的机会: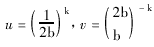
3.3 关于区组和分层问题的其他考虑 如果每一个病人都因有许多预后变量而属于特有的一层,其结果就相当于简单随机。这时 就要少分几层,与处理的数目要相当。换言之,大多数区组应该填满,因为未填满都带来分 配的不平衡。区组大小太大,它将抵销区组的平衡效果,以一个大区组进行处理分配实质是 简单随机,除非到区组的终了附近。例如对公式(1),当NA和NB都很大,对所有分配 好的情况而言,Pr[A]≈1/2。区组可用于不等的分配,例如NA∶NB=2∶1,这时区组 大小应为3的倍数,2/3分配给处理A。
每一病人进入临床研究,须认定应属于哪一层,从相应的随机数表中得到随机的处 理安排。当有多个层时,区组宜小一些。虽然实际问题都可以有多个协变量,但应抓住主要 矛盾,最好只有一个分层因素。
, 百拇医药
3.4 实例 乳腺癌治疗研究中,有两个预后因素较重要:阳 性淋巴结数和年龄。年龄的重要性不仅年长者其生存时间因而短,这与本病无关,而且辅助 化疗也可能与年龄有关。患者这两个预后因素作为协变量,一般是连续变量,但在我们这个 实际情况下,每个变量都可归结为两个值,即年龄<50岁或≥50岁;阳性淋巴结数:1~3个 或4个(以上)。因此,可以把乳腺癌患者按协变量分为4层:①?年龄<50岁和阳性淋巴结数1 ~3个;②?年龄<50岁和阳性淋巴结数≥4个;③? 年龄≥50岁和阳性淋巴结数1~ 3个;④?年龄≥50岁和阳性淋巴结数≥4个。
在试验开始前,准备4份互相独立的随机数字表,每层1个,分别按有约束随机区组 安排各层,与前面的叙述是一样的。如果区组大小为4,两个处理分别是A=噻替派和B=安慰 剂, 所得安排如表3。
表3 乳腺癌患者分层区组随机安排实例 区组
阳性淋巴结 数1~3个
, 百拇医药
阳性淋巴结数4个
<50
≥50
<50
≥50
1
B
B
A
B
A
B
A
A
, 百拇医药
B
A
B
A
A
A
B
B
2
A
A
B
A
B
, 百拇医药
A
A
B
A
B
B
B
B
B
A
A
3
A
B
, http://www.100md.com
B
B
B
A
A
B
B
A
B
A
A
B
A
A
, 百拇医药
4
B
A
B
A
B
B
A
B
A
B
A
A
A
, 百拇医药
A
B
B
4 变通随机化
变通随机化是一个过程,在这一过程中,分到一项临床试验的处理的概率不是常数,但 它却是由现在的平衡状况和/或分组情况来决定。从某种意义上说,区组随机也是这种性质 。但是对于数目平衡,预后变量,分组风险的构成或结果而言更为一般化,详细说明见有关 文献[6]。变通的处理分配有两种类型:有偏投币随机(Biassed Coin Method,Urn Design)和不平衡最小化方法(minimization)。
4.1 有偏投币随机改进平衡 这里只介绍该方法最简单的情形。设想一壶里有1个白球1个红球。如果随机选了红球 分配处理A,则白球为B。第1次选的是红球,其概率为1/2,把红球放回后,再补1个白球 ;在第2次随机摸出前就有3球:1红2白,这样第2次摸到红球的概率为1/3,而白球为2/3, 如此等等,每次都加入1个与所摸到的球相反颜色的球。设NA和NB分别为现在壶内的红 球和白球数(本次摸球前),nA和nB分别为本次及以前摸到过的红球和白球总数。当摸 出过的球数少时,更加有利于趋向平衡,此数目增加得较大后,加入1球已无碍比数大致为1 ∶1,每一次分配的概率都是近似1/2,这方法亦可用于分层分配上。
, http://www.100md.com
此方法用于样本小和需快速平衡的情形,表4为两处理组、两层序贯。
表4 分层的有偏投币随机模型安排处理 分层1
分层2
NA
NB
nA
nB
Pr(A)
处理
NA
NB
, 百拇医药
nA
nB
Pr(A)
处理
1
1
1
0
1/2
A
1
1
1
, 百拇医药
0
1/2
A
1
2
1
1
1/3
B
1
2
1
1
1/3
, 百拇医药
B
2
2
2
1
2/4
A
2
2
1
2
2/4
B
2
, 百拇医药
3
3
1
2/5
A
3
2
1
3
3/5
B
2
4
4
, 百拇医药
1
2/6
A
4
2
1
4
4/6
B
2
5
4
2
2/7
, 百拇医药
B
5
2
2
4
5/7
A
3
5
5
2
3/8
A
5
, http://www.100md.com
3
3
4
5/8
A
3
6
5
3
3/9
B
5
4
4
, http://www.100md.com
4
5/9
A
4
6
5
4
4/10
B
5
5
4
5
5/10
, 百拇医药
B
5
6
5
5
5/11
A
6
5
5
5
6/11
A
5
, 百拇医药
7
6
5
5/12
A
6
6
5
6
6/12
B
5
8
7
, http://www.100md.com
5
5/13
A
7
6
6
6
7/13
A
5
9
8
5
5/14
, 百拇医药
B
7
7
6
7
7/14
B
6
9
8
6
6/15
B
8
, 百拇医药
7P
7
7
8/15
A
7
9
8
7
7/16
B
8
8
7
, 百拇医药
8
8/16
B
8
9
8
8
8/17
A
9
8
7
9
9/17
, 百拇医药
B
8
10
9
4
8/18
A
10
8
7
10
10/18
B
8
, http://www.100md.com
11
10
4
8/19
B
11
8
8
10
11/19
A
9
11
10
, 百拇医药
9
9/20
A
11
9
8
11
11/20
B
9
12
11
9
9/21
, 百拇医药
B
12
9
9
11
12/21
A
4.2 序贯分配处理--不平衡最小化 见表5。表5列出4因 素,各因素水平分别为2,2,2,3。这样一来,共有2×2×2×3=24层。其中有7层无病人 ,最多一层有13个病人,有5层只1个病人,有12层是奇数病人,按层随机就有可能使两种处 理的分配是34∶46,显然,层数多时用“有约束随机区组安排”也会产生很严重的不平衡, 这时可用“不平衡最小化分配方法”,见表6。假设80位病人已经按表6安排好,表内每因素 的各水平病人数之和都是80,现有第81个病人,其4个因素的水平分别是功能状态;能行动 ;年龄(岁):<50;无病期间 (年):≥2;主要转移损害:内脏。满足该因素-水平组合的病 人在表6中以↑表示。在前80位病人中,这类病人接受处理A的和为S1=30+18+9+19=76 ;这类病人接受处理B的和为S2=31+17+8+21=77。因为S1[7],称为“序贯平衡”。表5 乳腺癌晚期患者按层分布 功能状态
, 百拇医药
能行动
不能行动
年龄(岁)
<50
≥50
<50
≥50
无糖生存期间(岁)
<2
≥2
<2
≥2
<2
, 百拇医药
≥2
<2
≥2
主要转移损害
内赃
13
1
9
5
3
1
7
1
骨骼
, 百拇医药
6
0
4
0
0
0
4
1
软组织
8
1
7
7
2
, http://www.100md.com
0
0
0
表6 80位乳腺癌晚期患者按4种病人因素的处理分配 因 素
水 平
处 理
下一病人
A
B
功能状态
能行动
30
31
, http://www.100md.com
↑
不能行动
10
9
年龄(岁)
<50
18
17
↑
≥50
22
23
无病生存期间(岁)
, 百拇医药
<2
31
32
≥2
9
8
↑
主要转移损害
内脏
19
21
↑
骨骼
8
, http://www.100md.com
7
软组织
13
12
4.3 胜者优先 在临床研究中,可采用胜者优先(play the winner)的随机方法以减少接受较差处理的病人数目。首先假定两种处理与壶中两种球 在逻辑上是等价的,作可放回抽样,抽A或B的机会相等。 如果第一个病人随机地分到A而失败了,在壶中就加一个B球;否则加一个A球。这样就会使 接受较好处理方案的病人的机会逐渐愈来愈大;如果两方案是等效的,则分配的概率也近似 相等。实现这种分配方案要求对每个对象都能在评价其处理效果好坏以后再对下一病人分配 试验方案。这一点可能不是总能轻易做到的,一个更为灵活的方法是多阶段设计,对分配比 进行调整,使之有利于本阶段表现得好的一翼。本方法亦适用于结果非二值的情形。一些研 究人员认为这样设计的试验对病人和公益监督委员会(IRB)更为有益。
, 百拇医药
[作者简介] 张学中(1938-),男,教授。研究方向:药品临床试 验统计方法,实验设计与分析。联系电话:(010)68220831。
[参考文献]
[1] E9 Statistical Principles for Clinical Trials[S/OL],http://www. fda.gov/cder/guidance/index.htm,Effective September 16, 1998.
[2] North PM.Ensuring good statistical practice in clinical research:cuidelin es for standard operating procedures(an update),Drug Inf J,1998,32∶665-682.
[3] Marc Buyse.Randomized designs for early trials of new cancer treatments-a n overview[J].Drug Inf J,2000,34∶387-396.
, 百拇医药
[4] Pocock SJ.Clinical trials,a practical approach[M].John Wiley & Son s Ltd.1983,66-89.
[5] Steven Piantadosi.Clinical trials,a methodologic Perspective[M ].New York :John Wiley & Sons,1997.203-229.
[6] Hoel,DG,Sobel M,Weiss GH.A survey of adaptive sampling for clinical t rials[M]. In: RM. Elashoff (Ed.), Perspectives in Biometrics. New York: Acade mic Press,1975.
[7] 汤旦林.医学统计学基础[M].北京:人民卫生出版社,1989.25-27.
收稿:s, 百拇医药
单位:军事医学科学院一所,北京 100850
关键词:
中国新药杂志001007
[中图分类号]R969.4 [文献标识码] B
[文章编号]1003-3734(2000)10-0683-04
在ICH-E9[1]中,用很大篇幅说明临床试验研究中随机化各种问题,8次提到区 组,12次提到分层。在国际药品协会(DIA)的权威性刊物Drug Information Journal发布的 与GCP有关的文章里[2,3],也提到了这类问题。本文介绍与此有关的概念,而且讲 述可供实际应用的区组和分层等有限制的随机分组方法。
, http://www.100md.com
1 名词的界定
本文和有关文献中反复提到下列几个名词,从某种意义上说是专业术语,但在一些 统计教学/参考书中常有混淆,有必要在这里首先提出来作简要说明。
简单随机(simple randomization):亦称完全随机,是指靠掷硬币或随机数表,或用计算 机产生随机数来进行随机化,不加任何限制和干预。
有限制的随机(restricted, constrained randomization ):对随机化加以限制,不 是完全随机,是一定条件下的随机。
平衡(balance):主要是指可比较的两组或多组中,各组的受试对象数或所作的处理数相 等。注意与“均衡”区别。
区组(blocking):是对受试对象进行的划分。
, 百拇医药
区组大小或区组长度(size,length):是指一个区组包含多少个接受不同处理的受试 单元。
分层(stratifying):将总体按某(些)特征分割为次级总体。
预后因素(prognostic factor):是临床试验研究中有实际意义的协变量,它可作为 分层的依据。
2 简单随机可能产生不平衡
将N个受试对象,按照简单随机,分配到A,B两个处理组,每个对象可能被分到任一组 的概率为P=0.5。分配完成后,两组数目可能不等。如此作随机安排,刚好两组数目相 等的概率为:

它可能很小,例如,当N=100,每组刚好50个受试对象的概率仅为8%。估价等于或大 于某个特定大小的不平衡情况的概率是包含很多信息的。利用二项分布特性,分到两组中每 一组的期望数目为:
, 百拇医药
E{NA}= E{NB}=NP
这一数目的方差为:
Var{NA}=Var{NB}=NP(1-P)
当N=100和P=1/2,NA的方差为25,近似95%分组数目置信带(bound)为:
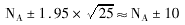
这样一来,我们就会期望比60或40更为不平衡而有利于A(或B)的情况占简单随机的5%。
当我们必须考虑有影响的预后因素时,不平衡的问题更加值得注意,甚至当处理分配的 数目是平衡的,预后因素的分布也是不平衡的。例如,假定有K个独立的二值预后变量,每 个有0.5的概率是“阳性”。比较时I型错误取5%,任何一个变量是平衡的概率则是0.95,所 有K个因素都平衡的概率是 0.95K(假定是独立的)。因而,至少发现有1个因素不平衡 概率为1-0.95K ,当K=5,至少有1个因素在统计上显著不平衡的概率为0.23。
, 百拇医药
3 有约束的随机化
3.1 区组改进平衡 区组随机,是将随机加以约束,使各处理的分配更加平 衡,满足研究要求。在一个区组内包含一个预定的处理分组数目和比例。一个区组的大小必 须是处理组数的整数倍。一区组系列是由随机数字表安排构成的,每一区组内各处理的次序 是随机安排的,但在每一区组内是严格平衡的。考虑两个处理组A和B,实现区组大小为NA +NB的约束借助分配处理A的概率:
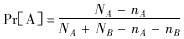 (1)
(1)当在一个区组内实现了NA次分配,nA= NA,于是再取A的概率为零,当NB次分 配完成,nB= NB,则再取A的概率为1,这是一计算机产生区组安排的实用方法,为做出每一新安排,我们比较一随机数u与概率Pr[A],如果u≤Pr[A]就安排A,使n A加1,否则安排B,使nB加1,u在(0,1)内均匀分布。
, 百拇医药
如果处理数为2,A和B,采用大小为4的区组,则可能共有6种不同的分配(表1)。
表1 区组大小为4的两处理试验的可能配置 区组处理编号
区 组配置编号
1
2
3
4
5
6
1
A
A
, 百拇医药
A
B
B
B
2
A
B
B
B
A
A
3
B
A
, http://www.100md.com
B
A
B
A
4
B
B
A
A
A
B
实验的分配处理的方案是由随机产生的一系列区组构成。如果我们的试验以一个区 组的一半停止,恰巧这一半是两个A,那么就会出现不平衡:多出两个A来。这说明区组引起 的不平衡所产生的情况可能是区组大小的一半。
, http://www.100md.com
在小区组内可能包含的处理的排列数不大。假设有2个处理,区组大小是2b,那么,在 区组内就有
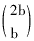 种不同的分配。如果试验严格是在一个区组的一半,多 余的分配数不超过b。多于2个处理时用多项式系数算得可能的配置数。
种不同的分配。如果试验严格是在一个区组的一半,多 余的分配数不超过b。多于2个处理时用多项式系数算得可能的配置数。实际随机化分组时,所有区组不一定有相同的大小。随机改变区组的长度,两处理用2,4, 6,...;三处理用3,6,9,...。
如果是用随机数字表,表1实际上是这样把随机的数字与区组的处理挂钩的,见表2。表2 区组的随机安排 随机数字
区组内的处理
1
AABB
2
, 百拇医药
ABAB
3
ABBA
4
BBAA
5
BABA
6
BAAB
0,7~9
不用
这样一来,随机数字如为0,5,2,7,8,4,3,7……
对病人安排处理:
, http://www.100md.com
-BABA ABAB--BBAA ABBA-……
3.2 用区组和分层来平衡预后因素 为平衡在临床上重要的预后因素,可以同时用区组和分层随机化。预后因素每个组合构 成一个分立的层,每一层内又进行区组化。在每一层内,所分配的各处理是平衡的;对于每 一处理,各预后因素也是平衡的。
每个病人接受下一个处理安排是从一个特定层配置中找到的,适合某层的她(他) 入选,各层不必以同一速率填满。在一个有区组又分层随机方案中,可能所有各层都填了一 半,即都有A(或B)待填。每个处理中有b个分配,区组大小为2b,层数为k,最大不平衡为k b。换句话说,每层都可能多出b个分配。
对2个处理,4层,区组大小为4,如表3.2的例子,最大不平衡数为8,以不平衡数为8而有利 一种处理或另一种处理的机会为:
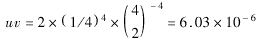
, 百拇医药
而不平衡数少的机会就要大些。u,v的意义为:u为每层仅停于一半的机会;v为所有k个区组 具有同一分配的机会:
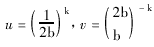
3.3 关于区组和分层问题的其他考虑 如果每一个病人都因有许多预后变量而属于特有的一层,其结果就相当于简单随机。这时 就要少分几层,与处理的数目要相当。换言之,大多数区组应该填满,因为未填满都带来分 配的不平衡。区组大小太大,它将抵销区组的平衡效果,以一个大区组进行处理分配实质是 简单随机,除非到区组的终了附近。例如对公式(1),当NA和NB都很大,对所有分配 好的情况而言,Pr[A]≈1/2。区组可用于不等的分配,例如NA∶NB=2∶1,这时区组 大小应为3的倍数,2/3分配给处理A。
每一病人进入临床研究,须认定应属于哪一层,从相应的随机数表中得到随机的处 理安排。当有多个层时,区组宜小一些。虽然实际问题都可以有多个协变量,但应抓住主要 矛盾,最好只有一个分层因素。
, 百拇医药
3.4 实例 乳腺癌治疗研究中,有两个预后因素较重要:阳 性淋巴结数和年龄。年龄的重要性不仅年长者其生存时间因而短,这与本病无关,而且辅助 化疗也可能与年龄有关。患者这两个预后因素作为协变量,一般是连续变量,但在我们这个 实际情况下,每个变量都可归结为两个值,即年龄<50岁或≥50岁;阳性淋巴结数:1~3个 或4个(以上)。因此,可以把乳腺癌患者按协变量分为4层:①?年龄<50岁和阳性淋巴结数1 ~3个;②?年龄<50岁和阳性淋巴结数≥4个;③? 年龄≥50岁和阳性淋巴结数1~ 3个;④?年龄≥50岁和阳性淋巴结数≥4个。
在试验开始前,准备4份互相独立的随机数字表,每层1个,分别按有约束随机区组 安排各层,与前面的叙述是一样的。如果区组大小为4,两个处理分别是A=噻替派和B=安慰 剂, 所得安排如表3。
表3 乳腺癌患者分层区组随机安排实例 区组
阳性淋巴结 数1~3个
, 百拇医药
阳性淋巴结数4个
<50
≥50
<50
≥50
1
B
B
A
B
A
B
A
A
, 百拇医药
B
A
B
A
A
A
B
B
2
A
A
B
A
B
, 百拇医药
A
A
B
A
B
B
B
B
B
A
A
3
A
B
, http://www.100md.com
B
B
B
A
A
B
B
A
B
A
A
B
A
A
, 百拇医药
4
B
A
B
A
B
B
A
B
A
B
A
A
A
, 百拇医药
A
B
B
4 变通随机化
变通随机化是一个过程,在这一过程中,分到一项临床试验的处理的概率不是常数,但 它却是由现在的平衡状况和/或分组情况来决定。从某种意义上说,区组随机也是这种性质 。但是对于数目平衡,预后变量,分组风险的构成或结果而言更为一般化,详细说明见有关 文献[6]。变通的处理分配有两种类型:有偏投币随机(Biassed Coin Method,Urn Design)和不平衡最小化方法(minimization)。
4.1 有偏投币随机改进平衡 这里只介绍该方法最简单的情形。设想一壶里有1个白球1个红球。如果随机选了红球 分配处理A,则白球为B。第1次选的是红球,其概率为1/2,把红球放回后,再补1个白球 ;在第2次随机摸出前就有3球:1红2白,这样第2次摸到红球的概率为1/3,而白球为2/3, 如此等等,每次都加入1个与所摸到的球相反颜色的球。设NA和NB分别为现在壶内的红 球和白球数(本次摸球前),nA和nB分别为本次及以前摸到过的红球和白球总数。当摸 出过的球数少时,更加有利于趋向平衡,此数目增加得较大后,加入1球已无碍比数大致为1 ∶1,每一次分配的概率都是近似1/2,这方法亦可用于分层分配上。
, http://www.100md.com
此方法用于样本小和需快速平衡的情形,表4为两处理组、两层序贯。
表4 分层的有偏投币随机模型安排处理 分层1
分层2
NA
NB
nA
nB
Pr(A)
处理
NA
NB
, 百拇医药
nA
nB
Pr(A)
处理
1
1
1
0
1/2
A
1
1
1
, 百拇医药
0
1/2
A
1
2
1
1
1/3
B
1
2
1
1
1/3
, 百拇医药
B
2
2
2
1
2/4
A
2
2
1
2
2/4
B
2
, 百拇医药
3
3
1
2/5
A
3
2
1
3
3/5
B
2
4
4
, 百拇医药
1
2/6
A
4
2
1
4
4/6
B
2
5
4
2
2/7
, 百拇医药
B
5
2
2
4
5/7
A
3
5
5
2
3/8
A
5
, http://www.100md.com
3
3
4
5/8
A
3
6
5
3
3/9
B
5
4
4
, http://www.100md.com
4
5/9
A
4
6
5
4
4/10
B
5
5
4
5
5/10
, 百拇医药
B
5
6
5
5
5/11
A
6
5
5
5
6/11
A
5
, 百拇医药
7
6
5
5/12
A
6
6
5
6
6/12
B
5
8
7
, http://www.100md.com
5
5/13
A
7
6
6
6
7/13
A
5
9
8
5
5/14
, 百拇医药
B
7
7
6
7
7/14
B
6
9
8
6
6/15
B
8
, 百拇医药
7P
7
7
8/15
A
7
9
8
7
7/16
B
8
8
7
, 百拇医药
8
8/16
B
8
9
8
8
8/17
A
9
8
7
9
9/17
, 百拇医药
B
8
10
9
4
8/18
A
10
8
7
10
10/18
B
8
, http://www.100md.com
11
10
4
8/19
B
11
8
8
10
11/19
A
9
11
10
, 百拇医药
9
9/20
A
11
9
8
11
11/20
B
9
12
11
9
9/21
, 百拇医药
B
12
9
9
11
12/21
A
4.2 序贯分配处理--不平衡最小化 见表5。表5列出4因 素,各因素水平分别为2,2,2,3。这样一来,共有2×2×2×3=24层。其中有7层无病人 ,最多一层有13个病人,有5层只1个病人,有12层是奇数病人,按层随机就有可能使两种处 理的分配是34∶46,显然,层数多时用“有约束随机区组安排”也会产生很严重的不平衡, 这时可用“不平衡最小化分配方法”,见表6。假设80位病人已经按表6安排好,表内每因素 的各水平病人数之和都是80,现有第81个病人,其4个因素的水平分别是功能状态;能行动 ;年龄(岁):<50;无病期间 (年):≥2;主要转移损害:内脏。满足该因素-水平组合的病 人在表6中以↑表示。在前80位病人中,这类病人接受处理A的和为S1=30+18+9+19=76 ;这类病人接受处理B的和为S2=31+17+8+21=77。因为S1
, 百拇医药
能行动
不能行动
年龄(岁)
<50
≥50
<50
≥50
无糖生存期间(岁)
<2
≥2
<2
≥2
<2
, 百拇医药
≥2
<2
≥2
主要转移损害
内赃
13
1
9
5
3
1
7
1
骨骼
, 百拇医药
6
0
4
0
0
0
4
1
软组织
8
1
7
7
2
, http://www.100md.com
0
0
0
表6 80位乳腺癌晚期患者按4种病人因素的处理分配 因 素
水 平
处 理
下一病人
A
B
功能状态
能行动
30
31
, http://www.100md.com
↑
不能行动
10
9
年龄(岁)
<50
18
17
↑
≥50
22
23
无病生存期间(岁)
, 百拇医药
<2
31
32
≥2
9
8
↑
主要转移损害
内脏
19
21
↑
骨骼
8
, http://www.100md.com
7
软组织
13
12
4.3 胜者优先 在临床研究中,可采用胜者优先(play the winner)的随机方法以减少接受较差处理的病人数目。首先假定两种处理与壶中两种球 在逻辑上是等价的,作可放回抽样,抽A或B的机会相等。 如果第一个病人随机地分到A而失败了,在壶中就加一个B球;否则加一个A球。这样就会使 接受较好处理方案的病人的机会逐渐愈来愈大;如果两方案是等效的,则分配的概率也近似 相等。实现这种分配方案要求对每个对象都能在评价其处理效果好坏以后再对下一病人分配 试验方案。这一点可能不是总能轻易做到的,一个更为灵活的方法是多阶段设计,对分配比 进行调整,使之有利于本阶段表现得好的一翼。本方法亦适用于结果非二值的情形。一些研 究人员认为这样设计的试验对病人和公益监督委员会(IRB)更为有益。
, 百拇医药
[作者简介] 张学中(1938-),男,教授。研究方向:药品临床试 验统计方法,实验设计与分析。联系电话:(010)68220831。
[参考文献]
[1] E9 Statistical Principles for Clinical Trials[S/OL],http://www. fda.gov/cder/guidance/index.htm,Effective September 16, 1998.
[2] North PM.Ensuring good statistical practice in clinical research:cuidelin es for standard operating procedures(an update),Drug Inf J,1998,32∶665-682.
[3] Marc Buyse.Randomized designs for early trials of new cancer treatments-a n overview[J].Drug Inf J,2000,34∶387-396.
, 百拇医药
[4] Pocock SJ.Clinical trials,a practical approach[M].John Wiley & Son s Ltd.1983,66-89.
[5] Steven Piantadosi.Clinical trials,a methodologic Perspective[M ].New York :John Wiley & Sons,1997.203-229.
[6] Hoel,DG,Sobel M,Weiss GH.A survey of adaptive sampling for clinical t rials[M]. In: RM. Elashoff (Ed.), Perspectives in Biometrics. New York: Acade mic Press,1975.
[7] 汤旦林.医学统计学基础[M].北京:人民卫生出版社,1989.25-27.
收稿:s, 百拇医药