多叶准直器射野处方剂量的快速计算
作者:戴建荣 胡逸民 杨勇
单位:北京,中国医学科学院中国协和医科大学肿瘤医院放射治疗科 100021
关键词:多叶准直器;不规则射野;处方剂量
中华放射肿瘤学杂志000216 【摘要】 目的 建立一种计算多叶准直器(MLC)不规则射野处方剂量的快速方法。方法 考虑到MLC射野的边缘是台阶状、叶片位置坐标可以由治疗计划系统或与MLC配套的叶片位置产生器打印输出这两个特点, 首先由叶片位置坐标计算出射野周长和面积, 然后由面积周长比法计算出不规则野的等效方野边长, 最后按照处理常规方野的方法计算处方剂量。 结果 作为例子, 计算了采用SSD技术的全脑全脊髓照射野和采用SAD技术的鼻咽癌面颈联合野的处方剂量。结论 这种方法适合于靶区参考点位于射野中心区域未被遮挡的情况。与Clarkson积分等其它方法相比, 它具有快速简单的特点。
, 百拇医药
Rapid calculation of the monitor units for multileaf collimator shaped irregular fields
DAI Jianrong HU Yimin YANG Yong
(Department of Radiation Oncology, Cancer Hospital, Chinese Academy of Medical Sciences, Peking Union Medical College, Beijig 100021,China)
【Abstract】 Objective To develop a rapid algorithm in the calculaton of machine monitor units for irregular fields shaped by multileaf collimator (MLC). Methods On considering that the fields' edges are stepwise and the leaves' coordinates can be printed out by a treatment planning system or outlined by a MLC shaper, their area and perimeter can be directly calculated from leaves' coordinates. Then the equivalent field size can be calculated with methods based on the area/perimeter ratio. Finally, the monitor units can be determined from a well-known formula. Results As examples, the total brain-spinal cord field, which was delivered with nominal SSD technique, and head-neck field, which was delivered with SAD technique, were calculated. Conclusions This algorithm is suitable to the situation when the reference point of target dose is located at the central part of a field and has not been blocked. It is quicker and simpler as compared with the other methods such as Clarkson integration.
, 百拇医药
【Key words】 Multileaf collimator;Irregular field;Monitor unit calculation
多叶准直器(multileaf collimator, MLC)的一个重要功能是用来代替挡块,形成适合靶区形状的不规则射野。 对于加速器, 处方剂量是经输出量校正后的机器跳数。 计算MLC形成的不规则射野的处方剂量可以按挡块形成的不规则射野处理, 即可以采用面积周长比、Clarkson积分等方法。 考虑到MLC射野的边缘是台阶状、叶片位置坐标可以由治疗计划系统或与MLC配套的叶片位置产生器打印输出这两个特点, 作者设计了一种基于面积周长比法,适合MLC射野的处方剂量计算方法。 与Clarkson积分等其它方法相比, 这种方法具有快速简单的特点。
1 材料与方法
1.1 MLC射野坐标刻度方法:对于MLC射野, 不规则射野是由所有叶片的位置决定的。 这些叶片位置不是叶片相对于准直器轴线的实际位移, 而是叶片在等中心平面的投影相对于准直器轴线的位移。如果一个多叶准直器有n对叶片, 则说明一个MLC射野需要2n个叶片位置参数。 按照国际电工委员会(international electrotechnical commission, IEC) 1217号标准的规定(见文献[1]), MLC叶片沿射野坐标系的X轴方向运动, 叶片对的编号从Y轴的负方向开始, 依次为1、2、…、n-1、n, 安装在X轴负侧的叶片位置坐标依次用符号X11、X12、…、X1(n-1)、X1n表示, 安装在X轴正侧的叶片位置坐标依次用符号X21、X22、…、X2(n-1)、X2n表示。 当一个叶片位于X轴正侧时,叶片位置为正,否则为负。 因此在等中心平面内, 每一对叶片的开口大小是Fxi=X2i-X1i, 其中i是叶片对的编号(见图1)。
, http://www.100md.com
图1 IEC 1217号标准中规定的MLC射野坐标刻度方法
(从机头方向观察)
目前一些加速器厂家的MLC坐标刻度方法与IEC的规定不一致,主要差别是在这些坐标刻度方法中,规定当一个叶片未越过准直器轴线时,叶片位置为正,否则为负。 不难看出, 在两种规定中, 安装在坐标轴正侧的叶片位置坐标值是相同的, 而安装在坐标轴负侧的叶片位置坐标值刚好相反。 下面介绍的内容均遵照了IEC 1217号标准的规定。 如果读者单位的加速器坐标刻度没有遵照这个规定, 一些公式可能要做相应的修改。
1.2 适合MLC射野的面积周长比法:MLC射野的宽和长是指正好包括MLC形成的不规则射野的矩形的宽和长。 根据X1i不等于X2i的判断条件, 可以找出第一对和最后一对打开的叶片。 设它们的序号分别用s和e表示, 则MLC射野的宽和长可分别表示为
, http://www.100md.com
Fx=max(X2s,X2(S+1),…,X2e)-min(X1S,X1(S+1),…,X1e), (1)
Fy=(e-s+1)W, (2)
其中Fx和Fy 是MLC射野的宽和长, max是求最大值函数, min是求最小值函数,W是叶片在等中心平面的投影宽度。MLC射野的面积是所有打开的叶片对照射范围的总和, 而每一叶片对的照射范围是一个长度为两个叶片位置坐标之差,宽度为W的窄矩形, 故总的射野面积是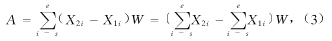 (3)
(3)
(3) 式说明, 只需将X轴正侧的叶片位置坐标之和减去X轴负侧的叶片位置坐标之和, 再乘以叶片宽度就是MLC射野的面积。
, 百拇医药
从数学观点看,MLC射野的周长是指其台阶状边缘的总长。但在采用面积周长比法计算处方剂量时,我们应取与MLC射野对应的挡块野周长。由于MLC射野边缘是台阶状的,而挡块野的边缘是连续的,当用挡块或MLC来形成同一个射野形状时,这个射野的面积近似保持不变,但它的周长可能会有差别。挡块野周长总是小于或等于MLC射野的周长。以一个正方形射野为例,挡块野周长等于正方形周长,而MLC射野周长与MLC叶片的布置方向有关。当MLC叶片平行正方形某一条边布置时,MLC射野周长等于正方形周长;当MLC叶片平行正方形某一条对角线布置时,MLC射野周长等于正方形周长的1.4倍;当MLC叶片沿其它方向布置时,MLC射野周长将介于正方形周长和它的1.4倍之间。挡块野周长可采用连接MLC射野台阶状边缘中点的方法得到,即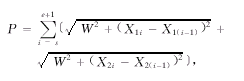 (4)
(4)
其中,当i=s-1时,X1(s-1)=X2(s-1)=(X1s+X2s)/2;当i=e+1时,X1(e+1)=X2(e+1)=(X1e+X2e)/2。
, http://www.100md.com
将面积和周长的计算结果代入面积周长比法的等效野公式, 即可计算出等效方野边长, 即
FSZ=4A/P。 (5)
公式(5)得出的等效方野边长是在等中心平面内的值, 如果采用非标称SSD照射技术, 射野的等效方野边长还需乘比例因子(SSD/SAD)。当等效方野边长确定后, 就可以按照处理常规野的方法计算处方剂量。 根据文献[2]的论述, 当采用SSD照射技术时, 处方剂量的计算公式见公式(6)。其中MU是处方剂量,DT是靶区剂量, PDD是百分深度量, Sc是准直器散射因子,Sp是体模散射因子, Wf是楔形因子, Tf是挡块托架因子, SSD因子是距离平方反比修正因子。当采用SAD照射技术, 处方剂量的计算公式见公式(7)。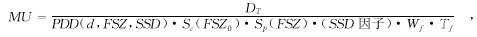 (6)
(6)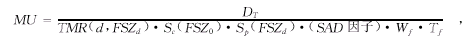 (7)
(7)
, http://www.100md.com
其中TMR是组织最大比, SAD因子是距离平方反比修正因子, 其它符号的含义与(6) 式相同。
设机器输出量校正时源到电离室的距离是SCD, 则SSD因子和SAD因子可分别表示为
SSD因子=[SCD/(SSD+dm)]2, (8)
SAD因子=[SCD/SAD]2。 (9)
本科机器输出量校正时采用了标称SSD照射技术,射野10cm×10cm,电离室位于深度为dm的位置,因此有SCD=标称SSD+dm=SAD+dm。
2 结果
作者对全脑全脊髓照射野和鼻咽癌面颈联合野进行了计算。并假设治疗是在Varian 600C加速器上进行的, 射线是6MV X射线。 MLC由40对叶片组成, 叶片宽度是1.0cm。
, http://www.100md.com
例1. 全脑全脊髓照射野
采用标称SSD照射技术。 射野形状和叶片位置坐标见图2 a。 靶区参考点位于射野中心轴上,深度9cm。 要求靶区剂量给到90cGy, 问所需照射的机器跳数
由图2 a看出, 打开的叶片对范围是14~31, 即s=14, e=31。 将叶片的位置坐标代入(3)式, 得射野面积A=186.7cm2;代入(4)式得射野周长P=58.2cm,故等效方野边长FSZ=12.8cm。查PDD表得 PDD(9.0, 12.8)= 0.708, Sp(12.8)= 1.008。由(1) 式和(2) 式得MLC射野的宽和长分别是 Fx=17.4cm,Fy=18.0cm 。Varian加速器的MLC是安装在二级准直器下方的原挡块托架位置。 在实际使用中, 二级准直器的叶片总是跟随着MLC叶片运动, 二级准直器形成的射野总是刚好包括或稍大于不规则的MLC射野, 以便减少MLC叶片间的漏射线对患者的照射。 由于MLC叶片的介入, 基本上不会减少可以照到靶区参考点的机头散射线的注量, 因此可以认为准直器散射因子是由二级准直器射野决定的, 与MLC叶片位置无关。 假设二级准直器射野的宽和长均是18.0cm, 则查表得准直器散射因子Sc(18.0)= 1.014 。处方剂量公式(11)中的其它项 SSD因子=1.0, Tf= 1.0, Wf=1.0, 将相应的参数值代入,得所需照射的机器跳数为124 。
, 百拇医药
图2 MLC射野示意例2. 鼻咽癌面颈联合野
采用SAD照射技术。 射野形状是由MLC确定的(见图2 b)。 靶区参考点位于等中心, 深度7.0cm。 要求靶区剂量给到100cGy, 问所需照射的机器跳数
由图2 b看出, 打开的叶片对范围是15~28, 即s=15, e=28。 将相应的参数值代入(3)式, 得射野面积A=99.7cm2。代入(4)式得射野周长P=46.2cm。故等效方野边长FSZ=8.6cm 。查TMR表得TMR(7.0, 8.6)= 0.847, Sp(8.6)= 0.999。由(1) 式和(2) 式得MLC射野的宽和长分别是 Fx=11.2cm , Fy=14.0cm。与例1类似, 假设二级准直器射野的宽和长分别是12.0cm和14.0cm, 则等效方野边长FSZ0= 12.9cm, 查表得准直器散射因子Sc(12.9)= 1.006 。处方剂量公式(7)中的其它项SAD因子=1.030, Tf= 1.0, Wf=1.0 , 将相应的参数值代入,得所需照射的机器跳数为114。
, http://www.100md.com
3 讨论
对于MLC射野, 采用本文介绍的方法可以很快地确定等效方野边长, 继而可以按照处理常规野的方法计算处方剂量。 如果采用Clarkson积分法, 首先需要划分扇形, 一般是每10°一个扇形, 然后是测量每1个小扇形的半径, 最后是计算36个小扇形区的剂量贡献, 仅最后一步的计算量就至少相当于36个常规野。 因此,就计算速度而言, 本文介绍的方法要比Clarkson积分法快。 但是, 本文介绍的方法是基于面积周长比法的, 它没有考虑靶区参考点在MLC射野中的位置, 这间接表明了它作了靶区参考点位于射野中心的假设。 因此它只适合靶区参考点位于射野中心区域未被遮挡的情况。 对于这种情况, Lombardi氏等[3]采用面积周长比法和Clarkson积分法计算了40个不规则野的处方剂量, 通过与实验测量结果比较,发现两种方法均有大约3/4的射野的处方剂量误差<1%, 面积周长比法的最大误差是-3.0%, Clarkson积分法的最大误差是-2.8%。 因此,可以认为两种方法的精确度没有差别。 当靶区参考点位于射野边缘或挡块遮挡区域时, 依然需要采用Clarkson积分等其它方法。
, http://www.100md.com
MLC在加速器机头内有3种安装方式: (1)将MLC安装在二级准直器下方的原挡块托架位置, 如Varian公司的; (2)用MLC代替二级准直器的离源较近的一对叶片, 如Philips公司的; (3)用MLC代替二级准直器的离源较远的一对叶片, 如Siemens公司的[4]。 对于第1种安装方式, 在结果部分的例1中已经提到, 可以不考虑MLC对准直器散射因子的影响。对于第2种安装方式, Yuen等[5]的实验表明,准直器散射因子近似由MLC决定,因此可根据(5)式计算等效方野边长,查表得到Sc的值。对于第3种安装方式可采用Kim等[6,7]介绍的基于等效野概念的方法。它包括两个步骤: (1)将视点置于探测器位置观察(detector's eye view, DEV), 确定X线靶所在平面内既没有被MLC叶片遮挡,也没有被二级准直器挡块遮挡的区域, 这个区域称为靶平面投影野;(2)如果靶平面投影野形状是规则的, 则它可直接通过几何关系映射为探测器位置平面的一个等效方野, 前者的准直器散射因子等于后者的; 如果靶平面投影野形状是不规则的, 可采用本文介绍的方法或Clarkson方法计算靶平面投影野的等效方野,然后,通过几何关系映射为探测器位置平面的一个等效方野。
, http://www.100md.com
本文介绍了一种计算MLC射野处方剂量的方法。它基于面积周长比法,适合于靶区参考点位于射野中心区域未被遮挡的情况。与Clarkson积分等其它方法相比, 它具有快速简单的特点。
参 考 文 献
1,International Electrochincal Commission. IEC 1217.
2,胡逸民. 剂量计算举例. 见: 胡逸民, 张红志,戴建荣, 编著. 肿瘤放射物理学, 北京: 原子能出版社, 1999.178-182.
3,Lombardi P, Fiorino C, Cattaneo GM, et al. Monitor unit calculation in 6 MV irregularly shaped beams-accuracy in clinical practice. Br J Radiol, 1997, 70:645-649.
, 百拇医药
4,胡逸民. 多叶准直器. 见: 胡逸民, 张红志,戴建荣, 编著. 肿瘤放射物理学. 北京: 原子能出版社,1999.123-133.
5,Yuan K, AI_Ghazi MSAL, Swift CL, et al .A practical method for the calculation of multileaf collimator shaped fields output factors. Med Phys, 1999, 26:2385-2389.
6,Kim S, Palta JR, Zhu TC. A generalized solution for the calculation of in-air output factors in irregular fields. Med Phys, 1998, 25:1692-1701.
7,Kim S, Zhu TC, Palta JR. An equivalent square field formula for determining head scatter factors of rectangular fields. Med Phys, 1997, 24:1770-1774.
(收稿日期:1999-04-24)
, http://www.100md.com
单位:北京,中国医学科学院中国协和医科大学肿瘤医院放射治疗科 100021
关键词:多叶准直器;不规则射野;处方剂量
中华放射肿瘤学杂志000216 【摘要】 目的 建立一种计算多叶准直器(MLC)不规则射野处方剂量的快速方法。方法 考虑到MLC射野的边缘是台阶状、叶片位置坐标可以由治疗计划系统或与MLC配套的叶片位置产生器打印输出这两个特点, 首先由叶片位置坐标计算出射野周长和面积, 然后由面积周长比法计算出不规则野的等效方野边长, 最后按照处理常规方野的方法计算处方剂量。 结果 作为例子, 计算了采用SSD技术的全脑全脊髓照射野和采用SAD技术的鼻咽癌面颈联合野的处方剂量。结论 这种方法适合于靶区参考点位于射野中心区域未被遮挡的情况。与Clarkson积分等其它方法相比, 它具有快速简单的特点。
, 百拇医药
Rapid calculation of the monitor units for multileaf collimator shaped irregular fields
DAI Jianrong HU Yimin YANG Yong
(Department of Radiation Oncology, Cancer Hospital, Chinese Academy of Medical Sciences, Peking Union Medical College, Beijig 100021,China)
【Abstract】 Objective To develop a rapid algorithm in the calculaton of machine monitor units for irregular fields shaped by multileaf collimator (MLC). Methods On considering that the fields' edges are stepwise and the leaves' coordinates can be printed out by a treatment planning system or outlined by a MLC shaper, their area and perimeter can be directly calculated from leaves' coordinates. Then the equivalent field size can be calculated with methods based on the area/perimeter ratio. Finally, the monitor units can be determined from a well-known formula. Results As examples, the total brain-spinal cord field, which was delivered with nominal SSD technique, and head-neck field, which was delivered with SAD technique, were calculated. Conclusions This algorithm is suitable to the situation when the reference point of target dose is located at the central part of a field and has not been blocked. It is quicker and simpler as compared with the other methods such as Clarkson integration.
, 百拇医药
【Key words】 Multileaf collimator;Irregular field;Monitor unit calculation
多叶准直器(multileaf collimator, MLC)的一个重要功能是用来代替挡块,形成适合靶区形状的不规则射野。 对于加速器, 处方剂量是经输出量校正后的机器跳数。 计算MLC形成的不规则射野的处方剂量可以按挡块形成的不规则射野处理, 即可以采用面积周长比、Clarkson积分等方法。 考虑到MLC射野的边缘是台阶状、叶片位置坐标可以由治疗计划系统或与MLC配套的叶片位置产生器打印输出这两个特点, 作者设计了一种基于面积周长比法,适合MLC射野的处方剂量计算方法。 与Clarkson积分等其它方法相比, 这种方法具有快速简单的特点。
1 材料与方法
1.1 MLC射野坐标刻度方法:对于MLC射野, 不规则射野是由所有叶片的位置决定的。 这些叶片位置不是叶片相对于准直器轴线的实际位移, 而是叶片在等中心平面的投影相对于准直器轴线的位移。如果一个多叶准直器有n对叶片, 则说明一个MLC射野需要2n个叶片位置参数。 按照国际电工委员会(international electrotechnical commission, IEC) 1217号标准的规定(见文献[1]), MLC叶片沿射野坐标系的X轴方向运动, 叶片对的编号从Y轴的负方向开始, 依次为1、2、…、n-1、n, 安装在X轴负侧的叶片位置坐标依次用符号X11、X12、…、X1(n-1)、X1n表示, 安装在X轴正侧的叶片位置坐标依次用符号X21、X22、…、X2(n-1)、X2n表示。 当一个叶片位于X轴正侧时,叶片位置为正,否则为负。 因此在等中心平面内, 每一对叶片的开口大小是Fxi=X2i-X1i, 其中i是叶片对的编号(见图1)。

, http://www.100md.com
图1 IEC 1217号标准中规定的MLC射野坐标刻度方法
(从机头方向观察)
目前一些加速器厂家的MLC坐标刻度方法与IEC的规定不一致,主要差别是在这些坐标刻度方法中,规定当一个叶片未越过准直器轴线时,叶片位置为正,否则为负。 不难看出, 在两种规定中, 安装在坐标轴正侧的叶片位置坐标值是相同的, 而安装在坐标轴负侧的叶片位置坐标值刚好相反。 下面介绍的内容均遵照了IEC 1217号标准的规定。 如果读者单位的加速器坐标刻度没有遵照这个规定, 一些公式可能要做相应的修改。
1.2 适合MLC射野的面积周长比法:MLC射野的宽和长是指正好包括MLC形成的不规则射野的矩形的宽和长。 根据X1i不等于X2i的判断条件, 可以找出第一对和最后一对打开的叶片。 设它们的序号分别用s和e表示, 则MLC射野的宽和长可分别表示为
, http://www.100md.com
Fx=max(X2s,X2(S+1),…,X2e)-min(X1S,X1(S+1),…,X1e), (1)
Fy=(e-s+1)W, (2)
其中Fx和Fy 是MLC射野的宽和长, max是求最大值函数, min是求最小值函数,W是叶片在等中心平面的投影宽度。MLC射野的面积是所有打开的叶片对照射范围的总和, 而每一叶片对的照射范围是一个长度为两个叶片位置坐标之差,宽度为W的窄矩形, 故总的射野面积是
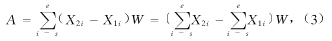 (3)
(3)(3) 式说明, 只需将X轴正侧的叶片位置坐标之和减去X轴负侧的叶片位置坐标之和, 再乘以叶片宽度就是MLC射野的面积。
, 百拇医药
从数学观点看,MLC射野的周长是指其台阶状边缘的总长。但在采用面积周长比法计算处方剂量时,我们应取与MLC射野对应的挡块野周长。由于MLC射野边缘是台阶状的,而挡块野的边缘是连续的,当用挡块或MLC来形成同一个射野形状时,这个射野的面积近似保持不变,但它的周长可能会有差别。挡块野周长总是小于或等于MLC射野的周长。以一个正方形射野为例,挡块野周长等于正方形周长,而MLC射野周长与MLC叶片的布置方向有关。当MLC叶片平行正方形某一条边布置时,MLC射野周长等于正方形周长;当MLC叶片平行正方形某一条对角线布置时,MLC射野周长等于正方形周长的1.4倍;当MLC叶片沿其它方向布置时,MLC射野周长将介于正方形周长和它的1.4倍之间。挡块野周长可采用连接MLC射野台阶状边缘中点的方法得到,即
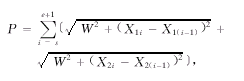 (4)
(4)其中,当i=s-1时,X1(s-1)=X2(s-1)=(X1s+X2s)/2;当i=e+1时,X1(e+1)=X2(e+1)=(X1e+X2e)/2。
, http://www.100md.com
将面积和周长的计算结果代入面积周长比法的等效野公式, 即可计算出等效方野边长, 即
FSZ=4A/P。 (5)
公式(5)得出的等效方野边长是在等中心平面内的值, 如果采用非标称SSD照射技术, 射野的等效方野边长还需乘比例因子(SSD/SAD)。当等效方野边长确定后, 就可以按照处理常规野的方法计算处方剂量。 根据文献[2]的论述, 当采用SSD照射技术时, 处方剂量的计算公式见公式(6)。其中MU是处方剂量,DT是靶区剂量, PDD是百分深度量, Sc是准直器散射因子,Sp是体模散射因子, Wf是楔形因子, Tf是挡块托架因子, SSD因子是距离平方反比修正因子。当采用SAD照射技术, 处方剂量的计算公式见公式(7)。
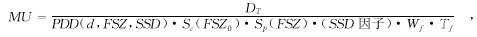 (6)
(6)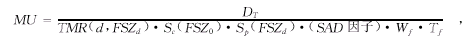 (7)
(7), http://www.100md.com
其中TMR是组织最大比, SAD因子是距离平方反比修正因子, 其它符号的含义与(6) 式相同。
设机器输出量校正时源到电离室的距离是SCD, 则SSD因子和SAD因子可分别表示为
SSD因子=[SCD/(SSD+dm)]2, (8)
SAD因子=[SCD/SAD]2。 (9)
本科机器输出量校正时采用了标称SSD照射技术,射野10cm×10cm,电离室位于深度为dm的位置,因此有SCD=标称SSD+dm=SAD+dm。
2 结果
作者对全脑全脊髓照射野和鼻咽癌面颈联合野进行了计算。并假设治疗是在Varian 600C加速器上进行的, 射线是6MV X射线。 MLC由40对叶片组成, 叶片宽度是1.0cm。
, http://www.100md.com
例1. 全脑全脊髓照射野
采用标称SSD照射技术。 射野形状和叶片位置坐标见图2 a。 靶区参考点位于射野中心轴上,深度9cm。 要求靶区剂量给到90cGy, 问所需照射的机器跳数
由图2 a看出, 打开的叶片对范围是14~31, 即s=14, e=31。 将叶片的位置坐标代入(3)式, 得射野面积A=186.7cm2;代入(4)式得射野周长P=58.2cm,故等效方野边长FSZ=12.8cm。查PDD表得 PDD(9.0, 12.8)= 0.708, Sp(12.8)= 1.008。由(1) 式和(2) 式得MLC射野的宽和长分别是 Fx=17.4cm,Fy=18.0cm 。Varian加速器的MLC是安装在二级准直器下方的原挡块托架位置。 在实际使用中, 二级准直器的叶片总是跟随着MLC叶片运动, 二级准直器形成的射野总是刚好包括或稍大于不规则的MLC射野, 以便减少MLC叶片间的漏射线对患者的照射。 由于MLC叶片的介入, 基本上不会减少可以照到靶区参考点的机头散射线的注量, 因此可以认为准直器散射因子是由二级准直器射野决定的, 与MLC叶片位置无关。 假设二级准直器射野的宽和长均是18.0cm, 则查表得准直器散射因子Sc(18.0)= 1.014 。处方剂量公式(11)中的其它项 SSD因子=1.0, Tf= 1.0, Wf=1.0, 将相应的参数值代入,得所需照射的机器跳数为124 。

, 百拇医药
图2 MLC射野示意例2. 鼻咽癌面颈联合野
采用SAD照射技术。 射野形状是由MLC确定的(见图2 b)。 靶区参考点位于等中心, 深度7.0cm。 要求靶区剂量给到100cGy, 问所需照射的机器跳数
由图2 b看出, 打开的叶片对范围是15~28, 即s=15, e=28。 将相应的参数值代入(3)式, 得射野面积A=99.7cm2。代入(4)式得射野周长P=46.2cm。故等效方野边长FSZ=8.6cm 。查TMR表得TMR(7.0, 8.6)= 0.847, Sp(8.6)= 0.999。由(1) 式和(2) 式得MLC射野的宽和长分别是 Fx=11.2cm , Fy=14.0cm。与例1类似, 假设二级准直器射野的宽和长分别是12.0cm和14.0cm, 则等效方野边长FSZ0= 12.9cm, 查表得准直器散射因子Sc(12.9)= 1.006 。处方剂量公式(7)中的其它项SAD因子=1.030, Tf= 1.0, Wf=1.0 , 将相应的参数值代入,得所需照射的机器跳数为114。
, http://www.100md.com
3 讨论
对于MLC射野, 采用本文介绍的方法可以很快地确定等效方野边长, 继而可以按照处理常规野的方法计算处方剂量。 如果采用Clarkson积分法, 首先需要划分扇形, 一般是每10°一个扇形, 然后是测量每1个小扇形的半径, 最后是计算36个小扇形区的剂量贡献, 仅最后一步的计算量就至少相当于36个常规野。 因此,就计算速度而言, 本文介绍的方法要比Clarkson积分法快。 但是, 本文介绍的方法是基于面积周长比法的, 它没有考虑靶区参考点在MLC射野中的位置, 这间接表明了它作了靶区参考点位于射野中心的假设。 因此它只适合靶区参考点位于射野中心区域未被遮挡的情况。 对于这种情况, Lombardi氏等[3]采用面积周长比法和Clarkson积分法计算了40个不规则野的处方剂量, 通过与实验测量结果比较,发现两种方法均有大约3/4的射野的处方剂量误差<1%, 面积周长比法的最大误差是-3.0%, Clarkson积分法的最大误差是-2.8%。 因此,可以认为两种方法的精确度没有差别。 当靶区参考点位于射野边缘或挡块遮挡区域时, 依然需要采用Clarkson积分等其它方法。
, http://www.100md.com
MLC在加速器机头内有3种安装方式: (1)将MLC安装在二级准直器下方的原挡块托架位置, 如Varian公司的; (2)用MLC代替二级准直器的离源较近的一对叶片, 如Philips公司的; (3)用MLC代替二级准直器的离源较远的一对叶片, 如Siemens公司的[4]。 对于第1种安装方式, 在结果部分的例1中已经提到, 可以不考虑MLC对准直器散射因子的影响。对于第2种安装方式, Yuen等[5]的实验表明,准直器散射因子近似由MLC决定,因此可根据(5)式计算等效方野边长,查表得到Sc的值。对于第3种安装方式可采用Kim等[6,7]介绍的基于等效野概念的方法。它包括两个步骤: (1)将视点置于探测器位置观察(detector's eye view, DEV), 确定X线靶所在平面内既没有被MLC叶片遮挡,也没有被二级准直器挡块遮挡的区域, 这个区域称为靶平面投影野;(2)如果靶平面投影野形状是规则的, 则它可直接通过几何关系映射为探测器位置平面的一个等效方野, 前者的准直器散射因子等于后者的; 如果靶平面投影野形状是不规则的, 可采用本文介绍的方法或Clarkson方法计算靶平面投影野的等效方野,然后,通过几何关系映射为探测器位置平面的一个等效方野。
, http://www.100md.com
本文介绍了一种计算MLC射野处方剂量的方法。它基于面积周长比法,适合于靶区参考点位于射野中心区域未被遮挡的情况。与Clarkson积分等其它方法相比, 它具有快速简单的特点。
参 考 文 献
1,International Electrochincal Commission. IEC 1217.
2,胡逸民. 剂量计算举例. 见: 胡逸民, 张红志,戴建荣, 编著. 肿瘤放射物理学, 北京: 原子能出版社, 1999.178-182.
3,Lombardi P, Fiorino C, Cattaneo GM, et al. Monitor unit calculation in 6 MV irregularly shaped beams-accuracy in clinical practice. Br J Radiol, 1997, 70:645-649.
, 百拇医药
4,胡逸民. 多叶准直器. 见: 胡逸民, 张红志,戴建荣, 编著. 肿瘤放射物理学. 北京: 原子能出版社,1999.123-133.
5,Yuan K, AI_Ghazi MSAL, Swift CL, et al .A practical method for the calculation of multileaf collimator shaped fields output factors. Med Phys, 1999, 26:2385-2389.
6,Kim S, Palta JR, Zhu TC. A generalized solution for the calculation of in-air output factors in irregular fields. Med Phys, 1998, 25:1692-1701.
7,Kim S, Zhu TC, Palta JR. An equivalent square field formula for determining head scatter factors of rectangular fields. Med Phys, 1997, 24:1770-1774.
(收稿日期:1999-04-24)
, http://www.100md.com