后房型人工晶体植入的屈光度曲线回归公式设计
作者:徐雯 姚克
单位:310009 杭州,浙江大学附属第二医院眼科中心
关键词:
后房型人工晶体植入的屈光度曲线回归公式设计 徐雯 姚克 SRKⅡ经验回归公式是临床常用的计算人工晶体屈光度的公式,但该公式将总体按眼轴长度的不同分为五个不连续的区间,且国、内外患者的眼轴长度分布有所不同。鉴于SRKⅡ公式的诸局限性,我们对415只眼后房型人工晶体进行回归分析后提出二元三次回归计算法,旨在对更准确地进行人工晶体屈光度的计算提供一新的思路。
一、资料和方法
1.一般资料:本组415只眼后房型人工晶体中,康明人工晶体为263只,Storz的为89只,Pharmacia的为62只。选择标准:(1)术后3个月以上且屈光状态稳定者;(2)矫正远视力≥0.5;(3)无术后并发症。
, http://www.100md.com
2.方法:(1)术后测量:用意大利产JAV 000型角膜曲率仪测角膜屈光力(K)。用美国产Sonomed A-2500型超声仪测轴长(L)及前房深度(C),速度1 550 m/s。用以下公式矫正[1]:
L=1 532/1 550L0+0.44T
C=1 532/1 550C0
(2)回归分析:对N组数据(Ki,Li,Pi)建立二元三次方程并令其误差为极小,求得各系数值,并将这一分析过程编成程序。
二、结果
1.按人工晶体眼术后轴长的不同对415只眼进行分组:分布情况见表1。
, 百拇医药
表1 415只眼人工晶体术后眼轴长度的分布
术后眼轴长度(mm)
眼数
百分比(%)
L<20
1
0.24
20≤L<21
2
0.48
21≤L<22
23
, 百拇医药 5.54
22≤L<24.5
260
62.65
24.5≤L<27
81
19.52
27≤L<28.5
29
6.99
L≥28.5
19
4.58
, 百拇医药
2.利用计算机回归所得的二元三次方程形式如下:
P=B1K′3+B2K′2L′+B3K′L′2+B4L′3+B5K′2+B6K′L′+B7L′2+B8K′+B9L′+B10
K′=K- (
( 为K的总体平均值)
为K的总体平均值)
, 百拇医药
L′=L-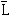 (
(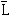 为L的总体平均值)
为L的总体平均值)
不同牌号人工晶体的二元三次回归公式各系数(B1~10)见表2。
表2 3种人工晶体的二元三次回归公式各系数
系数
康明
Storz
Pharmacia
, 百拇医药
B1
-0.174
0.137
0.095
B2
-0.222
0.200
0.093
B3
-0.032
0.054
-0.056
, 百拇医药
B4
-0.035
0.038
-0.010
B5
-0.349
0.179
0.176
B6
-0.100
0.296
0.051
, http://www.100md.com
B7
0.132
0.058
0.005
B8
-0.903
-1.093
-1.018
B9
-1.866
-2.980
-2.510
, 百拇医药
B10
16.308
16.441
16.899
利用二元三次回归公式计算人工晶体屈光度的总体标准差分别为:康明1.60,Storz 1.56,Pharmacia 1.41。均小于利用SRKⅡ公式计算所得的总体标准差,分别为康明1.77,Storz 1.96, Pharmacia 1.79。
三、讨论
目前,临床上常用SRKⅡ公式计算人工晶体植入术中所需植入的后房型人工晶体的屈光度。该公式为一线性回归方程,按轴长将总体分为五个区间。我们通过对415只后房型人工晶体眼轴长度分布的分析发现,长轴眼(L≥24.5 mm)占总体的31.08%,要比国外报道[2]的长轴眼比例(17.0%)高得多,其中重度长轴眼(L>28.5 mm)占4.58%,亦高于西方患者的比例(0.1%)。由此可见,国内患者眼轴长度的总体分布与欧美人种有所不同。在SRKⅡ公式中将长轴眼的部分笼统合并为L≥24.5 mm的分段方法虽适用于欧美人种的眼球,但未必适合于国内患者。另外,人眼的各生物参数包括晶体屈光度P的分布应是连续的,但SRKⅡ公式中,P值在轴长的五个区间之间并不连续,以一不连续的函数来描述一连续的分布,在理论上有其局限性。
, http://www.100md.com
我们用计算机回归了二元三次曲线回归公式,并自编程序供临床进行人工晶体屈光度的计算。该公式为一单调递增曲线,这与SRKⅡ公式相似,但在分布上呈连续性,因此避免了SRKⅡ公式的局限性。经统计分析证实,利用二元三次公式计算的总体标准差小于SRKⅡ公式的总体标准差。该公式虽然形式看似复杂,但在实际应用中将角膜屈光力值和眼轴长度值输入电脑即可得出结果,因此并未增加临床医生的工作负担。 参考文献
1 Holladay JT, Prager TC. Accurate ultrasonic biometry in pseudophakia. Am J Ophthalmol, 1989,107:189-190.
2 Sanders DR, Retzlaff JA, Kraff MC,et al. Comparison of the SRK/T formula and other theoretical and regression formulas. J Cataract Refract Surg, 1990, 16: 341-346.
(收稿:1998-09-15 修回1998-11-30), 百拇医药
单位:310009 杭州,浙江大学附属第二医院眼科中心
关键词:
后房型人工晶体植入的屈光度曲线回归公式设计 徐雯 姚克 SRKⅡ经验回归公式是临床常用的计算人工晶体屈光度的公式,但该公式将总体按眼轴长度的不同分为五个不连续的区间,且国、内外患者的眼轴长度分布有所不同。鉴于SRKⅡ公式的诸局限性,我们对415只眼后房型人工晶体进行回归分析后提出二元三次回归计算法,旨在对更准确地进行人工晶体屈光度的计算提供一新的思路。
一、资料和方法
1.一般资料:本组415只眼后房型人工晶体中,康明人工晶体为263只,Storz的为89只,Pharmacia的为62只。选择标准:(1)术后3个月以上且屈光状态稳定者;(2)矫正远视力≥0.5;(3)无术后并发症。
, http://www.100md.com
2.方法:(1)术后测量:用意大利产JAV 000型角膜曲率仪测角膜屈光力(K)。用美国产Sonomed A-2500型超声仪测轴长(L)及前房深度(C),速度1 550 m/s。用以下公式矫正[1]:
L=1 532/1 550L0+0.44T
C=1 532/1 550C0
(2)回归分析:对N组数据(Ki,Li,Pi)建立二元三次方程并令其误差为极小,求得各系数值,并将这一分析过程编成程序。
二、结果
1.按人工晶体眼术后轴长的不同对415只眼进行分组:分布情况见表1。
, 百拇医药
表1 415只眼人工晶体术后眼轴长度的分布
术后眼轴长度(mm)
眼数
百分比(%)
L<20
1
0.24
20≤L<21
2
0.48
21≤L<22
23
, 百拇医药 5.54
22≤L<24.5
260
62.65
24.5≤L<27
81
19.52
27≤L<28.5
29
6.99
L≥28.5
19
4.58
, 百拇医药
2.利用计算机回归所得的二元三次方程形式如下:
P=B1K′3+B2K′2L′+B3K′L′2+B4L′3+B5K′2+B6K′L′+B7L′2+B8K′+B9L′+B10
K′=K-
, 百拇医药
L′=L-
不同牌号人工晶体的二元三次回归公式各系数(B1~10)见表2。
表2 3种人工晶体的二元三次回归公式各系数
系数
康明
Storz
Pharmacia
, 百拇医药
B1
-0.174
0.137
0.095
B2
-0.222
0.200
0.093
B3
-0.032
0.054
-0.056
, 百拇医药
B4
-0.035
0.038
-0.010
B5
-0.349
0.179
0.176
B6
-0.100
0.296
0.051
, http://www.100md.com
B7
0.132
0.058
0.005
B8
-0.903
-1.093
-1.018
B9
-1.866
-2.980
-2.510
, 百拇医药
B10
16.308
16.441
16.899
利用二元三次回归公式计算人工晶体屈光度的总体标准差分别为:康明1.60,Storz 1.56,Pharmacia 1.41。均小于利用SRKⅡ公式计算所得的总体标准差,分别为康明1.77,Storz 1.96, Pharmacia 1.79。
三、讨论
目前,临床上常用SRKⅡ公式计算人工晶体植入术中所需植入的后房型人工晶体的屈光度。该公式为一线性回归方程,按轴长将总体分为五个区间。我们通过对415只后房型人工晶体眼轴长度分布的分析发现,长轴眼(L≥24.5 mm)占总体的31.08%,要比国外报道[2]的长轴眼比例(17.0%)高得多,其中重度长轴眼(L>28.5 mm)占4.58%,亦高于西方患者的比例(0.1%)。由此可见,国内患者眼轴长度的总体分布与欧美人种有所不同。在SRKⅡ公式中将长轴眼的部分笼统合并为L≥24.5 mm的分段方法虽适用于欧美人种的眼球,但未必适合于国内患者。另外,人眼的各生物参数包括晶体屈光度P的分布应是连续的,但SRKⅡ公式中,P值在轴长的五个区间之间并不连续,以一不连续的函数来描述一连续的分布,在理论上有其局限性。
, http://www.100md.com
我们用计算机回归了二元三次曲线回归公式,并自编程序供临床进行人工晶体屈光度的计算。该公式为一单调递增曲线,这与SRKⅡ公式相似,但在分布上呈连续性,因此避免了SRKⅡ公式的局限性。经统计分析证实,利用二元三次公式计算的总体标准差小于SRKⅡ公式的总体标准差。该公式虽然形式看似复杂,但在实际应用中将角膜屈光力值和眼轴长度值输入电脑即可得出结果,因此并未增加临床医生的工作负担。 参考文献
1 Holladay JT, Prager TC. Accurate ultrasonic biometry in pseudophakia. Am J Ophthalmol, 1989,107:189-190.
2 Sanders DR, Retzlaff JA, Kraff MC,et al. Comparison of the SRK/T formula and other theoretical and regression formulas. J Cataract Refract Surg, 1990, 16: 341-346.
(收稿:1998-09-15 修回1998-11-30), 百拇医药