曲线拟合检验的新概念——面积拟合度
作者：董玉恒 董天
单位：白求恩医科大学地方病研究所(130021) 董玉恒; 吉林大学数学系(130023) 董天
关键词：
中国卫生统计990524拟合度和拟合优度检验的局限性
它们的计算公式〔1～3〕如下：
曲线的拟合度或称相关指数：
直线回归的检验：
曲线回归的检验：
, 百拇医药
直线回归与曲线回归的比较检验：
这些计算和检验大都是有效和适用的，然而有时也出现错误，也表现出应用上的局限性，请看下面的例子。
这是一组生化指标的例子：
X：4， 6， 8， 12， 24， 48；
Y：1.2471，1.3092，1.3639，1.0669， 1.1266， 0.7312
拟合成直线回归的结果：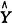
=1.35446-0.0125674X，Σ(Y-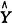)2=0.0408055，拟合度=0.844767
, 百拇医药
直线回归检验F=21.7678，df1=1，df2=4,P=0.0095。
在二到四次多项式的曲线拟合中以四次多项式的拟合度最高(后面将有一到四次多项式曲线拟合的比较)。
拟合成四次多项式曲线回归的结果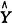：=0.325571+0.375602X-0.0436016X2+
0.001696X3-0.000019731X4，Σ(Y-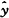
)2=0.00327377，拟合度=0.987546
曲线回归检验F=317.18，df1=1,df2=4,P=0.0001。
, 百拇医药
直线回归与曲线回归的比较：F=12.4644，df1=4,df2=4,P=0.0314。由最后的P值0.0314可以看出曲线比直线效果好得多，但从后面打印结果的图形却看出相反的结果。
显然曲线不如直线，因为观察点都在直线附近。问题的症结就在于曲线的理论点与各观察点的距离比直线近，虽然它的其余部分偏离很远，特别是后面部分偏离更远。这与上面结论恰好相反。为正确全面评价拟合度，我们提出如下设想，作为补充。至于本例究竟应拟合几次曲线，请看下面的比较。
评价曲线拟合度的新设想
笔者认为应该用面积建立度量指标。在面积拟合度的计算中，从几何学的观点，平方和Σ(Y-
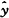)2，Σ(Y-)2中的观察值Y是折线，是平行于X轴的直线，而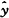是拟合的曲线。因此相当于前者的应为折线与直线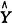=间的面积，相当于后者的应为曲线(包括直线)与折线间的面积。为计算前者，应计算折线和X轴围成的面积与对应区域均数直线和X轴围成的面积之差。折线和X轴围成的面积是多个梯形。这样拟合直线与折线间的面积也就好求了。曲线与折线间的面积将用积分计算。对于这些计算，我们用上述例子作如下说明：
, 百拇医药
为求折线与直线
=间的面积，需逐段计算面积，再相加。对于折线在均数直线之上或之下的情形，只需计算折线和横轴形成的梯形面积与均数直线和横轴形成的矩形面积之差即可；对于折线与均数直线交叉的情形，在交点处分成两部分，只要分别计算两个三角形的面积即可。设交点为jd。这是求由已知两点形成的直线与均数直线间的交点。设两点为(xj,yj),(xj+1,yj+1),当yj+1>yj时有图形：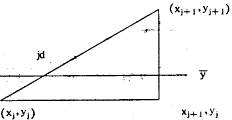
则有：
, 百拇医药
类似地，当yj+1j时，
本例折线与均数直线间面积=6.65285。
计算拟合直线与折线间的面积也是类似的。只是拟合直线与横轴交点的计算问题。如果交点在自变量的范围之外，则只是一个梯形，否则就是两个三角形，交点计算用下式：
本例拟合直线与折线间的面积=0.326339。
为了符合原拟合度的度量习惯，即面积拟合度小于或等于1，越接近1越好，为此用下式表示面积拟合度：
, 百拇医药
求曲线与折线间的面积也是逐段计算，计算方法是逐段计算曲线和X轴间面积与折线和X轴间面积之差。曲线与X轴间面积用
计算，如果整个曲线都在X轴以上，则为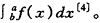
对于其他曲线，不大可能出现上述偏差，因此，我们只讨论多项式曲线的情形，用公式∫xndx=xn+1/(n+1)即可。另外，本例整个曲线都在X轴以上。本例曲线与折线间面积=37.3602。拟合的结果见图1。
图1 面积拟合度图
就此例来说，按通常拟合度，曲线优于直线，而按面积拟合度，直线优于曲线。后面结论正确，下面就把本例拟合成一至四次多项式的结果列于表1作为比较(为区别起见，把原拟合度改称为误差拟合度)：
, 百拇医药
表1 拟合结果比较 曲线次数
估计误差
平方和
误差
拟合度
曲线
面积
面积
拟合度
平均
拟合度
一次
0.0408055
, 百拇医药
0.844767
0.326339
0.950948
0.8978575
二次
0.0393173
0.850429
0.309743
0.953442
0.9019355
三次
0.0360693
, 百拇医药
0.862785
1.80179
0.729171
0.795978
四次
0.00327377
0.987546
37.3602
-4.61567
-1.814062
可以认为，拟合直线为最好。显然，四次曲线是说明此问题的最典型例子，所以本文的开头用它与直线进行比较，上图中拟合的分别是二次和四次抛物线。
参考文献
1.李建立，史秉璋.曲线拟合的样条函数方法探讨.中国卫生统计，1985，2(1)：28.
2.杨树勤.中国医学百科全书*医学统计学.上海：上海科学技术出版社，1985，146，166-167，171.
3.郭祖超.医用数理统计方法.第2版.北京：人民卫生出版社，1965，459.
4.斯米尔诺夫.高等数学教程.第一卷.孙念增译，北京：高等教育出版社，1956，243，251-252., http://www.100md.com
单位：白求恩医科大学地方病研究所(130021) 董玉恒; 吉林大学数学系(130023) 董天
关键词：
中国卫生统计990524拟合度和拟合优度检验的局限性
它们的计算公式〔1～3〕如下：
曲线的拟合度或称相关指数：
直线回归的检验：
曲线回归的检验：
, 百拇医药
直线回归与曲线回归的比较检验：
这些计算和检验大都是有效和适用的，然而有时也出现错误，也表现出应用上的局限性，请看下面的例子。
这是一组生化指标的例子：
X：4， 6， 8， 12， 24， 48；
Y：1.2471，1.3092，1.3639，1.0669， 1.1266， 0.7312
拟合成直线回归的结果：
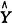=1.35446-0.0125674X，Σ(Y-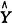)2=0.0408055，拟合度=0.844767, 百拇医药
直线回归检验F=21.7678，df1=1，df2=4,P=0.0095。
在二到四次多项式的曲线拟合中以四次多项式的拟合度最高(后面将有一到四次多项式曲线拟合的比较)。
拟合成四次多项式曲线回归的结果：
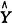=0.325571+0.375602X-0.0436016X2+0.001696X3-0.000019731X4，Σ(Y-
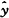)2=0.00327377，拟合度=0.987546曲线回归检验F=317.18，df1=1,df2=4,P=0.0001。
, 百拇医药
直线回归与曲线回归的比较：F=12.4644，df1=4,df2=4,P=0.0314。由最后的P值0.0314可以看出曲线比直线效果好得多，但从后面打印结果的图形却看出相反的结果。
显然曲线不如直线，因为观察点都在直线附近。问题的症结就在于曲线的理论点与各观察点的距离比直线近，虽然它的其余部分偏离很远，特别是后面部分偏离更远。这与上面结论恰好相反。为正确全面评价拟合度，我们提出如下设想，作为补充。至于本例究竟应拟合几次曲线，请看下面的比较。
评价曲线拟合度的新设想
笔者认为应该用面积建立度量指标。在面积拟合度的计算中，从几何学的观点，平方和Σ(Y-
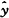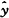)2，Σ(Y-)2中的观察值Y是折线，是平行于X轴的直线，而是拟合的曲线。因此相当于前者的应为折线与直线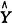=间的面积，相当于后者的应为曲线(包括直线)与折线间的面积。为计算前者，应计算折线和X轴围成的面积与对应区域均数直线和X轴围成的面积之差。折线和X轴围成的面积是多个梯形。这样拟合直线与折线间的面积也就好求了。曲线与折线间的面积将用积分计算。对于这些计算，我们用上述例子作如下说明：, 百拇医药
为求折线与直线
=间的面积，需逐段计算面积，再相加。对于折线在均数直线之上或之下的情形，只需计算折线和横轴形成的梯形面积与均数直线和横轴形成的矩形面积之差即可；对于折线与均数直线交叉的情形，在交点处分成两部分，只要分别计算两个三角形的面积即可。设交点为jd。这是求由已知两点形成的直线与均数直线间的交点。设两点为(xj,yj),(xj+1,yj+1),当yj+1>yj时有图形：则有：
, 百拇医药
类似地，当yj+1
本例折线与均数直线间面积=6.65285。
计算拟合直线与折线间的面积也是类似的。只是拟合直线与横轴交点的计算问题。如果交点在自变量的范围之外，则只是一个梯形，否则就是两个三角形，交点计算用下式：
本例拟合直线与折线间的面积=0.326339。
为了符合原拟合度的度量习惯，即面积拟合度小于或等于1，越接近1越好，为此用下式表示面积拟合度：
, 百拇医药
求曲线与折线间的面积也是逐段计算，计算方法是逐段计算曲线和X轴间面积与折线和X轴间面积之差。曲线与X轴间面积用
计算，如果整个曲线都在X轴以上，则为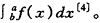对于其他曲线，不大可能出现上述偏差，因此，我们只讨论多项式曲线的情形，用公式∫xndx=xn+1/(n+1)即可。另外，本例整个曲线都在X轴以上。本例曲线与折线间面积=37.3602。拟合的结果见图1。图1 面积拟合度图
就此例来说，按通常拟合度，曲线优于直线，而按面积拟合度，直线优于曲线。后面结论正确，下面就把本例拟合成一至四次多项式的结果列于表1作为比较(为区别起见，把原拟合度改称为误差拟合度)：
, 百拇医药
表1 拟合结果比较 曲线次数
估计误差
平方和
误差
拟合度
曲线
面积
面积
拟合度
平均
拟合度
一次
0.0408055
, 百拇医药
0.844767
0.326339
0.950948
0.8978575
二次
0.0393173
0.850429
0.309743
0.953442
0.9019355
三次
0.0360693
, 百拇医药
0.862785
1.80179
0.729171
0.795978
四次
0.00327377
0.987546
37.3602
-4.61567
-1.814062
可以认为，拟合直线为最好。显然，四次曲线是说明此问题的最典型例子，所以本文的开头用它与直线进行比较，上图中拟合的分别是二次和四次抛物线。
参考文献
1.李建立，史秉璋.曲线拟合的样条函数方法探讨.中国卫生统计，1985，2(1)：28.
2.杨树勤.中国医学百科全书*医学统计学.上海：上海科学技术出版社，1985，146，166-167，171.
3.郭祖超.医用数理统计方法.第2版.北京：人民卫生出版社，1965，459.
4.斯米尔诺夫.高等数学教程.第一卷.孙念增译，北京：高等教育出版社，1956，243，251-252., http://www.100md.com