提高非线性函数近似回归模型预测精度的探讨体外乳酸菌素促双歧杆菌生长实验初步观察体外14C-尿素呼气试验检测胃内幽门螺杆菌感染研究
作者：姚莉 张世强
单位：重庆医科大学数理教研室(400046)
关键词：
中国卫生统计990522 常用非线性函数近似回归模型的求法，通常是采用把非线性函数进行变量代换，转化为线性方程后进行线性回归，然后还原为非线性函数，即曲线直线化的回归方法。该方法在变换过程中，会严重影响到一些非线性函数近似回归模型的预测精度，下面分析产生该问题的原因，并给出解决此问题的方法。
原理与方法
对于n对实测数据{(xi,yi)｜i=1,2,…,n}，倘若它们之间的函数关系是非线性的，但可以通过变量代换Y=f(y)把它们转化为线性关系，就可以用最小二乘法求出它们的近似回归模型。令S1=Σ(yi-
i)2，据文献〔1〕我们得到S1的近似式为
, http://www.100md.com
对S1应用最小二乘原理，求出正规方程后，就可以求出该非线性函数的近似回归模型。该模型对预测精度有何影响呢?从S1=Σ(yi-i)2推出的回归方程y=a+bx为：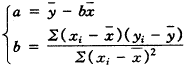
可见参数a、b均受
的影响，特别是a受的影响最大。确是y回归直线的截距。而
显然严重受到数值大的yi的影响。故从S1=Σ(yi-i)2推出的回归模型可视为是对数值大的yi加大权重后得出的。从而可知，用S1=Σ(yi-i)2导出的近似回归模型对于数值大的yi的预测精度高，而对数值小的yi的预测精度低。
, 百拇医药
在解决实际问题时，当关心的重点是较大的yi时，用该方法就能满足要求。反之，当关心的重点是较小的yi时，就必须采用如下的方法来解决。
令
，据文献〔1〕我们可得S2的近似式为
对S2应用最小二乘原理，求出对应的正规方程后，就得到非线性函数的另一近似回归模型。
上面已提到，从S1=Σ(yi-i)2推出的回归模型可视为是对数值大的yi加大权重后得出的。为了削弱S1隐含的对数值大的yi加大权重的影响，把S1每一项除以yi，就可以弱化数值大的yi对S1的影响，强化数值小的yi对S1的影响，从而得到S2=Σ
。由于是每一项除以yi，所以S2实质是对数值小的yi明显加大了权重。即用S2导出的近似回归模型对于数值小的yi的预测值精度高。
, http://www.100md.com
实例分析
某防治站重复治疗钩虫病人的次数与复查阳性率的数据如表1〔2〕。
表1 治疗次数与复查阳性率数据 x
1
2
3
4
5
6
7
8
y
, 百拇医药 63.9
36.0
17.1
10.5
7.3
4.5
2.8
1.7
问题1，预测治疗次数≤4次的病人复查阳性率值。
设非线性模型为y=eA+Bx，变量代换为Y=lny，则
正规方程为
, http://www.100md.com
求得非线性模型为
y1=e4.736-0.583x
问题2，预测治疗次数>4次的病人的复查阳性率值。
正规方程为
求得非线性模型为
y2=e4.526-0.506x
现将预测值与原始值列于表2。
表2 治疗次数与复查阳性率及预测值数据 x
, http://www.100md.com
1
2
3
4
5
6
7
8
y
63.9
36.0
17.1
10.5
7.3
, 百拇医药
4.5
2.8
1.7
y1
63.62
35.5
19.83
11.07
6.18
3.45
1.92
1.07
y2
, http://www.100md.com
55.7
33.58
20.25
12.21
7.36
4.44
2.68
1.61
从表2可以看出，解决问题1采用非线性模型y1较为理想，解决问题2则采用非线性模型y2较为理想。讨 论
提高非线性函数近似回归模型预测精度的最好方法当然是非线性回归法，但该方法对于大多数应用工作者来说，应用起来不方便，有时也不必要，于是寻求一种简单、实用而又能提高预测精度的方法将是有实际意义的。基于应用的目的，本文根据实际需要提出了两种解决问题的方法，它们都可以统称为加权最小二乘法。将它们灵活应用于实际课题中，一定有助于实际问题的解决。
, 百拇医药
参考文献
1.张世强.常用非线性函数模型的新近似回归方法及应用.中国卫生统计，1997，14(1)：20.
2.张成岗，等.利用变量转换及k值修饰进行曲线拟合.中国卫生统计，1994，11(4)：22.
中国微生态学杂志 2000年第5期第12卷 论 著
体外乳酸菌素促双歧杆菌生长实验初步观察
作者：郭思建 戴建红 林敏西 范学工
单位：湖南医科大学附属湘雅医院 检验科，长沙410008
关键词：乳酸菌素；双歧杆菌.
中国微生态学杂志 2000年第5期第12卷 论 著
体外14C-尿素呼气试验检测胃内幽门螺杆菌感染研究
作者：张厚德 曾忠铭 马永健
单位：张厚德(深圳市南山医院消化内科，深圳 518052)；曾忠铭(深圳市南山医院微生态室)；马永健(深圳大学核技术应用联合研究所)
关键词：尿素呼气试验；幽门螺杆菌., http://www.100md.com
单位：重庆医科大学数理教研室(400046)
关键词：
中国卫生统计990522 常用非线性函数近似回归模型的求法，通常是采用把非线性函数进行变量代换，转化为线性方程后进行线性回归，然后还原为非线性函数，即曲线直线化的回归方法。该方法在变换过程中，会严重影响到一些非线性函数近似回归模型的预测精度，下面分析产生该问题的原因，并给出解决此问题的方法。
原理与方法
对于n对实测数据{(xi,yi)｜i=1,2,…,n}，倘若它们之间的函数关系是非线性的，但可以通过变量代换Y=f(y)把它们转化为线性关系，就可以用最小二乘法求出它们的近似回归模型。令S1=Σ(yi-
i)2，据文献〔1〕我们得到S1的近似式为, http://www.100md.com
对S1应用最小二乘原理，求出正规方程后，就可以求出该非线性函数的近似回归模型。该模型对预测精度有何影响呢?从S1=Σ(yi-
i)2推出的回归方程y=a+bx为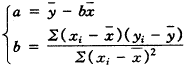：可见参数a、b均受
的影响，特别是a受的影响最大。确是y回归直线的截距。而显然严重受到数值大的yi的影响。故从S1=Σ(yi-i)2推出的回归模型可视为是对数值大的yi加大权重后得出的。从而可知，用S1=Σ(yi-i)2导出的近似回归模型对于数值大的yi的预测精度高，而对数值小的yi的预测精度低。, 百拇医药
在解决实际问题时，当关心的重点是较大的yi时，用该方法就能满足要求。反之，当关心的重点是较小的yi时，就必须采用如下的方法来解决。
令
，据文献〔1〕我们可得S2的近似式为对S2应用最小二乘原理，求出对应的正规方程后，就得到非线性函数的另一近似回归模型。
上面已提到，从S1=Σ(yi-
i)2推出的回归模型可视为是对数值大的yi加大权重后得出的。为了削弱S1隐含的对数值大的yi加大权重的影响，把S1每一项除以yi，就可以弱化数值大的yi对S1的影响，强化数值小的yi对S1的影响，从而得到S2=Σ。由于是每一项除以yi，所以S2实质是对数值小的yi明显加大了权重。即用S2导出的近似回归模型对于数值小的yi的预测值精度高。, http://www.100md.com
实例分析
某防治站重复治疗钩虫病人的次数与复查阳性率的数据如表1〔2〕。
表1 治疗次数与复查阳性率数据 x
1
2
3
4
5
6
7
8
y
, 百拇医药 63.9
36.0
17.1
10.5
7.3
4.5
2.8
1.7
问题1，预测治疗次数≤4次的病人复查阳性率值。
设非线性模型为y=eA+Bx，变量代换为Y=lny，则
正规方程为
, http://www.100md.com
求得非线性模型为
y1=e4.736-0.583x
问题2，预测治疗次数>4次的病人的复查阳性率值。
正规方程为
求得非线性模型为
y2=e4.526-0.506x
现将预测值与原始值列于表2。
表2 治疗次数与复查阳性率及预测值数据 x
, http://www.100md.com
1
2
3
4
5
6
7
8
y
63.9
36.0
17.1
10.5
7.3
, 百拇医药
4.5
2.8
1.7
y1
63.62
35.5
19.83
11.07
6.18
3.45
1.92
1.07
y2
, http://www.100md.com
55.7
33.58
20.25
12.21
7.36
4.44
2.68
1.61
从表2可以看出，解决问题1采用非线性模型y1较为理想，解决问题2则采用非线性模型y2较为理想。讨 论
提高非线性函数近似回归模型预测精度的最好方法当然是非线性回归法，但该方法对于大多数应用工作者来说，应用起来不方便，有时也不必要，于是寻求一种简单、实用而又能提高预测精度的方法将是有实际意义的。基于应用的目的，本文根据实际需要提出了两种解决问题的方法，它们都可以统称为加权最小二乘法。将它们灵活应用于实际课题中，一定有助于实际问题的解决。
, 百拇医药
参考文献
1.张世强.常用非线性函数模型的新近似回归方法及应用.中国卫生统计，1997，14(1)：20.
2.张成岗，等.利用变量转换及k值修饰进行曲线拟合.中国卫生统计，1994，11(4)：22.
中国微生态学杂志 2000年第5期第12卷 论 著
体外乳酸菌素促双歧杆菌生长实验初步观察
作者：郭思建 戴建红 林敏西 范学工
单位：湖南医科大学附属湘雅医院 检验科，长沙410008
关键词：乳酸菌素；双歧杆菌.
中国微生态学杂志 2000年第5期第12卷 论 著
体外14C-尿素呼气试验检测胃内幽门螺杆菌感染研究
作者：张厚德 曾忠铭 马永健
单位：张厚德(深圳市南山医院消化内科，深圳 518052)；曾忠铭(深圳市南山医院微生态室)；马永健(深圳大学核技术应用联合研究所)
关键词：尿素呼气试验；幽门螺杆菌., http://www.100md.com